This is a continuation of the discussion on sequential spaces started with the post Sequential spaces, I and Sequential spaces, II and k-spaces, I. The topology in a sequential space is generated by the convergent sequences. The convergence we are interested in is from a topological view point and not necessarily from a metric (i.e. distance) standpoint. In our discussion, a sequence  converges to
converges to  simply means for each open set
simply means for each open set 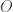 containing
containing  ,
, 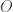 contains
contains 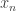 for all but finitely many
for all but finitely many  . In any topological space, there are always trivial convergent sequences. These are sequences of points that are eventually constant, i.e. the sequences
. In any topological space, there are always trivial convergent sequences. These are sequences of points that are eventually constant, i.e. the sequences 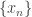 where for some
where for some  ,
, 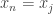 for
for  . Any convergent sequence that is not eventually constant is called a non-trivial convergent sequence. We present an example of a space where there are no non-trivial convergent sequences of points. This space is derived from the Euclidean topology on the real line. This space has no isolated point in this space and yet has no non-trivial convergent sequences and has no infinite compact sets. From this example, we make some observations about sequential spaces and k-spaces.
. Any convergent sequence that is not eventually constant is called a non-trivial convergent sequence. We present an example of a space where there are no non-trivial convergent sequences of points. This space is derived from the Euclidean topology on the real line. This space has no isolated point in this space and yet has no non-trivial convergent sequences and has no infinite compact sets. From this example, we make some observations about sequential spaces and k-spaces.
The space we define here is obtained by modifying the Euclidean topology on the real line. Let  be the real line. Let
be the real line. Let 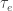 be the Euclidean topology on the real line. Consider the following collection of subsets of the real line:
be the Euclidean topology on the real line. Consider the following collection of subsets of the real line:

It can be verified that  is a base for a topology
is a base for a topology  on
on  . In fact this topology is finer than the Euclidean topology. Denote
. In fact this topology is finer than the Euclidean topology. Denote  with this finer topology by
with this finer topology by  . Clearly
. Clearly  is Hausdorff since the Euclidean topology is. Any countable subset of
is Hausdorff since the Euclidean topology is. Any countable subset of  is closed. Thus
is closed. Thus  is not separable (no countable set can be dense). This space is a handy example of a hereditarily Lindelof space that is not separable. The following lists some properties of
is not separable (no countable set can be dense). This space is a handy example of a hereditarily Lindelof space that is not separable. The following lists some properties of  :
:
 is herditarily Lindelof.
is herditarily Lindelof.- There are no non-trivial convergent sequences in
 .
.
- All compact subsets of
 are finite.
are finite.
 is not a k-space and is thus not sequential.
is not a k-space and is thus not sequential.
Discussion of 1. This follows from the fact that the real line with the Euclidean topology is hereditarily Lindelof and the fact that each open set in  is an Euclidean open set minus a countable set.
is an Euclidean open set minus a countable set.
Discussion of 2 This follows from the fact that every countable subset of  is closed. If a non-trivial sequence
is closed. If a non-trivial sequence 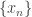 were to converge to
were to converge to 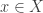 , then
, then 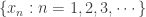 would be a countable subset of
would be a countable subset of  that is not closed.
that is not closed.
Discussion of 3. Let  be an infinite set. If
be an infinite set. If  is bounded in the Euclidean topology, then there would be a non-trivial convergent sequence of points of
is bounded in the Euclidean topology, then there would be a non-trivial convergent sequence of points of  in the Euclidean topology, say,
in the Euclidean topology, say,  . Let
. Let  , which is open in
, which is open in  . For
. For 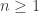 , let
, let 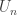 be Euclidean open such that
be Euclidean open such that 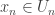 . We also require that all
. We also require that all 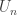 are pairwise disjoint and not contain
are pairwise disjoint and not contain  . Then
. Then 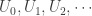 form an open cover of
form an open cover of  (in the topology of
(in the topology of  ) that has no finite subcover. So any bounded infinite
) that has no finite subcover. So any bounded infinite  is not compact in
is not compact in  .
.
Suppose  is unbounded in the Euclidean topology. Then
is unbounded in the Euclidean topology. Then  contains a closed and discrete subset
contains a closed and discrete subset 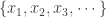 in the Euclidean topology. We can find Euclidean open sets
in the Euclidean topology. We can find Euclidean open sets 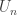 that are pairwise disjoint such that
that are pairwise disjoint such that 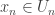 for each
for each  . Let
. Let  , which is open in
, which is open in  . Then
. Then 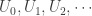 form an open cover of
form an open cover of  (in the topology of
(in the topology of  ) that has no finite subcover. So any unbounded infinite
) that has no finite subcover. So any unbounded infinite  is not compact in
is not compact in  .
.
Discussion of 4. Note that every point of  is a non-isolated point. Just pick any
is a non-isolated point. Just pick any 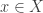 . Then
. Then 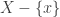 is not closed in
is not closed in  . However, according to 3,
. However, according to 3, 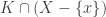 is finite and is thus closed in
is finite and is thus closed in  for every compact
for every compact  . Thus
. Thus  is not a k-space.
is not a k-space.
General Discussion
Suppose  is the topology for the space
is the topology for the space  . Let
. Let 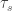 be the set of all sequentially open sets with respect to
be the set of all sequentially open sets with respect to  (see Sequential spaces, II). Let
(see Sequential spaces, II). Let 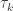 be the set of all compactly generated open sets with respect to
be the set of all compactly generated open sets with respect to  (see k-spaces, I). The space
(see k-spaces, I). The space  is a sequential space (a k-space ) if
is a sequential space (a k-space ) if  (
(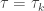 ). Both
). Both 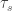 and
and 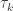 are finer than
are finer than  , i.e.
, i.e. 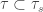 and
and 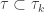 . When are
. When are 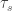 and
and 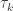 discrete? We discuss sequential spaces and k-spaces separately.
discrete? We discuss sequential spaces and k-spaces separately.
Observations on Sequential Spaces
With respect to the space  , we discuss the following four properties:
, we discuss the following four properties:
- A.
 No non-trivial convergent sequences.
No non-trivial convergent sequences.
- B.

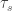 is a discrete topology.
is a discrete topology.
- C.

 is a discrete topology.
is a discrete topology.
- D.
 Sequential, i.e.,
Sequential, i.e.,  .
.
Observation 1
The topology 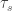 is discrete if and only if
is discrete if and only if  has no non-trivial convergent sequences, i.e.
has no non-trivial convergent sequences, i.e. 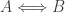 .
.
If 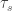 is a discrete topology, then every subset of
is a discrete topology, then every subset of  is sequentially open and every subset is sequentially closed. Hence there can be no non-trivial convergent sequences. If there are no non-trivial convergent sequences, every subset of the space is sequentially closed (thus every subset is sequentially open).
is sequentially open and every subset is sequentially closed. Hence there can be no non-trivial convergent sequences. If there are no non-trivial convergent sequences, every subset of the space is sequentially closed (thus every subset is sequentially open).
Observation 2
Given that  has no non-trivial convergent sequences,
has no non-trivial convergent sequences,  is not discrete if and only if
is not discrete if and only if  is not sequential. Equivalently, given property A,
is not sequential. Equivalently, given property A,  .
.
Given that there are no non-trivial convergent sequences in  ,
, 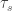 is discrete. For
is discrete. For  to be sequential,
to be sequential,  . Thus for a space
. Thus for a space  that has no non-trivial convergent sequences, the only way for
that has no non-trivial convergent sequences, the only way for  to be sequential is that it is a discrete space.
to be sequential is that it is a discrete space.
Observation 3
Given  is not discrete,
is not discrete,  has no non-trivial convergent sequences implies that
has no non-trivial convergent sequences implies that  is not sequential, i.e. given
is not sequential, i.e. given 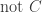 ,
,  . The converse does not hold.
. The converse does not hold.
Observation 3 is a rewording of observation 2. To see that the converse of observation 3 does not hold, consider ![Y=[0,\omega_1]=\omega_1+1](https://s0.wp.com/latex.php?latex=Y%3D%5B0%2C%5Comega_1%5D%3D%5Comega_1%2B1&bg=ffffff&fg=333333&s=0&c=20201002) , the successor ordinal to the first uncountable ordinal with the order topology. It is not sequential as the singleton set
, the successor ordinal to the first uncountable ordinal with the order topology. It is not sequential as the singleton set  is sequentially open and not open.
is sequentially open and not open.
Observations on k-spaces
The discussion on k-spaces mirrors the one on sequential spaces. With respect to the space  , we discuss the following four properties:
, we discuss the following four properties:
- E.
 No infinite compact sets.
No infinite compact sets.
- F.

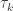 is a discrete topology.
is a discrete topology.
- G.

 is a discrete topology.
is a discrete topology.
- H.
 k-space, i.e.,
k-space, i.e., 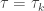 .
.
Observation 4
The topology 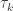 is discrete if and only if
is discrete if and only if  has no infinite compact sets, i.e.
has no infinite compact sets, i.e. 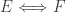 .
.
If 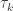 is a discrete topology, then every subset of
is a discrete topology, then every subset of  is a compactly generated open set. In particular, for every compact
is a compactly generated open set. In particular, for every compact 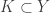 , every subset of
, every subset of  is open in
is open in  . This means
. This means  is discrete and thus must be finite. Hence there can be no infinite compact sets if
is discrete and thus must be finite. Hence there can be no infinite compact sets if 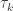 is discrete. If there are no infinite compact sets, every subset of the space is a compactly generated closed set (thus every subset is a compactly generated open set).
is discrete. If there are no infinite compact sets, every subset of the space is a compactly generated closed set (thus every subset is a compactly generated open set).
Observation 5
Given that  has no infinite compact sets,
has no infinite compact sets,  is not discrete if and only if
is not discrete if and only if  is not a k-space. Equivalently, given property E,
is not a k-space. Equivalently, given property E,  .
.
Given that there are no infinite compact sets in  ,
, 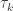 is discrete. For
is discrete. For  to be a k-space,
to be a k-space, 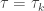 . Thus for a space
. Thus for a space  that has no infinite compact sets, the only way for
that has no infinite compact sets, the only way for  to be a k-space is that it is a discrete space.
to be a k-space is that it is a discrete space.
Observation 6
Given  is not discrete,
is not discrete,  has no infinite compact sets implies that
has no infinite compact sets implies that  is not a k-space, i.e. given
is not a k-space, i.e. given 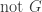 ,
, 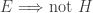 . The converse does not hold.
. The converse does not hold.
Observation 6 is a rewording of observation 5. To see that the converse of observation 6 does not hold, consider the topological sum of a non-k-space and an infinite compact space.
Remark
In the space  defined above by removing countable sets from Euclidean open subsets of the real line, there are no infinite compact sets and no non-trivial convergent sequences. Yet the space is not discrete. Thus it can neither be a sequential space nor a k-space. Another observation we would like to make is that no infinite compact sets implies no non-trivial convergent sequences (
defined above by removing countable sets from Euclidean open subsets of the real line, there are no infinite compact sets and no non-trivial convergent sequences. Yet the space is not discrete. Thus it can neither be a sequential space nor a k-space. Another observation we would like to make is that no infinite compact sets implies no non-trivial convergent sequences (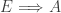 ). However, the converse is not true. Consider
). However, the converse is not true. Consider 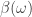 , the Stone-Cech compactification of
, the Stone-Cech compactification of  , the set of all nonnegative integers.
, the set of all nonnegative integers.
Reference
- Engelking, R. General Topology, Revised and Completed edition, 1989, Heldermann Verlag, Berlin.
- Willard, S., General Topology, 1970, Addison-Wesley Publishing Company.
is not sequential). What is more remarkable is that the product of two sequential spaces needs not be sequential. We present an example of a first countable space and a Frechet space whose product is not a k-space (thus not sequential). For the previous discussion on this blog on sequential spaces and k-spaces, see the links at the end of this post.
be the real line and let
be the set of all positive integers. Let
be the space
with the topology inherited from the usual topology on the real line. Let
with the positive integers identified as one point (call this point
). We claim that
is not a k-space and thus not a sequential space. To this end, we define a non-closed
such that
is closed in
for all compact
.
where for each
, the set
is defined by the following:
.
is not closed as
. In fact in the product space
, the point
is the only limit point of the set
. Another observation is that for each
,
is not a limit point of
. Furthermore, if
for each
where
is an infinite subset of
, then
is not a limit point of
. It follows that no infinite subset of
is compact. Consequently,
is finite for each compact
. Thus
is not a k-space. To see that
is not sequential directly, observe that
is sequentially closed.
