Certain covering properties and separation properties allow open covers to shrink, e.g. paracompact spaces, normal spaces, and countably paracompact spaces. The shrinking property is also interesting on its own. This post gives a more in-depth discussion than the one in the previous post on countably paracompact spaces. After discussing shrinking spaces, we introduce three shrinking related properties. These properties show that there is a deep and delicate connection among shrinking properties and normality in products. This post is also a preparation for the next post on  -Dowker space and Morita’s first conjecture.
-Dowker space and Morita’s first conjecture.
All spaces under consideration are Hausdorff and normal or Hausdorff and regular (if not normal).
____________________________________________________________________
Shrinking Spaces
Let  be a space. Let
be a space. Let  be an open cover of
be an open cover of  . The open cover of
. The open cover of  is said to be shrinkable if there is an open cover
is said to be shrinkable if there is an open cover  of
of  such that
such that 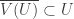 for each
for each 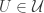 . When this is the case, the open cover
. When this is the case, the open cover  is said to be a shrinking of
is said to be a shrinking of  . If an open cover is shrinkable, we also say that the open cover can be shrunk (or has a shrinking). Whenever an open cover has a shrinking, the shrinking is indexed by the open cover that is being shrunk. Thus if the original cover is indexed in a certain way, e.g.
. If an open cover is shrinkable, we also say that the open cover can be shrunk (or has a shrinking). Whenever an open cover has a shrinking, the shrinking is indexed by the open cover that is being shrunk. Thus if the original cover is indexed in a certain way, e.g.  , then a shrinking has the same indexing, e.g.
, then a shrinking has the same indexing, e.g. 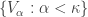 .
.
A space  is a shrinking space if every open cover of
is a shrinking space if every open cover of  is shrinkable. The property can also be broken up according to the cardinality of the open cover. Let
is shrinkable. The property can also be broken up according to the cardinality of the open cover. Let  be a cardinal. A space
be a cardinal. A space  is
is  -shrinking if every open cover of cardinality
-shrinking if every open cover of cardinality 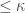 for
for  is shrinkable. A space
is shrinkable. A space  is countably shrinking if it is
is countably shrinking if it is  -shrinking.
-shrinking.
____________________________________________________________________
Examples of Shrinking
Let’s look at a few situations where open covers can be shrunk either all the time or on a limited basis. For a normal space, certain covers can be shrunk as indicated by the following theorem.
Theorem 1
The following conditions are equivalent.
- The space
 is normal.
is normal.
- Every point-finite open cover of
 is shrinkable.
is shrinkable.
- Every locally finite open cover of
 is shrinkable.
is shrinkable.
- Every finite open cover of
 is shrinkable.
is shrinkable.
- Every two-element open cover of
 is shrinkable.
is shrinkable.
The hardest direction in the proof is  , which is established in this previous post. The directions
, which is established in this previous post. The directions  are immediate. To see
are immediate. To see 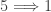 , let
, let  and
and  be two disjoint closed subsets of
be two disjoint closed subsets of  . By condition 5, the two-element open cover
. By condition 5, the two-element open cover 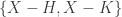 has a shrinking
has a shrinking 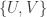 . Then
. Then  and
and 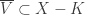 . As a result,
. As a result,  and
and  . Since the open sets
. Since the open sets  and
and  cover the whole space,
cover the whole space,  and
and  are disjoint open sets. Thus
are disjoint open sets. Thus  is normal.
is normal.
In a normal space, all finite open covers are shrinkable. In general, an infinite open cover of a normal space does not have to be shrinkable unless it is a point-finite or locally finite open cover.
The theorem of C. H. Dowker states that a normal space  is countably paracompact if and only every countable open cover of
is countably paracompact if and only every countable open cover of  is shrinkable if and only if the product space
is shrinkable if and only if the product space  is normal for every compact metric space
is normal for every compact metric space  if and only if the product space
if and only if the product space ![X \times [0,1]](https://s0.wp.com/latex.php?latex=X+%5Ctimes+%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) is normal. The theorem is discussed here. A Dowker space is a normal space that violates the theorem. Thus any Dowker space has a countably infinite open cover that cannot be shrunk, or equivalently a normal space that forms a non-normal product with a compact metric space. Thus the notion of shrinking has a connection with normality in the product spaces. A Dowker space space was constructed by M. E. Rudin in ZFC [2]. So far Rudin’s example is essentially the only ZFC Dowker space. This goes to show that finding a normal space that is not countably shrinking is not a trivial matter.
is normal. The theorem is discussed here. A Dowker space is a normal space that violates the theorem. Thus any Dowker space has a countably infinite open cover that cannot be shrunk, or equivalently a normal space that forms a non-normal product with a compact metric space. Thus the notion of shrinking has a connection with normality in the product spaces. A Dowker space space was constructed by M. E. Rudin in ZFC [2]. So far Rudin’s example is essentially the only ZFC Dowker space. This goes to show that finding a normal space that is not countably shrinking is not a trivial matter.
Several facts can be derived easily from Theorem 1 and Dowker’s theorem. For clarity, they are called out as corollaries.
Corollary 2
- All shrinking spaces are normal.
- All shrinking spaces are normal and countably paracompact.
- Any normal and metacompact space is a shrinking space.
For the first corollary, if every open cover of a space can be shrunk, then all finite open covers can be shrunk and thus the space must be normal. As indicated above, Dowker’s theorem states that in a normal space, countably paracompactness is equivalent to countably shrinking. Thus any shrinking space is normal and countably paracompact.
Though an infinite open cover of a normal space may not be shrinkable, adding an appropriate covering property to any normal space will make it into a shrinking space. An easy way is through point-finite open covers. If every open cover has a point-finite open refinement (i.e. a metacompact space), then the point-finite open refinement can be shrunk (if the space is also normal). Thus the third corollary is established. Note that the metacompact is not the best possible result. For example, it is known that any normal and submetacompact space is a shrinking space – see Theorem 6.2 of [1].
In paracompact spaces, all open covers can be shrunk. One way to see this is through Corollary 2. Any paracompact space is normal and metacompact. It is also informative to look at the following characterization of paracompact spaces.
Theorem 3
A space  is paracompact if and only if every open cover
is paracompact if and only if every open cover  of
of  has a locally finite open refinement
has a locally finite open refinement 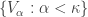 such that
such that 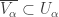 for each
for each  .
.
A proof can be found here. Thus every open cover of a paracompact space can be shrunk by a locally finite shrinking. To summarize, we have discussed the following implications.
Diagram 1
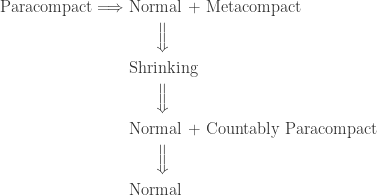
____________________________________________________________________
Three Shrinking Related Properties
None of the implications in Diagram 1 can be reversed. The last implication in the diagram cannot be reversed due to Rudin’es Dowker space. One natural example to look for would be spaces that are normal and countably paracompact but fail in shrinking at some uncountable cardinal. As indicated by the the theorem of C. H, Dowker, the notion of shrinking is intimately connected to normality in product spaces  . To further investigate, consider the following three properties.
. To further investigate, consider the following three properties.
Let  be a space. Let
be a space. Let  be an infinite cardinal. Consider the following three properties.
be an infinite cardinal. Consider the following three properties.
The space  is
is  -shrinking if and only if any open cover of cardinality
-shrinking if and only if any open cover of cardinality 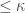 for the space
for the space  is shrinkable, i.e. the following condition holds.
is shrinkable, i.e. the following condition holds.
For each open cover  of
of  , there exists an open cover
, there exists an open cover 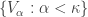 such that
such that 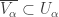 for each
for each 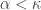 .
.
The space  has Property
has Property 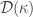 if and only if every increasing open cover of cardinality
if and only if every increasing open cover of cardinality 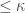 for the space
for the space  is shrinkable, i.e. the following holds.
is shrinkable, i.e. the following holds.
For each increasing open cover  of
of  , there exists an open cover
, there exists an open cover 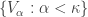 such that
such that 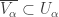 for each
for each 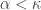 .
.
The space  has Property
has Property  if and only if the following holds.
if and only if the following holds.
For each increasing open cover  of
of  , there exists an increasing open cover
, there exists an increasing open cover 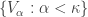 such that
such that 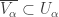 for each
for each 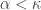 .
.
A family  is increasing if
is increasing if 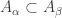 for any
for any 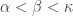 . It is decreasing if
. It is decreasing if 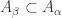 for any
for any 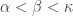 .
.
In general, any space that is  -shrinking for all cardinals
-shrinking for all cardinals  is a shrinking space as defined earlier. Any space that has property
is a shrinking space as defined earlier. Any space that has property 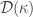 for all cardinals
for all cardinals  is said to have property
is said to have property 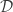 . Any space that has property
. Any space that has property  for all cardinals
for all cardinals  is said to have property
is said to have property  .
.
The first property  -shrinking is simply the shrinking property for open covers of cardinality
-shrinking is simply the shrinking property for open covers of cardinality 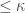 . The property
. The property 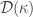 is
is  -shrinking with the additional requirement that the open covers to be shrunk must be increasing. It is clear that
-shrinking with the additional requirement that the open covers to be shrunk must be increasing. It is clear that  -shrinking implies property
-shrinking implies property 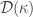 . The property
. The property  appears to be similar to
appears to be similar to 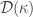 except that
except that  has the additional requirement that the shrinking is also increasing. As a result
has the additional requirement that the shrinking is also increasing. As a result  implies
implies 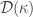 . The following diagram shows the implications.
. The following diagram shows the implications.
Diagram 2
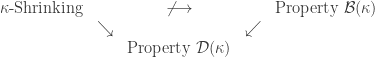
The implications in Diagram 2 are immediate. An example is given below showing that  -shrinking does not imply property
-shrinking does not imply property 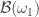 . If
. If  , then all three properties are equivalent in normal spaces, as displayed in the following diagram. The proof is in Theorem 5.
, then all three properties are equivalent in normal spaces, as displayed in the following diagram. The proof is in Theorem 5.
Diagram 3
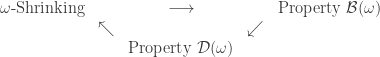
The property 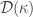 has a dual statement in terms of decreasing closed sets. The following theorem gives the dual statement.
has a dual statement in terms of decreasing closed sets. The following theorem gives the dual statement.
Theorem 4
Let  be a normal space. Let
be a normal space. Let  be an infinite cardinal. The following two properties are equivalent.
be an infinite cardinal. The following two properties are equivalent.
- The space
 has property
has property 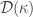 .
.
- For each decreasing family
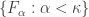 of closed subsets of
of closed subsets of  such that
such that 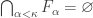 , there exists a family
, there exists a family 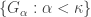 of open subsets of
of open subsets of  such that
such that  and
and 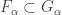 for each
for each 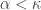 .
.
First bullet implies second bullet
Let 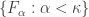 be a decreasing family of closed subsets of
be a decreasing family of closed subsets of  with empty intersection. Then
with empty intersection. Then  is an increasing family of open subsets of
is an increasing family of open subsets of  where
where  . Let
. Let 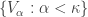 be an open cover of
be an open cover of  such that
such that 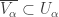 for each
for each  . Then
. Then 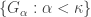 where
where 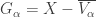 is the needed open expansion.
is the needed open expansion.
Second bullet implies first bullet
Let  be an increasing open cover of
be an increasing open cover of  . Then
. Then 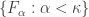 is a decreasing family of closed subsets of
is a decreasing family of closed subsets of  where
where  . Note that
. Note that 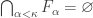 . Let
. Let 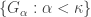 be a family of open subsets of
be a family of open subsets of  such that
such that  and
and 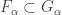 for each
for each  . For each
. For each  , there is open set
, there is open set 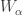 such that
such that  since
since  is normal. For each
is normal. For each  , let
, let  . Then
. Then 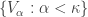 is a family of open subsets of
is a family of open subsets of  required by the first bullet. It is a cover because
required by the first bullet. It is a cover because 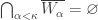 . To show
. To show 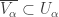 , let
, let 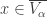 such that
such that 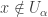 . Then
. Then  . Since
. Since 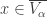 and
and 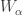 is open,
is open, 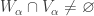 . Let
. Let 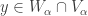 . Since
. Since  ,
, 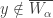 , which means
, which means  , a contradiction. Thus
, a contradiction. Thus 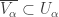 .
.
Now we show that the three properties in Diagram 3 are equivalent.
Theorem 5
Let  be a normal space. Then the following implications hold.
be a normal space. Then the following implications hold.
 -shrinking
-shrinking 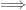 Property
Property 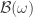
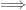 Property
Property 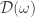
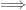
 -shrinking
-shrinking
Proof of Theorem 5
 -shrinking
-shrinking 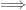 Property
Property 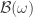
Suppose that  is
is  -shrinking. By Dowker’s theorem,
-shrinking. By Dowker’s theorem,  is a normal space. We can think of
is a normal space. We can think of 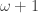 as a convergent sequence with
as a convergent sequence with  as the limit point. Let
as the limit point. Let  be an increasing open cover of
be an increasing open cover of  . Define
. Define  and
and  as follows:
as follows:
It is straightforward to verify that  and
and  are disjoint closed subsets of
are disjoint closed subsets of  . By normality, let
. By normality, let  and
and  be disjoint open subsets of
be disjoint open subsets of  such that
such that  and
and  . For each integer
. For each integer 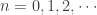 , define
, define 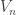 as follows:
as follows:
The set ![[n, \omega]](https://s0.wp.com/latex.php?latex=%5Bn%2C+%5Comega%5D&bg=ffffff&fg=333333&s=0&c=20201002) consists of all integers
consists of all integers  and the limit point
and the limit point  . From the way the sets
. From the way the sets 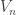 are defined,
are defined, 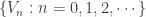 is an increasing open cover of
is an increasing open cover of  . The remaining thing to show is that
. The remaining thing to show is that 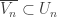 for each
for each  . Suppose that
. Suppose that  and
and  . Then
. Then 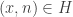 by definition of
by definition of  . There exists an open set
. There exists an open set  such that
such that  and
and 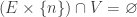 . Since
. Since  is an open set containing
is an open set containing  ,
,  . Let
. Let 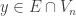 . By definition of
. By definition of 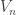 , there is some open set
, there is some open set 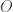 such that
such that 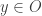 and
and ![O \times [n, \omega] \subset V](https://s0.wp.com/latex.php?latex=O+%5Ctimes+%5Bn%2C+%5Comega%5D+%5Csubset+V&bg=ffffff&fg=333333&s=0&c=20201002) , a contradiction since
, a contradiction since  is supposed to miss
is supposed to miss  . Thus
. Thus 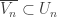 for all integers
for all integers  .
.
The direction Property 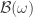
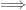 Property
Property 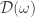 is immediate.
is immediate.
Property 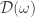
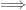
 -shrinking
-shrinking
Consider the dual condition of 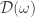 in Theorem 4, which is equivalent to
in Theorem 4, which is equivalent to  -shrinking according to Dowker’s theorem.
-shrinking according to Dowker’s theorem. 
Remarks
The direction  -shrinking
-shrinking 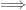 Property
Property 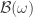 is true because
is true because  -shrinking is equivalent to the normality in the product
-shrinking is equivalent to the normality in the product  . The same is not true when
. The same is not true when  becomes an uncountable cardinal. We now show that
becomes an uncountable cardinal. We now show that  -shrinking does not imply
-shrinking does not imply  in general.
in general.
Example 1
The space  is the set of all ordinals less than
is the set of all ordinals less than  with the ordered topology. Since it is a linearly ordered space, it is a shrinking space. Thus in particular it is
with the ordered topology. Since it is a linearly ordered space, it is a shrinking space. Thus in particular it is  -shrinking. To show that
-shrinking. To show that  does not have property
does not have property 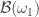 , consider the increasing open cover
, consider the increasing open cover 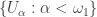 where
where 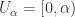 for each
for each  . Here
. Here 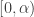 consists of all ordinals less than
consists of all ordinals less than  . Suppose
. Suppose  has property
has property 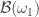 . Then let
. Then let  be an increasing open cover of
be an increasing open cover of  such that
such that 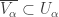 for each
for each  .
.
Let  be the set of all limit ordinals in
be the set of all limit ordinals in  . For each
. For each 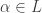 ,
, 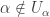 and thus
and thus  . Thus there exists a countable ordinal
. Thus there exists a countable ordinal  such that
such that ![(f(\alpha),\alpha]](https://s0.wp.com/latex.php?latex=%28f%28%5Calpha%29%2C%5Calpha%5D&bg=ffffff&fg=333333&s=0&c=20201002) misses points in
misses points in 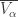 . Thus the map
. Thus the map 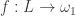 is a pressing down map. By the pressing down lemma, there exists some
is a pressing down map. By the pressing down lemma, there exists some  such that
such that 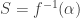 is a stationary set in
is a stationary set in  , which means that
, which means that  intersects with every closed and unbounded subset of
intersects with every closed and unbounded subset of  . This means that for each
. This means that for each 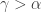 ,
, ![(\alpha, \gamma]](https://s0.wp.com/latex.php?latex=%28%5Calpha%2C+%5Cgamma%5D&bg=ffffff&fg=333333&s=0&c=20201002) would miss
would miss 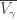 . This means that for each
. This means that for each 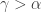 ,
, ![\overline{V_\gamma} \subset [0,\alpha]](https://s0.wp.com/latex.php?latex=%5Coverline%7BV_%5Cgamma%7D+%5Csubset+%5B0%2C%5Calpha%5D&bg=ffffff&fg=333333&s=0&c=20201002) . As a result
. As a result  would not be a cover of
would not be a cover of  , a contradiction. So
, a contradiction. So  does not have property
does not have property 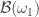 .
. 
____________________________________________________________________
Property 
Of the three properties discussed in the above section, we would like to single out property  . This property has a connection with normality in the product
. This property has a connection with normality in the product  (see Theorem 7). First, we prove a lemma that is used in proving Theorem 7.
(see Theorem 7). First, we prove a lemma that is used in proving Theorem 7.
Lemma 6
Show that the property  is hereditary with respect to closed subsets.
is hereditary with respect to closed subsets.
Proof of Lemma 6
Let  be a space with property
be a space with property  . Let
. Let  be a closed subspace of
be a closed subspace of  . Let
. Let 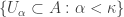 be an increasing open cover of
be an increasing open cover of  . For each
. For each  , let
, let 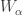 be an open subset of
be an open subset of  such that
such that  . Since the open sets
. Since the open sets 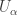 are increasing, the open sets
are increasing, the open sets 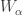 can be chosen inductively such that
can be chosen inductively such that 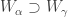 for all
for all  . This will ensure that
. This will ensure that 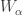 will form an increasing cover.
will form an increasing cover.
Then 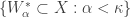 is an increasing open cover of
is an increasing open cover of  where
where 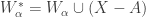 . By property
. By property  , let
, let  be an increasing open cover of
be an increasing open cover of  such that
such that 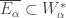 . For each
. For each  , let
, let 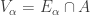 . It can be readily verified that
. It can be readily verified that 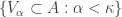 is an increasing open cover of
is an increasing open cover of  . Furthermore,
. Furthermore, 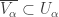 for each
for each  (closure taken in
(closure taken in  ).
). 
Let  be an infinite cardinal. Let
be an infinite cardinal. Let 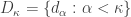 be a discrete space of cardinality
be a discrete space of cardinality  . Let
. Let  be a point not in
be a point not in  . Let
. Let 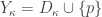 . Define a topology on
. Define a topology on 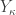 by letting
by letting  be discrete and by letting open neighborhood of
be discrete and by letting open neighborhood of  be of the form
be of the form 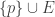 where
where 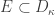 and
and 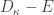 has cardinality less than
has cardinality less than  . Note the similarity between
. Note the similarity between 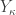 and the convergent sequence
and the convergent sequence 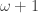 in the proof of Theorem 5.
in the proof of Theorem 5.
Theorem 7
Let  be a normal space. Then the product space
be a normal space. Then the product space 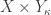 is normal if and only if
is normal if and only if  has property
has property  .
.
Remarks
The property  involves the shrinking of any increasing open cover with the added property that the shrinking is also increasing. The increasing shrinking is just what is needed to show that disjoint closed subsets of the product space can be separated.
involves the shrinking of any increasing open cover with the added property that the shrinking is also increasing. The increasing shrinking is just what is needed to show that disjoint closed subsets of the product space can be separated.
Notations
Let’s set some notations that are useful in proving Theorem 7.
- The set
![[d_\alpha,p]](https://s0.wp.com/latex.php?latex=%5Bd_%5Calpha%2Cp%5D&bg=ffffff&fg=333333&s=0&c=20201002) is an open set in
is an open set in 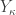 containing the point
containing the point  and is defined as follows.
and is defined as follows.
![[d_\alpha,p]=\left\{d_\beta: \alpha \le \beta<\kappa \right\} \cup \left\{p \right\}](https://s0.wp.com/latex.php?latex=%5Bd_%5Calpha%2Cp%5D%3D%5Cleft%5C%7Bd_%5Cbeta%3A+%5Calpha+%5Cle+%5Cbeta%3C%5Ckappa+%5Cright%5C%7D+%5Ccup+%5Cleft%5C%7Bp+%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
- For any two disjoint closed subsets
 and
and  of the product space
of the product space 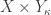 , define the following sets.
, define the following sets.
- For each
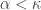 , let
, let  and
and 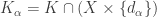 .
.
- Let
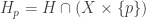 and
and 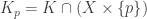 .
.
- For each
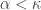 , choose open
, choose open  such that
such that 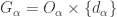 ,
, 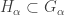 and
and 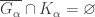 (due to normality of
(due to normality of  ).
).
- Choose open
 such that
such that 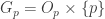 ,
,  and
and 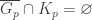 (due to normality of
(due to normality of  ).
).
Proof of Theorem 7
Suppose that  has property
has property  . Let
. Let  and
and  be two disjoint closed sets of
be two disjoint closed sets of 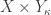 . Consider the following cases based on the locations of the closed sets
. Consider the following cases based on the locations of the closed sets  and
and  .
.
Case 1.  and
and 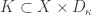 .
.
Case 2a. 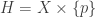
Case 2b. Exactly one of  and
and  intersect the set
intersect the set  .
.
Case 3. Both  and
and  intersect the set
intersect the set  .
.
Remarks
Case 1 is easy. Case 2a is the pivotal case. Case 2b and Case 3 use a similar idea. The result in Theorem 7 is found in [1] (Theorem 6.9 in p. 189) and [4]. The authors in these two sources claimed that Case 2a is the only case that matters, citing a lemma in another source. The lemma was not stated in these two sources and the source for the lemma is a PhD dissertation that is not readily available. Case 3 essentially uses the same idea but it has enough differences. For the sake of completeness, we work out all the cases. Case 3 applies property  twice. Despite the complicated notations, the essential idea is quite simple. If any reader finds the proof too long, just understand Case 2a and then get the gist of how the idea is applied in Case 2b and Case 3.
twice. Despite the complicated notations, the essential idea is quite simple. If any reader finds the proof too long, just understand Case 2a and then get the gist of how the idea is applied in Case 2b and Case 3.
Case 1.
 and
and 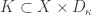 .
.
Let 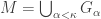 . It is clear that
. It is clear that  and
and 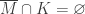 .
.
Case 2a.
Assume that 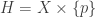 . We now proceed to separate
. We now proceed to separate  and
and  with disjoint open sets. For each
with disjoint open sets. For each 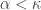 , define
, define 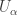 as follows:
as follows:
Then  is an increasing open cover of
is an increasing open cover of  . By property
. By property  , there is an increasing open cover
, there is an increasing open cover 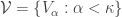 of
of  such that
such that 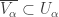 for each
for each  . The shrinking
. The shrinking  allows us to define an open set
allows us to define an open set  such that
such that 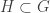 and
and 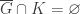 .
.
Let ![G=\cup \left\{V_\alpha \times [d_\alpha,p]: \alpha<\kappa \right\}](https://s0.wp.com/latex.php?latex=G%3D%5Ccup+%5Cleft%5C%7BV_%5Calpha+%5Ctimes+%5Bd_%5Calpha%2Cp%5D%3A+%5Calpha%3C%5Ckappa+%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) . It is clear that
. It is clear that 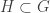 . Next, we show that
. Next, we show that 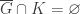 . Suppose that
. Suppose that 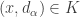 . Then
. Then ![(x,d_\alpha) \notin U_\alpha \times [d_\alpha,p]](https://s0.wp.com/latex.php?latex=%28x%2Cd_%5Calpha%29+%5Cnotin+U_%5Calpha+%5Ctimes+%5Bd_%5Calpha%2Cp%5D&bg=ffffff&fg=333333&s=0&c=20201002) . As a result,
. As a result, ![(x,d_\alpha) \notin \overline{V_\alpha} \times [d_\alpha,p]](https://s0.wp.com/latex.php?latex=%28x%2Cd_%5Calpha%29+%5Cnotin+%5Coverline%7BV_%5Calpha%7D+%5Ctimes+%5Bd_%5Calpha%2Cp%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Let
. Let 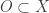 be open such that
be open such that  and
and ![(O \times \left\{d_\alpha \right\}) \cap (\overline{V_\alpha} \times [d_\alpha,p])=\varnothing](https://s0.wp.com/latex.php?latex=%28O+%5Ctimes+%5Cleft%5C%7Bd_%5Calpha+%5Cright%5C%7D%29+%5Ccap+%28%5Coverline%7BV_%5Calpha%7D+%5Ctimes+%5Bd_%5Calpha%2Cp%5D%29%3D%5Cvarnothing&bg=ffffff&fg=333333&s=0&c=20201002) . Since
. Since 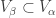 for all
for all 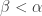 , it follows that
, it follows that ![(O \times \left\{d_\alpha \right\}) \cap (V_\beta \times [d_\beta,p])=\varnothing](https://s0.wp.com/latex.php?latex=%28O+%5Ctimes+%5Cleft%5C%7Bd_%5Calpha+%5Cright%5C%7D%29+%5Ccap+%28V_%5Cbeta+%5Ctimes+%5Bd_%5Cbeta%2Cp%5D%29%3D%5Cvarnothing&bg=ffffff&fg=333333&s=0&c=20201002) for all
for all  . It is clear that
. It is clear that ![(O \times \left\{d_\alpha \right\}) \cap (V_\gamma \times [d_\gamma,p])=\varnothing](https://s0.wp.com/latex.php?latex=%28O+%5Ctimes+%5Cleft%5C%7Bd_%5Calpha+%5Cright%5C%7D%29+%5Ccap+%28V_%5Cgamma+%5Ctimes+%5Bd_%5Cgamma%2Cp%5D%29%3D%5Cvarnothing&bg=ffffff&fg=333333&s=0&c=20201002) for all
for all 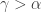 . What has been shown is that there is an open set containing the point
. What has been shown is that there is an open set containing the point 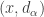 that contains no point of
that contains no point of  . This means that
. This means that 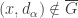 . We have established that
. We have established that 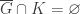 .
.
Case 2b.
Exactly one of  and
and  intersect the set
intersect the set  . We assume that
. We assume that  is the set that intersects the set
is the set that intersects the set  . The only difference between Case 2b and Case 2a is that there can be points of
. The only difference between Case 2b and Case 2a is that there can be points of  outside of
outside of  in Case 2b.
in Case 2b.
Now proceed as in Case 2a. Obtain the open cover  , the open cover
, the open cover 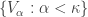 and the open set
and the open set  as in Case 2a. Let
as in Case 2a. Let  . It is clear that
. It is clear that  . We claim that
. We claim that 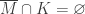 . Suppose that
. Suppose that 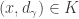 . Since
. Since 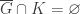 (as in Case 2a), there exists open set
(as in Case 2a), there exists open set  such that
such that 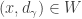 and
and 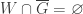 . There also exists open
. There also exists open 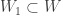 such that
such that 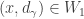 and
and  . It is clear that
. It is clear that  for all
for all 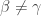 . This means that
. This means that 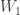 is an open set containing the point
is an open set containing the point 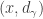 such that
such that 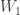 misses the open set
misses the open set  . Thus
. Thus 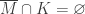 .
.
Case 3.
Both  and
and  intersect the set
intersect the set  .
.
Now project  and
and 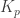 onto the space
onto the space  .
.
Note that  is simply the copy of
is simply the copy of  and
and  is the copy of
is the copy of 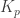 in
in  . Since
. Since  is normal, choose disjoint open sets
is normal, choose disjoint open sets  and
and  such that
such that 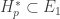 and
and 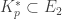 .
.
Let 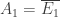 and
and 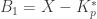 . Let
. Let 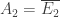 and
and 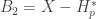 . Note that
. Note that 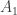 is closed in
is closed in  ,
, 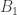 is open in
is open in  and
and  . Similarly
. Similarly 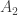 is closed in
is closed in  ,
,  is open in
is open in  and
and 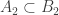 .
.
We now define two increasing open covers using property  . Define
. Define  and
and 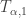 and
and 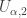 and
and 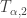 as follows:
as follows:
The open cover  is an increasing open cover of
is an increasing open cover of 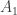 . The open cover
. The open cover  is an increasing open cover of
is an increasing open cover of 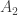 .By property
.By property  of
of 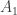 and
and 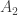 , both covers have the following as shrinking (by Lemma 6). The two shrinkings are:
, both covers have the following as shrinking (by Lemma 6). The two shrinkings are:
such that
for each 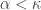 and such that both
and such that both 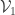 and
and 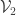 are increasing open covers. Note that the closure
are increasing open covers. Note that the closure 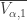 is taken in
is taken in 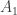 and the closure
and the closure 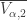 is taken in
is taken in 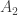 .
.
For each  , let
, let 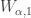 be the interior of
be the interior of 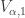 and
and 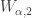 be the interior of
be the interior of 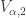 (with respect to
(with respect to  ). Note that
). Note that 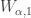 is meaningful since
is meaningful since 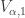 is a subset of the closure of the open set
is a subset of the closure of the open set  . Similar observation for
. Similar observation for 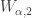 . To make the rest of the argument easier to see, note the following fact about
. To make the rest of the argument easier to see, note the following fact about 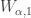 and
and 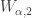 .
.
For each 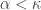 , choose open set
, choose open set  such that
such that
The last point is possible because ![U_{\alpha,2} \times [d_\alpha,p]](https://s0.wp.com/latex.php?latex=U_%7B%5Calpha%2C2%7D+%5Ctimes+%5Bd_%5Calpha%2Cp%5D&bg=ffffff&fg=333333&s=0&c=20201002) misses
misses  and
and 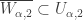 . Define the open sets
. Define the open sets  and
and  as follows:
as follows:
It is clear that  . We claim that
. We claim that 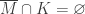 . To this end, we show that if
. To this end, we show that if 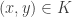 , then
, then 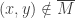 . If
. If 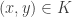 , then either
, then either 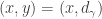 for some
for some  or
or 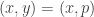 .
.
Let 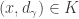 . Note that
. Note that ![(x,d_\gamma) \notin U_{\gamma,1} \times [d_\gamma,p]](https://s0.wp.com/latex.php?latex=%28x%2Cd_%5Cgamma%29+%5Cnotin+U_%7B%5Cgamma%2C1%7D+%5Ctimes+%5Bd_%5Cgamma%2Cp%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Since
. Since  ,
, ![(x,d_\gamma) \notin \overline{W_{\gamma,1}} \times [d_\gamma,p]](https://s0.wp.com/latex.php?latex=%28x%2Cd_%5Cgamma%29+%5Cnotin+%5Coverline%7BW_%7B%5Cgamma%2C1%7D%7D+%5Ctimes+%5Bd_%5Cgamma%2Cp%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Choose an open set
. Choose an open set 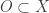 such that
such that  and
and 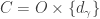 misses
misses ![\overline{W_{\gamma,1}} \times [d_\gamma,p]](https://s0.wp.com/latex.php?latex=%5Coverline%7BW_%7B%5Cgamma%2C1%7D%7D+%5Ctimes+%5Bd_%5Cgamma%2Cp%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Note that
. Note that  misses
misses ![W_{\beta,1} \times [d_\beta,p]](https://s0.wp.com/latex.php?latex=W_%7B%5Cbeta%2C1%7D+%5Ctimes+%5Bd_%5Cbeta%2Cp%5D&bg=ffffff&fg=333333&s=0&c=20201002) for all
for all 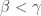 since
since  for all
for all 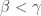 . It is clear that
. It is clear that  misses
misses ![W_{\beta,1} \times [d_\beta,p]](https://s0.wp.com/latex.php?latex=W_%7B%5Cbeta%2C1%7D+%5Ctimes+%5Bd_%5Cbeta%2Cp%5D&bg=ffffff&fg=333333&s=0&c=20201002) for all
for all  .
.
We can also choose open  such that
such that 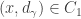 and
and  misses
misses 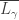 . It is clear that
. It is clear that  misses
misses 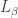 for all
for all 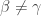 . Thus there is an open set
. Thus there is an open set  containing the point
containing the point 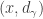 such that
such that  contains no point of
contains no point of  .
.
Let 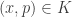 . First we find an open set
. First we find an open set  containing
containing 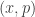 such that
such that  misses
misses  . From the way the open sets
. From the way the open sets  are defined, it follows that
are defined, it follows that ![(x,p) \notin \overline{W_{\alpha,1}} \times [d_\alpha,p]](https://s0.wp.com/latex.php?latex=%28x%2Cp%29+%5Cnotin+%5Coverline%7BW_%7B%5Calpha%2C1%7D%7D+%5Ctimes+%5Bd_%5Calpha%2Cp%5D&bg=ffffff&fg=333333&s=0&c=20201002) for all
for all  . Furthermore
. Furthermore  . Thus
. Thus  is the desired open set. On the other hand, there exists
is the desired open set. On the other hand, there exists 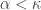 such that
such that  . Note that
. Note that 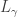 are chosen so that
are chosen so that ![(W_{\gamma,2} \times [d_\gamma,p]) \cap L_\gamma=\varnothing](https://s0.wp.com/latex.php?latex=%28W_%7B%5Cgamma%2C2%7D+%5Ctimes+%5Bd_%5Cgamma%2Cp%5D%29+%5Ccap+L_%5Cgamma%3D%5Cvarnothing&bg=ffffff&fg=333333&s=0&c=20201002) for all
for all  . Since
. Since 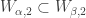 for all
for all  ,
, ![(W_{\alpha,2} \times [d_\alpha,p]) \cap L_\beta=\varnothing](https://s0.wp.com/latex.php?latex=%28W_%7B%5Calpha%2C2%7D+%5Ctimes+%5Bd_%5Calpha%2Cp%5D%29+%5Ccap+L_%5Cbeta%3D%5Cvarnothing&bg=ffffff&fg=333333&s=0&c=20201002) for all
for all  . Thus the open set
. Thus the open set ![W_{\alpha,2} \times [d_\alpha,p]](https://s0.wp.com/latex.php?latex=W_%7B%5Calpha%2C2%7D+%5Ctimes+%5Bd_%5Calpha%2Cp%5D&bg=ffffff&fg=333333&s=0&c=20201002) contains no points of
contains no points of 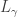 for any
for any  . Then the open set
. Then the open set ![Q \cap (W_{\alpha,2} \times [d_\alpha,p])](https://s0.wp.com/latex.php?latex=Q+%5Ccap+%28W_%7B%5Calpha%2C2%7D+%5Ctimes+%5Bd_%5Calpha%2Cp%5D%29&bg=ffffff&fg=333333&s=0&c=20201002) contains no point of
contains no point of  . This means that
. This means that 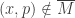 . Thus
. Thus 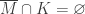 .
.
In each of the four cases (1, 2a, 2b and 3), there exists an open set 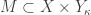 such that
such that  and
and 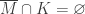 . This completes the proof that
. This completes the proof that 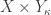 is normal assuming that
is normal assuming that  has property
has property  .
.
Now the other direction. Suppose that 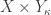 is normal. Then it can be shown that
is normal. Then it can be shown that  has property
has property  . The proof is similar to the proof for
. The proof is similar to the proof for  -shrinking
-shrinking  Property
Property  in Theorem 5.
in Theorem 5. 
____________________________________________________________________
Reference
- Morita K., Nagata J.,Topics in General Topology, Elsevier Science Publishers, B. V., The Netherlands, 1989.
- Rudin M. E., A Normal Space
 for which
for which  is not Normal, Fund. Math., 73, 179-486, 1971. (link)
is not Normal, Fund. Math., 73, 179-486, 1971. (link)
- Rudin M. E., Dowker Spaces, Handbook of Set-Theoretic Topology (K. Kunen and J. E. Vaughan, eds), Elsevier Science Publishers B. V., Amsterdam, (1984) 761-780.
- Yasui Y., On the Characterization of the
 -Property by the Normality of Product Spaces, Topology and its Applications, 15, 323-326, 1983. (abstract and paper)
-Property by the Normality of Product Spaces, Topology and its Applications, 15, 323-326, 1983. (abstract and paper)
- Yasui Y., Some Characterization of a
 -Property, TSUKUBA J. MATH., 10, No. 2, 243-247, 1986.
-Property, TSUKUBA J. MATH., 10, No. 2, 243-247, 1986.
____________________________________________________________________
where the first factor
is the space of countable ordinals with the usual order topology and the second factor
is the product of continuum many copies of the unit interval
.
is not normal, a result not shown in Steen and Seebach. The proof that was given in this site (see here) is based on an article published in 1976 [1], long before the publication date of the first edition of Steen and Seebach in 1970. It turns out that the non-normality of
was given as an exercise in Steen and Seebach in the problem section at the end of the book (problem 127 in page 211, Dover edition). Problem 127: Show that
is not normal. This indicates that the result not shown in Steen and Seebach was because it was given as a problem and not because the tool for solving it was not yet available. The fact that it is given as an exercise also means that there is a more basic proof of the non-normality of
. So, once this is realized, I set out to find a simpler proof or at least one that does not rely on the result from [1]. Interestingly, this proof brings out a broader discussion that is worthwhile and goes beyond the example at hand. The goal here is to examine the more basic proof and the broader discussion.
and its immediate successor.
is the set of all countable ordinals with the order topology. The ordinal
is the immediate successor of
. It can be regarded as the result of adding one more point to
. The extra point is
, i.e.,
with
greater than all points
. The ordinal
with the order topology is a compact space. Using interval notation,
and
. As ordinals,
is the first uncountable ordinal and
is the first uncountable successor ordinal. For more information, see here.
is a classic example of a product of a normal space (the first factor) and a compact space (the second factor) that is not normal. This example and others like it show that normality is easily broken upon taking product even if one of the factors is as nice as a compact space. The non-normality of
is discussed here. In that proof, two disjoint closed sets
and
are given such that they cannot be separated by disjoint open sets. The
and
are:
is not normal, we show that one of its closed subspaces is not normal. That closed subspace is
. To this end, we show that
can be embedded in the product space
. With a non-normal closed subspace, it follows that
is not normal. The remainder of the proof is to give the embedding.
can be embedded as a closed subspace of
, the product of
many copies of
. This means that
is also a closed subspace of
.
, define
as follows:
by letting
for all
. Consider the correspondence
with
and
. The mapping is clearly one-to-one from
onto
. Upon closer inspection, the mapping in each direction is continuous (this is a good exercise to walk through). Thus, the mapping is a homeomorphism. It follows that
can be considered a subspace of
. Since
is compact, it must be a closed subspace. With the cardinality of
being less than or equal to continuum, it follows that
can be embedded as a closed subspace of
.
, i.e., the Stone-Cech compactification of the first uncountable ordinal is its immediate successor.
, note that every continuous function defined on
is bounded and is eventually constant (see result B here). As a result, every continuous function defined on
can be extended to a continuous function defined on
. For any continuous function
, we can simply define
to be the eventual constant value. A subspace
of a space
is
-embedded in
if every bounded continuous real-valued function on
can be extended to
. According to theorem 19.12 in [4], if
is a compactification of
and if
is
-embedded in
, then
is the Stone-Cech compactification of
. Thus
is
-embedded in
and
is the Stone-Cech compactification of
. In this instance, the Stone-Cech compactification agrees with the one-point compactification. Consider the following class theorem about normality in product space. The theorem is Corollary 3.4 in the chapter on products of normal spaces in the handbook of set-theoretic topology [2].
be a space. The following conditions are equivalent.
is paracompact.
is normal.
is due to the non-normality of
. Based on this theorem, the non-normality of
is due to the non-paracompactness of
. See result G here for a proof that
is not paracompact.
is not normal. One way is the basic proof indicated above. The other way is to use Theorem 1, along with the homeomorphic embedding from
into
, the fact that
and the fact that
is not paracompact. Both are valuable. The first way is basic and is a constructive proof. Because it is more hands-on, it is a better proof to learn from. The second way provides a broader perspective that is informative but requires quoting a couple of fairly deep results. Perhaps it is best used as a second proof for perspective.
contains a copy of
, then the product space
is not normal. The contrapositive statement would be the following:
be a space. If the product space
is normal, then
cannot contain a copy of
.
, note the following about the last point:
but
for any countable
, i.e., the last point is the limit point of the set of all the points preceding it but is not in the closure of any countable set. This means that the space
does not have countable tightness (or is not countably tight). See here for definition. The property of countable tightness is hereditary. If
contains a copy of
, then
is not countably tight (or is uncountably tight). This brings us to the following theorem.
be an infinite compact space. Then
is normal if and only if
has countable tightness.
and the second factor being a compact space, the real story is the tightness of that compact space. If the tightness is countable, the product is normal. Otherwise, the product is not normal. The theorem is another reason that
is not normal. Instead of embedding
into
, we can actually show that
does not have countable tightness. This is the approach that was taken in this previous post.
), see the chapter on products of normal spaces in the handbook of set-theoretic topology [2].
2021 – Dan Ma
