Completely regular spaces (also called Tychonoff spaces) are topological spaces that come with a guarantee of having continuous real-valued functions in sufficient quantity. Thus the class of completely regular spaces is an ideal setting for many purposes that require the use of continuous real-valued functions (one example is working with function spaces). In a completely regular space , for any closed set
and for any point
not in the closed set
, there always exists a continuous function
such that
and
maps
to
. It turns out that in such a space, we can replace the point
with any compact set
that is disjoint from the closed set
. This is a useful tool for proving theorems as well as for constructing objects. In this post, we discuss and prove this result (which resembles Urysohn’s lemma) and another useful fact about completely regular spaces that works very much like Tietze’s extension theorem. Specifically we prove the following results.
-
Theorem 1
for all
,
for all
.
-
Let
-
Theorem 2
-
Let
A space is normal if any two disjoint closed sets
and
can be separated by disjoint open sets, i.e.,
and
for some disjoint open subsets
and
of
. Normal spaces are usually have the additional requirement that singleton sets are closed (i.e.
spaces).
These two theorems remind us of two important tools for normal spaces, namely Urysohn’s lemma and Tietze’s extension theorem.
Urysohn’s lemma indicates that for any two disjoint closed sets in a normal space, the space can be mapped continuously to the closed unit interval such that one closed set is mapped to
and the other closed set is mapped to
. Theorem 1 is like a weakened version of Urysohn’s lemma in that one of the two disjoint closed sets must be compact.
Tietze’s extension theorem indicates that in a normal space, any continuous real-valued function defined on a closed subspace can be extended to the entire space. Theorem 2 is like a weakened version of Tiezte’s extension theorem in that the continuous extension only works for continuous functions defined on a compact subspace.
So if one only works in a completely regular space, one can still apply these two theorems about normal spaces (the weakened versions of course). For the sake of completeness, we state these two theorems about normal spaces.
-
Urysohn’s Lemma
for all
,
for all
.
-
Let
-
Tietze’s Extension Theorem
-
Let
____________________________________________________________________
Proof of Theorem 1
We now prove Theorem 1. Let be a completely regular space. Let
and
be two disjoint closed sets where
is compact. For each
, there exists a continuous function
such that
and
. The following collection is an open cover of the compact set
.
Finitely many sets in this collection would cover since
is compact. Choose
such that
. Define
by, for each
, letting
be the minimum of
. It can be shown that the function
, being the minimum of finitely many continuous real-valued functions, is continuous. Furthermore, we have:
, and
Now define by, for each
, letting
be as follows:
It can be shown that the function is continuous. It is clear that
for all
and
for all
.
____________________________________________________________________
Proof of Theorem 2
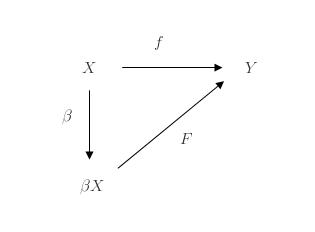
Interestingly, the proof of Theorem 2 given here uses Tietze’s extension theorem even Theorem 2 is described earlier as a weakened version of Tietze’s extension theorem. Beside using Tietze’s extension theorem, we also use the fact that any completely regular space can be embedded in a cube (see the previous post called Embedding Completely Regular Spaces into a Cube).
The proof is quite short once all the deep results that are used are understood. Let be a completely regular space. Then
can be embedded in a cube, which is a product of the closed unit interval
. Thus
is homeomorphic to a subspace of the following product space
for some index set where
for all
. We can now regard
as a subspace of the compact space
. Let
be a compact subset of
. Let
be a continuous function.
The set is a subset of
and can also be regarded as a subspace of the compact space
, which is normal. Hence Tietze’s extension theorem is applicable in
. Let
be a continuous extension of
. Let
. Then
is the required continuous extension.
____________________________________________________________________