Thinking about the Space of Irrationals Topologically

Posted on May 13, 2012 by Dan Ma

Let $\mathbb{R}$ denote the real number line and $\mathbb{P}$ denote the set of all irrational numbers. The irrational numbers and the set $\mathbb{P}$ occupy an important place in mathematics. The set $\mathbb{P}$ with the Euclidean topology inherited from the full real line is a topological space in its own right. Thus the space $\mathbb{P}$ has some of the same properties inherited from the Euclidean real line, e.g., just to name a few, it is hereditarily separable, hereditarily Lindelof, paracompact and metrizable. The space of the irrational numbers $\mathbb{P}$ has many properties apart from the full real line (e.g. $\mathbb{P}$ is totally disconnected). In this post, we look at a topological description of the space $\mathbb{P}$ .

Let $\omega$ be the set of all nonnegative integers. Then the space $\mathbb{P}$ of irrational numbers is topologically equivalent (i.e. homeomorphic to) the product space $\prod \limits_{i=0}^\infty X_i$ where each $X_i=\omega$ has the discrete topology. We will also denote the product space $\prod \limits_{i=0}^\infty X_i$ by $\omega^\omega$ . We have the following theorem.

Theorem
The space $\mathbb{P}$ of irrational numbers is homeomorphic to the product space $\omega^\omega$ .

Because of this theorem, we can look at irrational numbers as sequences of nonnegative integers. Specifically each irrational number can be identified by a unique sequence of nonnegative integers. We can think of each such unique sequence as an address to locate an irrational number. In the remainder of the post, we describe at a high level how to define the unique addresses, which will also give us a homeomorphic map between the space $\mathbb{P}$ and the product space $\omega^\omega$ .

___________________________________________________________________________

Step 0
Put the rational numbers in a sequence $r_0,r_1,r_2,r_3,\cdots$ such that $r_0=0$ . We divide the real line into countably many non-overlapping intervals. Specifically, let $A_0=[0,1]$ , $A_1=[-1,0]$ , $A_2=[1,2]$ , etc (see the following figure).

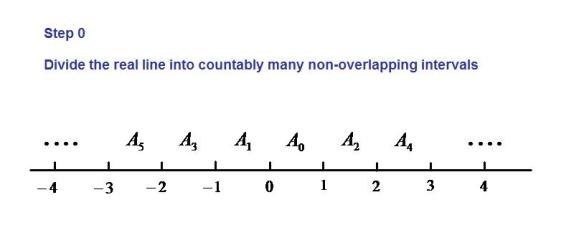
To facilitate the remaining construction, we denote the left endpoint of the interval $A_i$ by $L_i$ and denote the right endpoint by $R_i$ .

Step 1
In each of the interval $A_i$ , we further divide it into non-overlapping intervals. The left endpoint and the right endpoint of the interval $A_i$ are $L_i$ and $R_i$ , respectively. We choose a sequence $x_{i,0}, x_{i,1}, x_{i,2},\cdots$ of rational numbers converging to the right endpoint $R_i$ . Then let $A_{i,0}=[L_i,x_{i,0}]$ , $A_{i,1}=[x_{i,0},x_{i,1}]$ , $A_{i,2}=[x_{i,1},x_{i,2}]$ , etc (see the following figure).

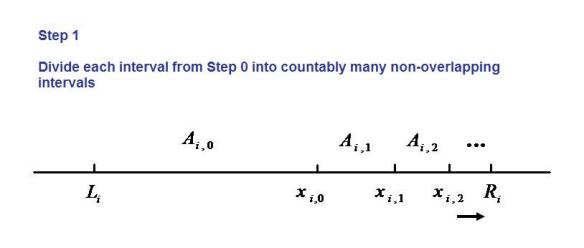
Two important points to consider in Step $1$ . One is that we make sure the rational number $r_1$ is chosen as an endpoint of some interval in Step 1. The second is that the length of each $A_{i,j}$ is less than $\displaystyle \frac{1}{2^1}$ .

Step 2
In each of the interval $A_{i,j}$ , we further divide it into non-overlapping intervals. The left endpoint and the right endpoint of the interval $A_{i,j}$ are $L_{i,j}$ and $R_{i,j}$ , respectively. We choose a sequence $x_{i,j,0}, x_{i,j,1}, x_{i,j,2},\cdots$ of rational numbers converging to the left endpoint $L_{i,j}$ . Then let $A_{i,j,0}=[x_{i,j,0},R_{i,j}]$ , $A_{i,j,1}=[x_{i,j,1},x_{i,j,0}]$ , $A_{i,j,2}=[x_{i,j,2},x_{i,j,1}]$ , etc (see the following figure).

As in the previous step, two important points to consider in Step $2$ . One is that we make sure the rational number $r_2$ is chosen as an endpoint of some interval in Step 2. The second is that the length of each $A_{i,j,k}$ is less than $\displaystyle \frac{1}{2^2}$ .

___________________________________________________________________________
Remark

In the process described above, the endpoints of the intervals $A_{f(0),\cdots,f(n)}$ are rational numbers and we make sure that all the rational numbers are used as endpoints. We also make sure that the intervals from the successive steps are nested closed intervals with lengths $\rightarrow 0$ . The consequence of this point is that the nested decreasing closed intervals will collapse to one single point (since the real line is a complete metric space) and this single point must be an irrational number (since all the rational numbers are used up as endpoints of the nested closed intervals).

In Step $i$ where $i$ is an odd integer, we make the endpoints of the new intervals converge to the right. In Step $i$ where $i>1$ is an even integer, we make the endpoints of the new intervals converge to the left. This manipulation is to ensure that the nested closed intervals will never share the same endpoint from one step all the way to the end of the process.

Thus if we have $f \in \omega^\omega$ , then $\bigcap \limits_{n=0}^\infty A_{f(0),\cdots,f(n)} \ne \varnothing$ and in fact has only one point that is an irrational number.

On the other hand, for each point $x \in \mathbb{P}$ , we can locate inductively a sequence of intervals, $A_{f(0)}, A_{f(0),f(1)}, A_{f(0),f(1),f(2)}, \cdots$ , containing the point $x$ . This sequence of nested closed intervals must collapse to a single point and the single point must be the irrational number $x$ .

The process described above gives us a one-to-one mapping from $\mathbb{P}$ onto the product space $\omega^\omega$ . This mapping is also continuous in both directions, making it a homeomorphism. the nested intervals defined above form a base for the Euclidean topology on $\mathbb{P}$ . These basic open sets have a natural correspondance with basic open sets in the product space $\omega^\omega$ .

For example, for $f \in \omega^\omega$ , $\left\{ A_{f(0),\cdots,f(n)} \cap \mathbb{P}: n \in \omega \right\}$ is a local base at the point $x \in \bigcap \limits_{n=0}^\infty A_{f(0),\cdots,f(n)}$ . One the other hand, each $A_{f(0),\cdots,f(n)} \cap \mathbb{P}$ has a natural counterpart in a basic open set in the product space, namely the following set:

$\displaystyle . \ \ \ \ \left\{g \in \omega^\omega: g \restriction n = f \restriction n \right\}$

___________________________________________________________________________

The above process establishes that the countable product of the integers, $\omega^\omega$ , is equivalent topologically to the Euclidean space $\mathbb{P}$ .

An elementary example of a productively Lindelof space

Posted on May 2, 2011 by Dan Ma

A topological space is productively Lindelof if its product with every Lindelof space is Lindelof. It is well known that the product of a compact space with any Lindelof space is Lindelof. As a corollary, the product of a $\sigma$ -compact space with any Lindelof space is Lindelof. Another way to state this basic topological fact is that $\sigma$ -compact spaces are productively Lindelof. We present an example of a productively Lindelof space that is not $\sigma$ -compact, demonstrating that these two notions are not equivalent. This example is an elementary one. No heavy machinery is required to define the example. References for productively Lindelof spaces include [1] and [3].

The fact that the product of any $\sigma$ -compact space with any Lindelof space is Lindelof is due to the Tube Lemma.

We now define a productively Lindelof space that is not $\sigma$ -compact. Let $X= \left\{p\right\} \cup D$ where $D$ is any uncountable set and $p \notin D$ . The set $D$ is discrete in $X$ and open neighborhoods at $p$ have the form $\left\{p\right\} \cup (D-A)$ where $A \subset D$ is countable. The only compact subsets of this space are finite sets. Thus $X$ is not $\sigma$ -compact.

To see that $X$ is productively Lindelof, let $Y$ be any Lindelof space. Let $\mathcal{U}$ be any open cover of $X \times Y$ . Assume that $\mathcal{U}$ consists of open sets of the form $G \times H$ where $G$ is open in $X$ and $H$ is open in $Y$ .

There exists a countable $\mathcal{V} \subset \mathcal{U}$ such that $\mathcal{V}$ covers $\left\{p\right\} \times Y$ . Suppose that $\mathcal{V}=\left\{G_1 \times H_1,G_2 \times H_2,G_3 \times H_3,\cdots \right\}$ . Also assume that for each $i$ , $G_i=\left\{p\right\} \cup (D-A_i)$ where $A_i$ is countable.

Note that each $A_i \times Y$ is a Lindelof space since it is the product of a countable space (thus $\sigma$ -compact) with a Lindelof space. It is also clear that each point $(x,y) \in X \times Y$ either belongs to a set in $\mathcal{V}$ or to $A_i \times Y$ for some $i$ .

For each $i$ , choose countable $\mathcal{W}_i \subset \mathcal{U}$ such that $\mathcal{W}_i$ covers $A_i \times Y$ . Then $\mathcal{V} \cup \mathcal{W}_1 \cup \mathcal{W}_2 \cup \cdots$ is a countable subcover of $\mathcal{U}$ .

Reference

Alster, K., On spaces whose product with every Lindelof space is Lindelof, Colloq. Math. 54 (1987), 171–178.
Engelking, R., General Topology, Revised and Completed edition, 1989, Heldermann Verlag, Berlin.
Tall, F., Productively Lindelof spaces may all be D, Canad. Math. Bull. to apear.
Willard, S., General Topology, 1970, Addison-Wesley Publishing Company.

An observation about hereditarily separable function spaces

Posted on April 9, 2011 by Dan Ma

For any completely regular space $X$ , by $C_p(X)$ we mean the space of all real-valued continuous functions on $X$ endowed with the pointwise convergent topology. It is known that $C_p(X)$ is hereditarily separable if and only if $X^n$ is hereditarily Lindelof for all positive integer $n$ if and only if $X^\omega$ is hereditarily Lindelof where $\omega$ is the first infinite ordinal (a result that follows from a theorem of Zenor in [4]). This result points to a duality between hereditary separability of the function space $C_p(X)$ and the hereditary Lindelof property of the domain space $X$ and is restated below.

Theorem
Let $X$ be a completely regular space. Then the following conditions are equivalent:

$C_p(X)$ is hereditarily separable.
$X^n$ is hereditarily Lindelof for all positive integer $n$ .
$X^\omega$ is hereditarily Lindelof.

As an introduction to this theorem, we present the proof to one direction of this theorem for $n=1$ .

Observation
Let $X$ be any completely regular space. We have the following obervation:

If $C_p(X)$ is hereditarily separable, then $X$ is hereditarily Lindelof.

Suppose $X$ is not hereditarily Lindelof. We aim to show that $C_p(X)$ is not hereditarily separable by producing a non-separable subspace $\mathcal{F}$ of $C_p(X)$ .

Let $Y \subset X$ be a subspace that is not Lindelof. Let $\mathcal{U}$ be a collection of open subsets of $X$ such that $\mathcal{U}$ covers $Y$ and no countable subcollection of $\mathcal{U}$ covers $Y$ .

For each $y \in Y$ , choose $U_y \in \mathcal{U}$ such that $y \in U_y$ . By the completely regularity of $X$ , choose a continuous $f_y: X \rightarrow \mathbb{R}$ such that $f_y$ maps $X-U_y$ to $0$ and $f_y(y)=1$ . Let $\mathcal{F}=\left\{f_y:y \in X \right\}$ . It can be shown that $\mathcal{F}$ is a non-separable subspace of $C_p(X)$ . That is, no countable subset of $\mathcal{F}$ can be dense in $\mathcal{F}$ . $\blacksquare$

For any completely regular space $X$ , it is also known (see [2]) that $C_p(X)$ is separable if and only if $X$ has a weaker separable metrizable topology (i.e. $X$ has a weaker topology such that $X$ with this weaker topology is a separable metrizable space). The result in [2] combined with the observation presented here provides a way to obtain sepearable $C_p(X)$ that is not hereditarily separable. Look for any $X$ that is not hereditarily Lindelof but has a weaker separable metrizable topology. One such example is the Michael Line.

The observation we make here is a rather weak result. The double arrow space $Z$ is hereditarily Lindelof. Yet $C_p(Z)$ is not even separable since $Z$ is compact space that is not metrizable. Note that $Z^2$ is not hereditarily Lindelof since it contains a copy of the Sorgenfrey plane (see the previous post on double arrow space).

Reference

Engelking, R., General Topology, Revised and Completed edition, 1989, Heldermann Verlag, Berlin.
Noble, N., The density character of function spaces, Proc. Amer. Math. Soc. 42:1 (1974) 228-233.
Willard, S., General Topology, 1970, Addison-Wesley Publishing Company.
Zenor, P., Hereditarily m-separability and the hereditarily m-lindelof property in product spaces and function spaces, Fund. Math. 106 (1980), 175-180

Closed uncountable subsets of the real line

Posted on June 3, 2010 by Dan Ma

This is post #12 of the series on the Euclidean topology of the real line. See the links at the bottom for other posts in the series.

In the previous post Perfect sets and Cantor sets, II, we show that every subset of the real line that is a perfect set contains a Cantor set and thus has cardinality continuum. We would like to add an observation that every uncountable closed subset of the real line contains a perfect set. Thus every uncountable closed subset of the real line contains a Cantor set and thus has the same cardinality as the real line itself.

Recall that a subset $A$ of the real line is a perfect set if it is closed and every point of $A$ is a limit point of $A$ . In the previous post Perfect sets and Cantor sets, II, we demonstrate a procedure for constructing a Cantor set out of any nonempty perfect set. In another post The Lindelof property of the real line, we show that every uncountable subset $A$ of the real line contains at least one of its limit points. Thus all but countably many points of $A$ are limit points of $A$ . Consequently, for any uncountable closed subset $A$ of the real line, all but countably many points of $A$ are limit points of $A$ . By removing the countably many non-limit points (isolated points), we have a perfect set.

Links to previous posts on the topology of the real line:
1. The Euclidean topology of the real line (1)
2. The Euclidean topology of the real line (2)
3. The Euclidean topology of the real line (3) – Completeness
4. The Euclidean topology of the real line (4) – Compactness
5. The Cantor bus tour
6. The Cantor set, I
7. The Cantor set, II
8. The Cantor set, III
9. Perfect sets and Cantor sets, I
10. The Lindelof property of the real line
11. Perfect sets and Cantor sets, II

Perfect sets and Cantor sets, II

Posted on May 30, 2010 by Dan Ma

This is post #11 of the series on the Euclidean topology of the real line. See the links at the bottom for other posts in the series.

In the previous post Perfect sets and Cantor sets, I, we show that every nonempty perfect set is uncountable. We now show that any perfect contains a Cantor set. Hence the cardinality of any perfect set is continuum.

Given a perfect set $W$ , we construct a Cantor set within $W$ . Consider the following cases:

Case 1. $W$ contains some bounded closed interval $[a,b]$ .
Case 2. $W$ does not any bounded closed interval.

If case 1 holds, then we can apply the middle third process on $[a,b]$ and produce a Cantor set. So in the remaining dicussion of this post, we assume case 2 holds. This means that for each closed interval $[a,b]$ , there is some $x \in [a,b]$ such that $x \notin W$ .

Background Discussion
Let $A \subset \mathbb{R}$ and $p \in A$ . The point $p$ is a right-sided limit point of $A$ if for each open interval $(a,b)$ containing $p$ , the open interval $(p,b)$ contains a point of $A$ . The point $p$ is a left-sided limit point of $A$ if for each open interval $(a,b)$ containing $p$ , the open interval $(a,p)$ contains a point of $A$ . The point $p$ is a two-sided limit point of $A$ if it is both a right-sided limit point and a left-sided limit point of $A$ . For the proof of the following lemma, see the post labeled #10 listed below.

In Lemma 2 below, we apply the least upper bound property and the greatest lower bound property. See the post labeled #4 listed below.

Key Lemmas for Construction

Lemma 1
Suppose that $X \subset \mathbb{R}$ is an uncountable set. Then $X$ contains a two-sided limit point.

As a corollary to the lemma 1, for the perfect set $W$ in question, all but countably many points of $W$ are two-sided limit points of $W$ .

Lemma 2
Suppose $E \subset \mathbb{R}$ is a nonempty perfect set that satisfies Case 2 indicated above. Suppose that for the closed interval $[a,b]$ , we have:

$(a,b) \cap E \ne \phi$ ,
the left endpoint $a$ is a right-sided limit point of $E$ ,
the right endpoint $b$ is a left-sided limit point of $E$ .

Then we have $a<a^*<b^*<b$ such that:

there are no points of $E$ in the open interval $(a^*,b^*)$ ,
the point $a^*$ is a left-sided limit point of $E$ ,
the point $b^*$ is a right-sided limit point of $E$ .

Proof. Since Case 2 holds, for the closed interval $[a,b]$ in question, there is some $x \in (a,b)$ such that $x \notin E$ . Then we can find an open interval $(c,d)$ such that $x \in (c,d)$ and $a<c<d<b$ and $(c,d) \cap E = \phi$ .

Any point in $(c,d)$ is an upper bound of $W_1=[a,c) \cap E$ . By the least upper bound property, $W_1$ has a least upper bound $a^*$ . Any point in $(c,d)$ is an lower bound of $W_2=(d,b] \cap E$ . By the greatest lower bound property, $W_2$ has a greatest lower bound $b^*$ . Then $a^*$ and $b^*$ satisfy the conclusion of the lemma. $\blacksquare$

Lemma 3
Suppose $E \subset \mathbb{R}$ is a nonempty perfect set. Suppose we have a closed interval $[s,t]$ such that the left endpoint $s$ is a right-sided limit point of $E$ and the right endpoint $t$ is a left-sided limit points of $E$ . Then we have $s<s_*<t_*<t$ such that:

the open interval $(s_*,t_*)$ contains points of $E$ ,
both endpoints $s_*$ and $t_*$ are two-sided limit points of $E$ ,
$t_*-s_*<0.5(t-s)$ .

Proof. Suppose we have a closed interval $[s,t]$ as described in the lemma. Then $E_1=[s,t] \cap E$ is a nonempty perfect set. Thus $E_1$ is uncountable. So pick $p \in (s,t)$ such that $p$ is a two-sided limit point of $E_1$ .

Choose open interval $(c,d)$ such that $s<c<p<d<t$ and $d-c<0.5(t-s)$ . Since $p$ is a two-sided limit point of $E_1$ , choose $s^*$ and $t^*$ such that $c<s^*<p$ , $p<t^*<d$ and both $s^*$ and $t^*$ are two-sided limit points of $E_1$ . It follows that $s^*$ and $t^*$ satisfy the conclusion of the lemma. $\blacksquare$

Lemma 4
Suppose $E \subset \mathbb{R}$ is a nonempty perfect set that satisfies Case 2 indicated above. Suppose we have a closed interval $[a,b]$ such that the endpoints are two-sided limit points of $E$ . Then we have disjoint closed intervals $K_0=[p_0,q_0]$ and $K_1=[p_1,q_1]$ such that

$K_0 \subset [a,b]$ and $K_1 \subset [a,b]$ ,
the lengths of both $K_0$ and $K_1$ are less then $0.5(b-a)$ ,
for each of $K_0$ and $K_1$ , the endpoints are two-sided limit points of $E$ .

Proof. This is the crux of the construction of a Cantor set from a perfect set and is the result of applying Lemma 2 and Lemma 3.

Applying Lemma 2 on $[a,b]$ and obtain the open interval $(a^*,b^*)$ . We remove the open interval $(a^*,b^*)$ from $[a,b]$ and obtain two disjoint closed intervals $[a,a^*]$ and $[b^*,b]$ . Each of these two subintervals contains points of the perfect set $W$ since the endpoints are limit points of $W$ in the correct direction.

Now apply Lemm 3 to shrink $[a,a^*]$ to obtain a smaller subinterval $K_0=[p_0,q_0]$ such that the length of $K_0$ is less than $0.5(a^*-a)$ and is thus less than $0.5(b-a)$ . Likewise, apply Lemma 3 on $[b^*,b]$ to obtain $K_1=[p_1,q_1]$ such that the length of $K_1$ is less than $0.5(b-b^*)$ and is thus less than $0.5(b-a)$ . Note that both $K_0$ and $K_1$ constain points of $E$ , making both $K_0 \cap E$ and $K_1 \cap E$ perfect sets and compact sets. $\blacksquare$

Construction
Suppose $W \subset \mathbb{R}$ is a nonempty perfect set that satisfies Case 2. Pick two two-sided limit $a_0$ and $b_0$ of $W$ . Obtain $B_0=K_0$ and $B_1=K_1$ as a result of applying Lemma 4. Let $A_1=B_0 \cup B_1$ .

Then we apply Lemma 4 on the closed interval $B_0$ and obtain closed intervals $B_{00}$ , $B_{01}$ . Likewise we apply Lemma 4 on the closed interval $B_1$ and obtain closed intervals $B_{10}$ , $B_{11}$ . Let $A_2=B_{00} \cup B_{01} \cup B_{10} \cup B_{11}$ .

Continue this induction process. Let $C=\bigcap \limits_{n=1}^{\infty} A_n$ . The set $C$ is a Cantor set and has all the properties discussed in the posts labled #6 and #7 lised at the end of this post.

We claim that $C \subset W$ . For any countably infinite sequence $g$ of zeros and ones, let $g_n$ be the first $n$ terms in $g$ . Let $y \in C$ . Then $\left\{y\right\}=\bigcap \limits_{n=1}^{\infty} B_{g_n}$ for some countably infinite sequence $g$ of zeros and ones (see post #6 listed below). Then every open interval $(a,b)$ containing $y$ would contain some closed interval $B_{g_n}$ . Thus $y$ is a limit point of $W$ . Hence $y \in W$ .

The Lindelof property of the real line

Posted on May 29, 2010 by Dan Ma

This is post #10 of the series on the Euclidean topology of the real line. See the links at the bottom for other posts in the series.

In the real line, the set $\mathbb{Z}$ of all integers (positive, negative and zero) is a closed set as well as a discrete set. It is closed because the complement is an open set. It is discrete since no point of $\mathbb{Z}$ is a limit point of $\mathbb{Z}$ . It turns out that in the real line, only countable sets can be both closed and discrete. Equivalently, the real line satisfies the following property:

$* \$ Every uncountable subset has a limit point.

A set $A \subset \mathbb{R}$ is discrete if no point of $A$ is a limit point of $A$ . The set $H=\left\{\frac{1}{n}: n=1,2,3,\cdots\right\}$ is a discrete set, as is the set $\mathbb{Z}$ . However, unlike $\mathbb{Z}$ , the set $H$ is not a closed set. It turns out that in the real line, only countable sets can be discrete. Equivalently, the real line satisfies the following property:

$** \$ Every uncountable subset contains one of its limit points.

It follows that for any uncountable subset $A$ of the real line, all but countably many points of $A$ are limit points of $A$ .

We show that both the statements $*$ and $**$ are intimately tied to the Lindelof property. Specifically, both $*$ and $**$ hold for the real line because the real line itself and every subset of the real line has the Lindelof property.

We also prove that for every uncountable subset $A$ of the real line, there is at least one $p \in A$ such that $p$ is a two-side limit point of $A$ . It follows that for every uncountable subset $A$ of the real line, all but countably many points of $A$ are two-sided limit points of $A$ .

Definitions
Let $X$ be a topological space. A collection $\mathcal{U}$ of subsets of $X$ is said to be a cover of $X$ if every point of $X$ belongs to some set in $\mathcal{U}$ . The collection $\mathcal{U}$ is said to be an open cover if it is a cover of $X$ and it consists entirely of open subsets of $X$ . If $\mathcal{U}$ is an open cover of $X$ and if $\mathcal{V} \subset \mathcal{U}$ also covers $X$ , then $\mathcal{V}$ is said to be a subcover of $\mathcal{U}$ .

The space $X$ is said to be a Lindelof space (or has the Lindelof property) if every open cover of $X$ has a countable subcover. The space $X$ is said to be hereditarily Lindelof if every subspace of $X$ is a Lindelof space.

Theorem 1
Let $X$ be a topological space.

If $X$ is Lindelof, then $X$ satisfies the property $*$ .
If $X$ is hereditarily Lindelof, then $X$ satisfies the property $**$ .

Proof. We prove the contrapositive, that is, if $X$ has an uncountable subset that has no limit point, then $X$ is not Lindelof. Let $A \subset X$ be uncountable such that $A$ has no limit point. Then $A$ is a closed set. For each $x \in A$ , there is an open set $O_x$ such that $x \in O_x$ and $O_x$ contains no point of $A$ other than $x$ . Then the following is an open cover of $X$ :

$\mathcal{U}=\displaystyle \left\{O_x: x \in A\right\} \cup \left\{X-A\right\}$

Note that only countably many $O_x$ cannot cover $A$ . Thus $\mathcal{U}$ is an open cover of $X$ that has no countable subcover, showing that $X$ is not Lindelof.

To show 2, we also prove the contrapositive. Let $A \subset X$ be some uncountable set such that no point of $A$ is a limit point of $A$ . Then for each $x \in A$ , $\left\{x\right\}$ is an open set relative to $A$ . Thus the subspace $A$ is not Lindelof, showing that $X$ is not hereditarily Lindelof. $\blacksquare$

Theorem 2
Every subset of the real line $\mathbb{R}$ has the Lindelof property, i.e. $\mathbb{R}$ is hereditarily Lindelof.

Remark. This follows from Lemma 4 in the post labeled #4 listed below. This theorem follows from the fact that the Euclidean topology of the real line is generated by a countable base (specifically, the open intervals with rational numbers as endpoints).

Corollary 3
The real line satisfies properties $*$ and $**$ . Thus we have:

Every uncountable subset of the real line has a limit point.
Every uncountable subset of the real line contains one of its limit points.

Remark
This follows from Theorem 1 and Theorem 2. It also follows that if $A$ is an uncountable subset of the real line, all but countably many points of $A$ are limit points of $A$ . $\blacksquare$

Let $A \subset \mathbb{R}$ and $p \in A$ . The point $p$ is said to be right-sided limit point of $A$ if for each open interval $(a,b)$ such that $p \in (a,b)$ , we have $(p,b) \cap A \ne \phi$ . The point $p$ is said to be left-sided limit point of $A$ if for each open interval $(a,b)$ such that $p \in (a,b)$ , we have $(a,p) \cap A \ne \phi$ . The point $p$ is said to be a two-sided limit point of $A$ if it is both a right-sided and left-sided limit point.

Based on the discussion in the previous post on completness (the post labeled #3 below), we can assume the least upper property whenever we work with the real line. This property states that for every subset $A$ of the real line, if $A$ is bounded above, then $A$ has a least upper bound (the upper bound that is the smallest among all the upper bounds). This assumption simplies the proof of the next theorem. The least upper bound property is equivalent to the greatest lower bound property, which states that for every subset $A$ of the real line, if $A$ is bounded below, then $A$ has a greatest lower bound (the lower bound that is the greatest among all the lower bounds).

Theorem 4
Every uncountable subset of the real line has at least one point that is a two-sided limit point.

Proof. Suppose that $A \subset \mathbb{R}$ is an uncountable set such that none of its points is a two-sided limit point. By corollary 3, all but countably many points of $A$ is a limit point of $A$ . So by removing these countably many points if necessary, assume that every point of $A$ is a limit point of $A$ .

For each $x \in A$ , $x$ is either a right-sided limit point of $A$ or a left-sided limit point of $A$ but not both. So either $(1)$ there are uncountably many points of $A$ that are left-sided limit points of $A$ or $(2)$ there are uncountably many points of $A$ that are right-sided limit points of $A$ . Assume $(1)$ and use the least upper bound property. The proof assuming $(2)$ is similar and uses the greatest lower bound property.

Let $B$ be the set of all points of $A$ that are left-sided limit points of $A$ . By assumption $(1)$ , $B$ is uncountable. For each $x \in B$ , choose a rational number $b_x$ such that $(x,b_x)$ contains no point of $A$ . Then there must be some rational number $r$ such that $r=b_x$ for uncountably many $x \in B$ . Thus the following set $C$ is uncountable:

$\displaystyle C=\left\{x \in B: b_x=r\right\}$

Note that the rational number $r$ is an upper bound of $C$ . By the least upper bound property, let $u$ be the least upper bound of $C$ . Choose some $y \in C$ such that $y<u$ . This is possible since $x \le u$ for all $x \in C$ and $C$ is uncountable. There must be some $z \in C$ such that $y<z<u$ . Otherwise, $y$ would be an upper bound. Since $z$ is a left-sided limit point of $A$ , $(y,z)$ contains infinitely many points of $A$ . But $(y, b_y)=(y,r)$ is supposed to contain no points of $A$ , a contradiction.

Under assumption $(2)$ , the proof is similar and uses the greatest lower bound property. Thus we establish that in each uncountable subset of the real line, one of its points must be a two-sided limit point. As a corollary to this fact, all but countably many points of an uncountable set of real numbers must be two-sided limit points of the set. $\blacksquare$

Perfect sets and Cantor sets, I

Posted on May 27, 2010 by Dan Ma

This is post #9 of the series on the Euclidean topology of the real line. See the links at the bottom for other posts in the series.

Recall that a subset $A$ of the real line is a perfect set if $A$ is closed in Euclidean topology of the real line and that every point of $A$ is a limit point of $A$ . Any closed and bounded interval $[a,b]$ is a perfect set. The Cantor sets (the middle third version and other variations) are perfect sets (see the links #7 and #8 below). It turns out that any nonempty perfect set contains a Cantor set. In this series of posts on Euclidean topology of the real line, by Cantor sets we mean any set that can be constructed by a binary process of splitting closed intervals into two halves at each stage (see links for #6 and #8 below). We demonstrate the algorithm of constructing a Cantor set from any perfect set. This post (part I) shows that any nonempty perfect set is uncountable. Knowing that a perfect is uncountable will simplify the construction process (next post).

Suppose $W \subset \mathbb{R}$ is a nonempty perfect subset. We show that $W$ is uncountable. Since $W$ has at least one point and every point is a limit point, $W$ is infinite. The key to showing $W$ is uncountable is that every nested decreasing sequence of compact subsets of the real line (actually in any topological space) has nonempty intersection. If $W$ happens to be countable, we can define a nested sequence of compact subsets of $W$ with empty intersection. Thus $W$ cannot be countable.

The following lemma is a corollary to Theorem 3 in the post # 4 listed below. The lemma applies to any abstract spaces where compactness can be defined. We state the lemma in terms of the real line since this is our focus.

Lemma
Suppose $C_1,C_2,C_3, \cdots$ are compact subsets of the real line such that

$\displaystyle C_1 \supset C_2 \supset C_3 \supset \cdots$ .

Then $\bigcap \limits_{n=1}^{\infty} C_n \ne \phi$ .

To make the argument that $W$ is uncountable more precise, suppose that $W$ is countable. Then we can enumerate $W$ in a sequence indexed by the positive integers. We have:

$\displaystyle W=\left\{w_1,w_2,w_3,\cdots\right\}$

Pick a bounded open interval $O_1$ such that $w_1 \in O_1$ . Next, pick an open interval $O_2$ such that $\overline{O_2} \subset O_1$ and $w_2 \notin \overline{O_2}$ and $O_2 \cap W \ne \phi$ .

In the $n^{th}$ stage where $n \ge 2$ , pick an open interval $O_n$ such that $\overline{O_n} \subset O_{n-1}$ and $w_n \notin \overline{O_n}$ and $O_n \cap W \ne \phi$ . Since $W$ is a perfect set, the induction step can continue at every stage.

Now, let $C_n=\overline{O_n} \cap W$ . Note that $C_n$ is a compact set since $\overline{O_n}$ is compact. By the lemma, the intersection of the $C_n$ must be nonempty. By the induction steps, no point of $W$ belongs to all the sets $\overline{O_n}$ , implying the intersection of $C_n$ is empty, a contradiction. Thus $W$ must be uncountable.

Remark
As a corollary, the real line and the unit intervals are uncountable. A more interesting corollary is that any nonempty perfect set has a two-sided limit point. In fact all but countably many points of a nonempty perfect set are two sided limit points. See the post The Lindelof property of the real line for a proof that any uncountable subset of the real line has a two sided limit point. This fact will simplify the construction of a Cantor set from a perfect set.

Reference

Rudin, W., Principles of Mathematical Analysis, Third Edition, 1976, McGraw-Hill, Inc, New York.

The Cantor set, III

Posted on May 23, 2010 by Dan Ma

This is post # 8 of the series on the Euclidean topology of the real line. See the links at the bottom for other posts in the series.

The Cantor set, I
The Cantor set, II

In two previous posts (see links above), we discuss the “middle third” Cantor set constructed on the unit interval. In this post, we discuss two variations on this construction. In the first variation, the lengths of the removed intervals sum to 1 (hence these Cantor sets have zero Lebesgue measure). The middle third construction is a specific example if this algorithm. In the second variation, the sum of the lengths of removed intervals is less than one. Thus these Cantor sets have positive Lebesgue measure. However, the resulting Cantor sets from either approach have the same topological properties.

The Middle k Cantor Set
Let $0<k<1$ . In this construction, we remove the middle $k^{th}$ open interval of $[0,1]$ . This removed open interval has length $k$ and the remaining set has length $1-k$ .

In the second stage, for each of the two remaining two closed intervals, we remove the middle $k^{th}$ open interval. The two removed open intervals have a combined length of $(1-k)k$ . Thus, the length of the remaining set is $(1-k)-(1-k)k=(1-k)^2$ .

In the third stage, the four removed intervals have a combined length of $(1-k)^2k$ . Then the remaining set has length:

$(1-k)^2-(1-k)^2k=(1-k)^3$ .

When the inductive process is completed, the set of the remaining points is a Cantor set. The total length of removed open intervals is:

$\displaystyle k+(1-k)k+(1-k)^2k+ \cdots=1$

When $k=\frac{1}{3}$ , we have the middle third Cantor set that is constructed in the previous post The Cantor set, I. Whether $k=\frac{1}{3}$ or another fraction, the resulting Cantor sets have the same properties. This middle $k$ process always produces a compact subset of the real line that has cardinality continuum, which is also a perfect set and a nowhere dense set in $[0,1]$ as well as a totally disconnected set. In other words, all the properties discussed in the two previous posts (see the links indicated above) hold for the Cantor sets produced by this middle $k$ algorithm.

The Cantor Sets of Positive Measure
Pick a sequence $\left\{a_n\right\}$ such that $0<\sum \limits_{n=1}^{\infty} a_n<1$ . For the illustration here, we use $a_n=\frac{1}{2^{n+1}}$ where $n=1,2,3,\cdots$ . Note that $\sum \limits_{n=1}^{\infty} a_n=\frac{1}{2}$ .

In this construction, we still remove the middle open interval in any remaining closed interval. The key is that in each stage we remove open intervals with a total length of $a_n=\frac{1}{2^{n+1}}$ . In the end, the removed intervals have a total length of $\frac{1}{2}$ , making the left over piece of length $\frac{1}{2}$ .

In stage $n=1$ , we remove the middle $\frac{1}{2^2}$ open interval of $[0,1]$ . In stage $n=2$ , in each of the remaining two closed intervals, we remove the middle part such that the two removed open intervals have equal length and the combined length of $\frac{1}{2^3}$ .

In stage $n=3$ , the four removed open intervals are of equal length and with a combined total length of $\frac{1}{2^4}$ .

Continue with the inductive process, making sure that any removed open interval is the middle part of the remaining closed interval. When it is done, the removed open intervals have a total length of $\frac{1}{2}$ . The set of the remaining points is a Cantor set of length $\frac{1}{2}$ . Other than having positive Lebesgue measure, the Cantor sets produced by this algorithm have the same topological properties as the middle third Cantor set, namely, being totally disconnected and a perfect set.

Links to previous posts on the topology of the real line:
The Euclidean topology of the real line (1)
The Euclidean topology of the real line (2)
The Euclidean topology of the real line (3) – Completeness
The Euclidean topology of the real line (4) – Compactness
The Cantor bus tour
The Cantor set, I
The Cantor set, II

The Cantor set, II

Posted on May 23, 2010 by Dan Ma

This is post # 7 of the series on the Euclidean topology of the real line. See the links at the bottom for other posts in the series.

In the previous post The Cantor set, I, we constructed the “middle third” Cantor set and we showed that it has cardinality continuum. In this post we discuss some basic topological properties of the Cantor set.

The Cantor set we defined in the previous post is the “middle third” Cantor set, the traditional version found in many texts. In this “middle third” recipe, the open interval in the middle third of $[0,1]$ is taken out. Two closed intervals remain. In each of the succeeding stages, the open interval in the middle third of any remaining closed interval is removed. After the inductive process is completed, the remaining points form the Cantor set. Note that the open intervals removed in this process have a total length of $1$ since $\frac{1}{3}+\frac{2}{3^2}+\frac{2^2}{3^3}+\cdots =1$ . Yet the points remained have the same cardinality as the unit interval $[0,1]$ .

There are other striking properties about the Cantor set. For example, the Cantor set contains no open intervals $(a,b)$ . This makes the Cantor set a very “thin” set (a nowhere dense set). On the other hand, the Cantor set has no isolated points since every point of the Cantor set is a limit point of itself.

Cantor Set Preliminary
Let $C$ be the Cantor set as defined in the previous post. Recall that $C=\bigcap \limits_{n=0}^{\infty}A_n$ where

$A_0=[0,1]$
$A_1=B_0 \cup B_1$
$A_2=B_{00} \cup B_{01} \cup B_{10} \cup B_{11}$
$A_3=B_{000} \cup B_{001} \cup B_{010} \cup B_{011} \cup B_{100} \cup B_{101} \cup B_{110} \cup B_{111}$
and so on.

Each $B_g$ , where $g$ is a string of zeros and ones of finite length, is a closed interval and is obtained by removing the middle third of the previous closed interval. For example, $B_{010}$ and $B_{011}$ are obtained by removing the middle third of the closed interval $B_{01}$ . Refer to the previous post The Cantor set, I for more information about the construction.

Each point $y \in C$ is the single point in the intersection of a nested decreasing sequence of $B_g$ , i,e, $\left\{y\right\}=\bigcap \limits_{n=1}^{\infty}B_{g_n}$ where $g_i$ and $g_j$ agree on the first $i$ many coordinates if $i<j$ . The $g_n$ can be obtained by tracing the construction steps. For example, $y \in B_0$ or $y \in B_1$ . Say $y \in B_0$ . Then $y \in B_{00}$ or $y \in B_{01}$ . Say, $y \in B_{01}$ . Now $y \in B_{010}$ or $y \in B_{011}$ . Say, $y \in B_{010}$ . Thus, we have:

$\displaystyle y \in B_0 \cap B_{01} \cap B_{010} \cap \cdots$

As a result, each $y \in C$ is associated with $h(y)$ , which is a sequence of countably infinite many zeros and ones such that the first $n$ coordinates of $h(y)$ agree with $g_n$ .

The mapping $h$ in the above paragraph is a bijection between the Cantor set $C$ and $S_{\omega}$ , the set of all countably infinite sequences of zeros and ones. If $g \in S_{\omega}$ , we let $g_n$ be the string of zeros and ones that agrees with the first $n$ coordinates of $g$ . Thus in this notation, for $y \in C$ , we have $\left\{y\right\}=\bigcap \limits_{n=1}^{\infty}B_{h(y)_n}$ .

To facilitate the subsequent discussion, we have the following lemma.

Lemma

For each $y \in C$ , the intervals $B_{h(y)_n}$ form a local base at $y$ , i.e. for each open interval $(a,b)$ with $y \in (a,b)$ , there is some integer $n$ such that $B_{h(y)_n} \subset (a,b)$ .
Let $D$ be the set of endpoints of the closed intervals $B_{g_n}$ obtained in the construction process. We have $D \subset C$ .
The set $D$ is dense in $C$ .

Proof
Condition 1 follows from the fact that the lengths of the closed intervals $B_{h(y)_n}$ go to zero.

We now prove condition 2. Let $B_{g_n}$ be a closed interval obtained in the construction process and let $s$ be the left endpoint and $t$ be the right endpoint. Both $s$ and $t$ belong to $C$ since:

$\displaystyle \left\{s\right\}=B_{g_n} \cap B_{g_n0} \cap B_{g_n00} \cap B_{g_n000} \cap \cdots$

$\displaystyle \left\{t\right\}=B_{g_n} \cap B_{g_n1} \cap B_{g_n11} \cap B_{g_n111} \cap \cdots$

The fact that $D$ is dense in $C$ follows from condition 1. Every open interval containing a point of $C$ has to contain one closed interval $B_{g_n}$ and thus the endpoints of $B_{g_n}$ . $\blacksquare$

Main Discussion
We discuss the following proeprties:

The Cantor set $C$ is a compact subset of $[0,1]$ .
The Cantor set $C$ is a perfect set.
$[0,1]-C$ , the complement of $C$ , is dense in $[0,1]$ .
The Cantor set $C$ contains no open interval.
The Cantor set $C$ is nowhere dense in $[0,1]$ .
The Cantor set $C$ is totally disconnected.

Discussion of 1
In the real line or in any other topological space, the intersection of closded sets is always a closed set. The Cantor set $C$ is the intersection of $A_n$ where each $A_n$ is a closed set (it being a finite union of closed intervals). Thus the Cantor set $C$ is a closed subset of $[0,1]$ . Being a closed and bounded subset of the real line, $C$ is compact. $\blacksquare$

Discussion of 2
Recall that a subset $W$ of the real line is a perfect set if it is closed and every point of $W$ is a limit point of $W$ . Let $y \in C$ . Let $(a,b)$ be an open interval of the real line such that $y \in (a,b)$ . We want to show that there are infinitely many points of $C$ inside $(a,b)$ . This following from condition 1 of the lemma. The interval $(a,b)$ contains $B_{g_n}$ which would contain infinitely many points in the Cantor set. Note that the construction process of the Cantor set would continue within the interval $B_{g_n}$ . $\blacksquare$

Discussion of 3
This also follows from condition 1 of the lemma. We need to demonstrate that every point in $[0,1]$ is either a point of $[0,1]-C$ or a limit point of $[0,1]-C$ . Let $y \in [0,1]$ . If $y \in [0,1]-C$ , then we are done. So suppose $y \in C$ . By condition 1 of the lemma, every open interval containing $y$ contains some closed interval $B_{g_n}$ . Since the middle third of $B_{g_n}$ is removed in the construction process, we see that $(a,b) \cap ([0,1]-C) \ne \phi$ . $\blacksquare$

Discussion of 4
This is a corollary of 3. Suppose we have $(a,b) \subset C$ . By 3, $(a,b)$ contains points of the removed open intervals, which is a contraction. $\blacksquare$

Discussion of 5
Let $A \subset \mathbb{R}$ . The set $A$ is nowhere dense in $\mathbb{R}$ if $A$ is dense in no open interval of $\mathbb{R}$ , or equivalently, for each open interval $(a,b)$ , there is some subinterval $(c,d) \subset (a,b)$ such that $(c,d) \cap A=\phi$ . To say that $A$ is nowhere dense in $[0,1]$ , we only need to concern with the open intervals that have points in $[0,1]$ .

This is a corollary of condition 4. For each open interval $(a,b)$ in $[0,1]$ , it cannot be a subset of $C$ . So there must some point $x \in (a,b)$ such that $x \notin C$ . But the Cantor set $C$ is a closed subset of $[0,1]$ . Then there must be some $(c,d) \subset (a,b)$ such that $x \in (c,d)$ and $(c,d) \cap C=\phi$ . $\blacksquare$

Discussion of 6
The Cantor set is totally disconnected. A subset $A$ of the real line $\mathbb{R}$ is a disconnected set if there are disjoint open sets $U$ and $V$ , both containing points of $A$ , such that $A=(U \cap A) \cup (V \cap A)$ . A set $A$ is connected if it is not disconnected.

The Cantor set $C$ is disconnected. Note that $C=([0,0.5) \cap C) \cup (0.5,1] \cap C)$ .

A set $A \subset \mathbb{R}$ is totally disconnected if the only connected subsets of $A$ are the singleton sets. We show that any subset of the Cantor set with at least two points is not connected. Let $A \subset C$ with $x,y \in A$ where $x<y$ . Since $C$ is nowhere dense, there exists $(c,d) \subset (x,y)$ such that $(c,d)$ has no points of $C$ . Let $t=0.5(c+d)$ . Then we have:

$\displaystyle A=([0,t) \cap A) \cup ((t,1] \cap A)$

The Cantor set, I

Posted on May 21, 2010 by Dan Ma

This is post # 6 of the series on the Euclidean topology of the real line. See the links at the bottom for other posts in the series.

The goal is this post is to construct the Cantor set and demonstrate that the Cantor set has the same cardinality as the set of all real numbers. In the next post we discuss the topological properties of the Cantor set.

The Construction
For each positive integer $n=1,2,3,\cdots$ , let $S_n$ be the set of all sequences zeros and ones of length $n$ . For example, $S_1=\{ 0,1 \}$ , $S_2=\{ 00, 01, 10, 11 \}$ , $S_3=\{000, 001, 010, 011, 100, 101, 110, 111 \}$ and so on. Each $S_n$ has $2^n$ sequences. For each $f \in S_n$ , we can tag on a $0$ or $1$ and obtain an element of $S_{n+1}$ . For example, for $011000 \in S_6$ , both $0110000, 0110001 \in S_7$ .

Let $A_0=[0,1]$ be the unit interval. Remove the middle third open interval $(\frac{1}{3},\frac{2}{3})$ from $A_0$ . Label the remaining two intervals by $B_0=[0,\frac{1}{3}]$ and $B_1=[\frac{2}{3},1]$ . Let $A_1=B_0 \cup B_1$ be the union of these two closed intervals.

Consider the stage at $n=2$ . For $0 \in S_1$ , remove the middle third of $B_0$ and obtain $B_{00}=[0,\frac{1}{9}]$ and $B_{01}=[\frac{2}{9},\frac{1}{3}]$ . For $1 \in S_1$ , remove the meddle third of $B_1$ and obtain $B_{10}=[\frac{2}{3},\frac{7}{9}]$ and $B_{11}=[\frac{8}{9},1]$ . Let $A_2=B_{00} \cup B_{01} \cup B_{10} \cup B_{11}$ . Note that the length of each closed interval $B_{ij}$ is $\displaystyle \frac{1}{3^2}=\frac{1}{9}$ .

Suppose we have the following at the $n^{th}$ stage, where $n \ge 1$ .

The closed interval $B_f$ has been defined for each $f \in S_n$ .
The length of each $B_f$ is $\frac{1}{3^n}$ .
$A_n=\bigcup \limits_{h \in S_n} B_h$ .

We now define the closed intervals in stage $n+1$ . For each closed interval $B_f$ , we remove the middle third open intervals and obtain two closed intervals $B_{f0}$ and $B_{f1}$ where each has length $\frac{1}{3^{n+1}}$ . Let $A_{n+1}$ be defined as:

$\displaystyle A_{n+1}=\bigcup \limits_{f \in S_n} (B_{f0} \cup B_{f1})=\bigcup \limits_{g \in S_{n+1}} B_g$

We now define the Cantor set $C=\bigcap \limits_{i=0}^{\infty} A_j$ . This is a nonempty set subset of the unit interval. The point $0 \in C$ since $0 \in B_0 \cap B_{00} \cap B_{000} \cap \cdots$ . Being the union of finitely many closed intervals, each $A_n$ is a closed subset of $[0,1]$ . Thus each $A_n$ is a compact subset of $[0,1]$ . Any nested decreasing sequence of compact subsets of the real line is nonempty. See the post The Euclidean topology of the real line (4) – Compactness. In the remainder of this post, we show that the Cantor set $C$ has the cardinality continuum.

General Discussion
Let $A$ and $B$ be sets. A function $f:A \rightarrow B$ is a one-to-one function if for $x,y \in A$ with $x \ne y$ , $f(x) \ne f(y)$ , that is, distinct elements of the domain are mapped to distinct elements of the range. A function $f:A \rightarrow B$ is said to be a surjection if $f(A)=B$ , i.e. every point in the set $B$ is mapped by some point of $A$ . A function $f:A \rightarrow B$ is said to be a bijection if it is both a one-to-one function and a surjection.

The sets $A$ and $B$ have the same cardinality if there is a bijection $f:A \rightarrow B$ . When $A$ and $B$ have the same cardinality, we use the notation $\lvert A \lvert=\lvert B \lvert$ . For example, the set of all rational numbers has the same cardinality as the integers since we can define a bijection between the two sets. More informally, we can put the rational numbers in an exhaustive list indexed by the integers. When a set has the same cadinality as the set of real numbers, we say that the set has cardinality continuum.

When there is a one-to-one function $f:A \rightarrow B$ , we denote this condition by $\lvert A \lvert \le \lvert B \lvert$ . Obviously when $A \subset B$ , we have $\lvert A \lvert \le \lvert B \lvert$ . The Cantor–Bernstein–Schroeder theorem states that when there are one-to-one functions $f:A \rightarrow B$ and $g:B \rightarrow A$ , we have $\lvert A \lvert=\lvert B \lvert$ . In other words, if $\lvert A \lvert \le \lvert B \lvert$ and $\lvert B \lvert \le \lvert A \lvert$ , we have $\lvert A \lvert=\lvert B \lvert$ . We utilize this fact when we show that the Cantor set and the set of all real numbers have the same cardinality.

The Cardinality of the Cantor Set
Let $\omega=\left\{0,1,2,3,\cdots\right\}$ be the set of all nonnegative integers. Let $S_{\omega}$ be the set of all infinite sequences of 0’s and 1’s. Let $\mathcal{P}(\omega)$ be the set of subsets of $\omega$ . The cardinality of the Cantor set follows from the following relationship:

$\displaystyle \lvert \mathbb{R} \lvert \le \lvert \mathcal{P}(\omega) \lvert = \lvert S_{\omega} \lvert = \lvert C \lvert \le \lvert \mathbb{R} \lvert$

The inequality $\lvert C \lvert \le \lvert \mathbb{R} \lvert$ is clear since the Cantor set is a subset of the real line. The following claims establish the relationship.

Claim 1 $\lvert S_{\omega} \lvert = \lvert C \lvert$
This follows from the contruction of the Cantor set. Let $y \in C$ . At each stage of the construction, there are $2^n$ many closed intervals and the point $y$ belongs to exactly one of these intervals, say $B_{f_n}$ . At the next stage, the point $y$ belongs to one of the closed intervals as a result of splitting $B_{f_n}$ by removing the middle third. Since the lengths of $B_{f_n}$ approaches to zero, we have $\left\{y\right\}=\bigcap \limits_{n=1}^{\infty} B_{f_n}$ .

Note that for each $f_n$ and $f_{n+1}$ agree on the first $n$ coordinates. Thus the finite sequences form an countably infinite sequence $f \in S_{\omega}$ such that $f$ and $f_n$ agree on the first $n$ coordinates of $f$ . Let $H(y)=f$ .

We just describe a mapping $H: C \rightarrow S_{\omega}$ . This mapping is one-to-one. For $x,y \in C$ where $x \ne y$ , there must be some stage $n$ where $x$ and $y$ belong to disjoint closed intervals. Otherwise, $x=y$ . Let $n$ be the least integer such that $x$ and $y$ belong to disjoint closed intervals. Then $x$ and $y$ belong to the same interval $B_{g}$ in stage $n-1$ . However, $x$ and $y$ belong to disjoint closed intervals at stage $n$ , say $x \in B_{g0}$ and $y \in B_{g1}$ . As a result, $H(x)$ and $H(y)$ disagree at the $n^{th}$ coordinate, implying $H(x) \ne H(y)$ .

No point in $S_{\omega}$ is missed by the mapping $H$ . For each $f \in S_{\omega}$ , let $f_n$ be the sequence of its first $n$ coordinates. Then the sequence of closed intervals $B_{f_n}$ collapses to a point $x$ . It is clear that $H(x)=f$ . $\blacksquare$

Claim 2 $\lvert \mathcal{P}(\omega) \lvert = \lvert S_{\omega} \lvert$
The surjection is defined by an indicator function. For each $A \in \mathcal{P}(\omega)$ , $F(A) \in S_{\omega}$ such that the $n^{th}$ coordinate $F(A)_n$ is:

$\displaystyle F(A)_n=\left\{\begin{matrix}0&\thinspace n \notin A \\{1}&\thinspace n \in A \end{matrix}\right.$

It can be verified that $F: \mathcal{P}(\omega) \rightarrow S_{\omega}$ is a one-to-one map and that $F(\mathcal{P}(\omega))=S_{\omega}$ . $\blacksquare$

Claim 3 $\lvert \mathbb{R} \lvert \le \lvert \mathcal{P}(\omega) \lvert$
Let $\mathbb{Q}$ be the set of all rational numbers. Since $\lvert \mathbb{Q} \lvert=\lvert \omega \lvert$ , we have $\lvert \mathcal{P}(\mathbb{Q}) \lvert=\lvert \mathcal{P}(\omega) \lvert$ . We now define a one-to-one map $G: \mathbb{R} \rightarrow \mathcal{P}(\mathbb{Q})$ .