The preceding post is an exercise showing that the product of countably many  -compact spaces is a Lindelof space. The result is an example of a situation where the Lindelof property is countably productive if each factor is a “nice” Lindelof space. In this case, “nice” means
-compact spaces is a Lindelof space. The result is an example of a situation where the Lindelof property is countably productive if each factor is a “nice” Lindelof space. In this case, “nice” means  -compact. This post gives several exercises surrounding the notion of
-compact. This post gives several exercises surrounding the notion of  -compactness.
-compactness.
Exercise 2.A
According to the preceding exercise, the product of countably many  -compact spaces is a Lindelof space. Give an example showing that the result cannot be extended to the product of uncountably many
-compact spaces is a Lindelof space. Give an example showing that the result cannot be extended to the product of uncountably many  -compact spaces. More specifically, give an example of a product of uncountably many
-compact spaces. More specifically, give an example of a product of uncountably many  -compact spaces such that the product space is not Lindelof.
-compact spaces such that the product space is not Lindelof.
Exercise 2.B
Any  -compact space is Lindelof. Since
-compact space is Lindelof. Since ![\mathbb{R}=\bigcup_{n=1}^\infty [-n,n]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BR%7D%3D%5Cbigcup_%7Bn%3D1%7D%5E%5Cinfty+%5B-n%2Cn%5D&bg=ffffff&fg=333333&s=0&c=20201002) , the real line with the usual Euclidean topology is
, the real line with the usual Euclidean topology is  -compact. This exercise is to find an example of “Lindelof does not imply
-compact. This exercise is to find an example of “Lindelof does not imply  -compact.” Find one such example among the subspaces of the real line. Note that as a subspace of the real line, the example would be a separable metric space, hence would be a Lindelof space.
-compact.” Find one such example among the subspaces of the real line. Note that as a subspace of the real line, the example would be a separable metric space, hence would be a Lindelof space.
Exercise 2.C
This exercise is also to look for an example of a space that is Lindelof and not  -compact. The example sought is a non-metric one, preferably a space whose underlying set is the real line and whose topology is finer than the Euclidean topology.
-compact. The example sought is a non-metric one, preferably a space whose underlying set is the real line and whose topology is finer than the Euclidean topology.
Exercise 2.D
Show that the product of two Lindelof spaces is a Lindelof space whenever one of the factors is a  -compact space.
-compact space.
Exercise 2.E
Prove that the product of finitely many  -compact spaces is a
-compact spaces is a  -compact space. Give an example of a space showing that the product of countably and infinitely many
-compact space. Give an example of a space showing that the product of countably and infinitely many  -compact spaces does not have to be
-compact spaces does not have to be  -compact. For example, show that
-compact. For example, show that  , the product of countably many copies of the real line, is not
, the product of countably many copies of the real line, is not  -compact.
-compact.
Comments
The Lindelof property and  -compactness are basic topological notions. The above exercises are natural questions based on these two basic notions. One immediate purpose of these exercises is that they provide further interaction with the two basic notions. More importantly, working on these exercise give exposure to mathematics that is seemingly unrelated to the two basic notions. For example, finding
-compactness are basic topological notions. The above exercises are natural questions based on these two basic notions. One immediate purpose of these exercises is that they provide further interaction with the two basic notions. More importantly, working on these exercise give exposure to mathematics that is seemingly unrelated to the two basic notions. For example, finding  -compactness on subspaces of the real line and subspaces of compact spaces naturally uses a Baire category argument, which is a deep and rich topic that finds uses in multiple areas of mathematics. For this reason, these exercises present excellent learning opportunities not only in topology but also in other useful mathematical topics.
-compactness on subspaces of the real line and subspaces of compact spaces naturally uses a Baire category argument, which is a deep and rich topic that finds uses in multiple areas of mathematics. For this reason, these exercises present excellent learning opportunities not only in topology but also in other useful mathematical topics.
If preferred, the exercises can be attacked head on. The exercises are also intended to be a guided tour. Hints are also provided below. Two sets of hints are given – Hints (blue dividers) and Further Hints (maroon dividers). The proofs of certain key facts are also given (orange dividers). Concluding remarks are given at the end of the post.






Hints for Exercise 2.A
Prove that the Lindelof property is hereditary with respect to closed subspaces. That is, if  is a Lindelof space, then every closed subspace of
is a Lindelof space, then every closed subspace of  is also Lindelof.
is also Lindelof.
Prove that if  is a Lindelof space, then every closed and discrete subset of
is a Lindelof space, then every closed and discrete subset of  is countable (every space that has this property is said to have countable extent).
is countable (every space that has this property is said to have countable extent).
Show that the product of uncountably many copies of the real line does not have countable extent. Specifically, focus on either one of the following two examples.
- Show that the product space
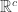 has a closed and discrete subspace of cardinality continuum where
has a closed and discrete subspace of cardinality continuum where  is cardinality of continuum. Hence
is cardinality of continuum. Hence 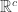 is not Lindelof.
is not Lindelof.
- Show that the product space
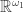 has a closed and discrete subspace of cardinality
has a closed and discrete subspace of cardinality  where
where  is the first uncountable ordinal. Hence
is the first uncountable ordinal. Hence 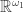 is not Lindelof.
is not Lindelof.
Hints for Exercise 2.B
Let  be the set of all irrational numbers. Show that
be the set of all irrational numbers. Show that  as a subspace of the real line is not
as a subspace of the real line is not  -compact.
-compact.
Hints for Exercise 2.C
Let  be the real line with the topology generated by the half open and half closed intervals of the form
be the real line with the topology generated by the half open and half closed intervals of the form 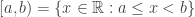 . The real line with this topology is called the Sorgenfrey line. Show that
. The real line with this topology is called the Sorgenfrey line. Show that  is Lindelof and is not
is Lindelof and is not  -compact.
-compact.
Hints for Exercise 2.D
It is helpful to first prove: the product of two Lindelof space is Lindelof if one of the factors is a compact space. The Tube lemma is helpful.
Tube Lemma
Let  be a space. Let
be a space. Let  be a compact space. Suppose that
be a compact space. Suppose that  is an open subset of
is an open subset of  and suppose that
and suppose that  where
where 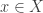 . Then there exists an open subset
. Then there exists an open subset  of
of  such that
such that 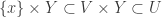 .
.
Hints for Exercise 2.E
Since the real line  is homeomorphic to the open interval
is homeomorphic to the open interval 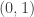 ,
,  is homeomorphic to
is homeomorphic to  . Show that
. Show that  is not
is not  -compact.
-compact.






Further Hints for Exercise 2.A
The hints here focus on the example 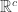 .
.
Let ![I=[0,1]](https://s0.wp.com/latex.php?latex=I%3D%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Let
. Let  be the first infinite ordinal. For convenience, consider
be the first infinite ordinal. For convenience, consider  the set
the set 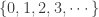 , the set of all non-negative integers. Since
, the set of all non-negative integers. Since  is a closed subset of
is a closed subset of 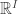 , any closed and discrete subset of
, any closed and discrete subset of  is a closed and discrete subset of
is a closed and discrete subset of 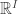 . The task at hand is to find a closed and discrete subset of
. The task at hand is to find a closed and discrete subset of  . To this end, we define
. To this end, we define  after setting up background information.
after setting up background information.
For each 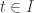 , choose a sequence
, choose a sequence 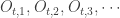 of open intervals (in the usual topology of
of open intervals (in the usual topology of  ) such that
) such that
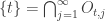 ,
,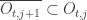 for each
for each  (the closure is in the usual topology of
(the closure is in the usual topology of  ).
).
Note. For each 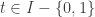 , the open intervals
, the open intervals 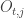 are of the form
are of the form 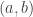 . For
. For 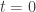 , the open intervals
, the open intervals 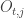 are of the form
are of the form  . For
. For 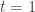 , the open intervals
, the open intervals 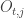 are of the form
are of the form ![(a,1]](https://s0.wp.com/latex.php?latex=%28a%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
For each 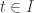 , define the map
, define the map 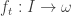 as follows:
as follows:
We are now ready to define  . For each
. For each 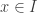 ,
,  is the mapping
is the mapping 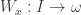 defined by
defined by 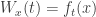 for each
for each 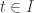 .
.
Show the following:
- The set
 has cardinality continuum.
has cardinality continuum.
- The set
 is a discrete space.
is a discrete space.
- The set
 is a closed subspace of
is a closed subspace of  .
.
Further Hints for Exercise 2.B
A subset  of the real line
of the real line  is nowhere dense in
is nowhere dense in  if for any nonempty open subset
if for any nonempty open subset  of
of  , there is a nonempty open subset
, there is a nonempty open subset  of
of  such that
such that  . If we replace open sets by open intervals, we have the same notion.
. If we replace open sets by open intervals, we have the same notion.
Show that the real line  with the usual Euclidean topology cannot be the union of countably many closed and nowhere dense sets.
with the usual Euclidean topology cannot be the union of countably many closed and nowhere dense sets.
Further Hints for Exercise 2.C
Prove that if  and
and  are
are  -compact, then the product
-compact, then the product  is
is  -compact, hence Lindelof.
-compact, hence Lindelof.
Prove that  , the Sorgenfrey line, is Lindelof while its square
, the Sorgenfrey line, is Lindelof while its square  is not Lindelof.
is not Lindelof.
Further Hints for Exercise 2.D
As suggested in the hints given earlier, prove that  is Lindelof if
is Lindelof if  is Lindelof and
is Lindelof and  is compact. As suggested, the Tube lemma is a useful tool.
is compact. As suggested, the Tube lemma is a useful tool.
Further Hints for Exercise 2.E
The product space  is a subspace of the product space
is a subspace of the product space ![[0,1]^\omega](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%5E%5Comega&bg=ffffff&fg=333333&s=0&c=20201002) . Since
. Since ![[0,1]^\omega](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%5E%5Comega&bg=ffffff&fg=333333&s=0&c=20201002) is compact, we can fall back on a Baire category theorem argument to show why
is compact, we can fall back on a Baire category theorem argument to show why  cannot be
cannot be  -compact. To this end, we consider the notion of Baire space. A space
-compact. To this end, we consider the notion of Baire space. A space  is said to be a Baire space if for each countable family
is said to be a Baire space if for each countable family 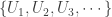 of open and dense subsets of
of open and dense subsets of  , the intersection
, the intersection 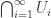 is a dense subset of
is a dense subset of  . Prove the following results.
. Prove the following results.
Fact E.1
Let  be a compact Hausdorff space. Let
be a compact Hausdorff space. Let 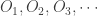 be a sequence of non-empty open subsets of
be a sequence of non-empty open subsets of  such that
such that 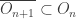 for each
for each  . Then the intersection
. Then the intersection  is non-empty.
is non-empty.
Fact E.2
Any compact Hausdorff space is Baire space.
Fact E.3
Let  be a Baire space. Let
be a Baire space. Let  be a dense
be a dense  -subset of
-subset of  such that
such that 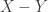 is a dense subset of
is a dense subset of  . Then
. Then  is not a
is not a  -compact space.
-compact space.
Since ![X=[0,1]^\omega](https://s0.wp.com/latex.php?latex=X%3D%5B0%2C1%5D%5E%5Comega&bg=ffffff&fg=333333&s=0&c=20201002) is compact, it follows from Fact E.2 that the product space
is compact, it follows from Fact E.2 that the product space ![X=[0,1]^\omega](https://s0.wp.com/latex.php?latex=X%3D%5B0%2C1%5D%5E%5Comega&bg=ffffff&fg=333333&s=0&c=20201002) is a Baire space.
is a Baire space.
Fact E.4
Let ![X=[0,1]^\omega](https://s0.wp.com/latex.php?latex=X%3D%5B0%2C1%5D%5E%5Comega&bg=ffffff&fg=333333&s=0&c=20201002) and
and  . The product space
. The product space  is a dense
is a dense  -subset of
-subset of ![X=[0,1]^\omega](https://s0.wp.com/latex.php?latex=X%3D%5B0%2C1%5D%5E%5Comega&bg=ffffff&fg=333333&s=0&c=20201002) . Furthermore,
. Furthermore, 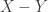 is a dense subset of
is a dense subset of  .
.
It follows from the above facts that the product space  cannot be a
cannot be a  -compact space.
-compact space.






Proofs of Key Steps for Exercise 2.A
The proof here focuses on the example 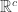 .
.
To see that  has the same cardinality as that of
has the same cardinality as that of  , show that
, show that  for
for  . This follows from the definition of the mapping
. This follows from the definition of the mapping  .
.
To see that  is discrete, for each
is discrete, for each 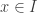 , consider the open set
, consider the open set  . Note that
. Note that 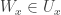 . Further note that
. Further note that 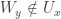 for all
for all 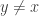 .
.
To see that  is a closed subset of
is a closed subset of  , let
, let  such that
such that 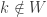 . Consider two cases.
. Consider two cases.
Case 1. 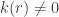 for all
for all  .
.
Note that 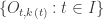 is an open cover of
is an open cover of  (in the usual topology). There exists a finite
(in the usual topology). There exists a finite 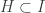 such that
such that  is a cover of
is a cover of  . Consider the open set
. Consider the open set 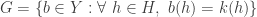 . Define the set
. Define the set  as follows:
as follows:
The set  can be further described as follows:
can be further described as follows:
The last step is  because
because  is a cover of
is a cover of  . The fact that
. The fact that 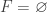 means that
means that  is an open subset of
is an open subset of  containing the point
containing the point  such that
such that  contains no point of
contains no point of  .
.
Case 2. 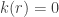 for some
for some  .
.
Since 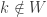 ,
, 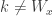 for all
for all 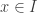 . In particular,
. In particular,  . This means that
. This means that 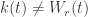 for some
for some 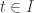 . Define the open set
. Define the open set  as follows:
as follows:
Clearly  . Observe that
. Observe that 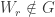 since
since  . For each
. For each  ,
, 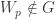 since
since  . Thus
. Thus  is an open set containing
is an open set containing  such that
such that 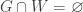 .
.
Both cases show that  is a closed subset of
is a closed subset of  .
.
Proofs of Key Steps for Exercise 2.B
Suppose that  , the set of all irrational numbers, is
, the set of all irrational numbers, is  -compact. That is,
-compact. That is, 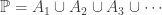 where each
where each 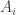 is a compact space as a subspace of
is a compact space as a subspace of  . Any compact subspace of
. Any compact subspace of  is also a compact subspace of
is also a compact subspace of  . As a result, each
. As a result, each 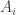 is a closed subset of
is a closed subset of  . Furthermore, prove the following:
. Furthermore, prove the following:
Each 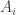 is a nowhere dense subset of
is a nowhere dense subset of  .
.
Each singleton set 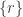 where
where  is any rational number is also a closed and nowhere dense subset of
is any rational number is also a closed and nowhere dense subset of  . This means that the real line is the union of countably many closed and nowhere dense subsets, contracting the hints given earlier. Thus
. This means that the real line is the union of countably many closed and nowhere dense subsets, contracting the hints given earlier. Thus  cannot be
cannot be  -compact.
-compact.
Proofs of Key Steps for Exercise 2.C
The Sorgenfrey line  is a Lindelof space whose square
is a Lindelof space whose square  is not normal. This is a famous example of a Lindelof space whose square is not Lindelof (not even normal). For reference, a proof is found here. An alternative proof of the non-normality of
is not normal. This is a famous example of a Lindelof space whose square is not Lindelof (not even normal). For reference, a proof is found here. An alternative proof of the non-normality of  uses the Baire category theorem and is found here.
uses the Baire category theorem and is found here.
If the Sorgenfrey line is  -compact, then
-compact, then  would be
would be  -compact and hence Lindelof. Thus
-compact and hence Lindelof. Thus  cannot be
cannot be  -compact.
-compact.
Proofs of Key Steps for Exercise 2.D
Suppose that  is Lindelof and that
is Lindelof and that  is compact. Let
is compact. Let  be an open cover of
be an open cover of  . For each
. For each 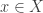 , let
, let 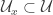 be finite such that
be finite such that 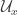 is a cover of
is a cover of  . Putting it another way,
. Putting it another way, 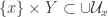 . By the Tube lemma, for each
. By the Tube lemma, for each 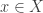 , there is an open
, there is an open 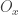 such that
such that 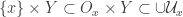 . Since
. Since  is Lindelof, there exists a countable set
is Lindelof, there exists a countable set 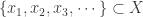 such that
such that 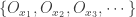 is a cover of
is a cover of  . Then
. Then 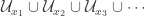 is a countable subcover of
is a countable subcover of  . This completes the proof that
. This completes the proof that  is Lindelof when
is Lindelof when  is Lindelof and
is Lindelof and  is compact.
is compact.
To complete the exercise, observe that if  is Lindelof and
is Lindelof and  is
is  -compact, then
-compact, then  is the union of countably many Lindelof subspaces.
is the union of countably many Lindelof subspaces.
Proofs of Key Steps for Exercise 2.E
Proof of Fact E.1
Let  be a compact Hausdorff space. Let
be a compact Hausdorff space. Let 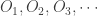 be a sequence of non-empty open subsets of
be a sequence of non-empty open subsets of  such that $latex
such that $latex 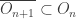 for each
for each  . Show that the intersection
. Show that the intersection  is non-empty.
is non-empty.
Suppose that  . Choose
. Choose  . There must exist some
. There must exist some 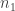 such that
such that 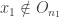 . Choose
. Choose 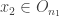 . There must exist some
. There must exist some 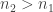 such that
such that 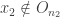 . Continue in this manner we can choose inductively an infinite set
. Continue in this manner we can choose inductively an infinite set 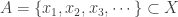 such that
such that 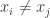 for
for  . Since
. Since  is compact, the infinite set
is compact, the infinite set  has a limit point
has a limit point  . This means that every open set containing
. This means that every open set containing  contains some
contains some 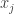 (in fact for infinitely many
(in fact for infinitely many  ). The point
). The point  cannot be in the intersection
cannot be in the intersection  . Thus for some
. Thus for some  ,
,  . Thus
. Thus 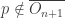 . We can choose an open set
. We can choose an open set  such that
such that  and
and 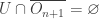 . However,
. However,  must contain some point
must contain some point 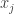 where
where 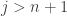 . This is a contradiction since
. This is a contradiction since  for all
for all 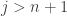 . Thus Fact E.1 is established.
. Thus Fact E.1 is established.
Proof of Fact E.2
Let  be a compact space. Let
be a compact space. Let 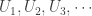 be open subsets of
be open subsets of  such that each
such that each 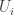 is also a dense subset of
is also a dense subset of  . Let
. Let  a non-empty open subset of
a non-empty open subset of  . We wish to show that
. We wish to show that  contains a point that belongs to each
contains a point that belongs to each 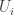 . Since
. Since 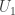 is dense in
is dense in  ,
,  is non-empty. Since
is non-empty. Since 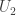 is dense in
is dense in  , choose non-empty open
, choose non-empty open  such that
such that 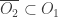 and
and 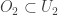 . Since
. Since  is dense in
is dense in  , choose non-empty open
, choose non-empty open 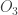 such that
such that  and
and 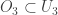 . Continue inductively in this manner and we have a sequence of open sets
. Continue inductively in this manner and we have a sequence of open sets 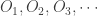 just like in Fact E.1. Then the intersection of the open sets
just like in Fact E.1. Then the intersection of the open sets  is non-empty. Points in the intersection are in
is non-empty. Points in the intersection are in  and in all the
and in all the 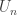 . This completes the proof of Fact E.2.
. This completes the proof of Fact E.2.
Proof of Fact E.3
Let  be a Baire space. Let
be a Baire space. Let  be a dense
be a dense  -subset of
-subset of  such that
such that 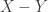 is a dense subset of
is a dense subset of  . Show that
. Show that  is not a
is not a  -compact space.
-compact space.
Suppose  is
is  -compact. Let
-compact. Let  where each
where each 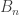 is compact. Each
is compact. Each 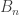 is obviously a closed subset of
is obviously a closed subset of  . We claim that each
. We claim that each 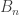 is a closed nowhere dense subset of
is a closed nowhere dense subset of  . To see this, let
. To see this, let  be a non-empty open subset of
be a non-empty open subset of  . Since
. Since 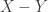 is dense in
is dense in  ,
,  contains a point
contains a point  where
where  . Since
. Since 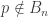 , there exists a non-empty open
, there exists a non-empty open 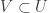 such that
such that 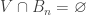 . This shows that each
. This shows that each 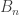 is a nowhere dense subset of
is a nowhere dense subset of  .
.
Since  is a dense
is a dense  -subset of
-subset of  ,
,  where each
where each  is an open and dense subset of
is an open and dense subset of  . Then each
. Then each 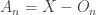 is a closed nowhere dense subset of
is a closed nowhere dense subset of  . This means that
. This means that  is the union of countably many closed and nowhere dense subsets of
is the union of countably many closed and nowhere dense subsets of  . More specifically, we have the following.
. More specifically, we have the following.
(1)………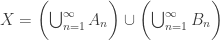
Statement (1) contradicts the fact that  is a Baire space. Note that all
is a Baire space. Note that all 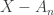 and
and 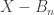 are open and dense subsets of
are open and dense subsets of  . Further note that the intersection of all these countably many open and dense subsets of
. Further note that the intersection of all these countably many open and dense subsets of  is empty according to (1). Thus
is empty according to (1). Thus  cannot not a
cannot not a  -compact space.
-compact space.
Proof of Fact E.4
The space ![X=[0,1]^\omega](https://s0.wp.com/latex.php?latex=X%3D%5B0%2C1%5D%5E%5Comega&bg=ffffff&fg=333333&s=0&c=20201002) is compact since it is a product of compact spaces. To see that
is compact since it is a product of compact spaces. To see that  is a dense
is a dense  -subset of
-subset of  , note that
, note that 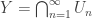 where for each integer
where for each integer 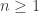
(2)………![U_n=(0,1) \times \cdots \times (0,1) \times [0,1] \times [0,1] \times \cdots](https://s0.wp.com/latex.php?latex=U_n%3D%280%2C1%29+%5Ctimes+%5Ccdots+%5Ctimes+%280%2C1%29+%5Ctimes+%5B0%2C1%5D+%5Ctimes+%5B0%2C1%5D+%5Ctimes+%5Ccdots&bg=ffffff&fg=333333&s=0&c=20201002)
Note that the first  factors of
factors of 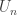 are the open interval
are the open interval 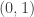 and the remaining factors are the closed interval
and the remaining factors are the closed interval ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) . It is also clear that
. It is also clear that 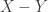 is a dense subset of
is a dense subset of  . This completes the proof of Fact E.4.
. This completes the proof of Fact E.4.






Concluding Remarks
Exercise 2.A
The exercise is to show that the product of uncountably many  -compact spaces does not need to be Lindelof. The approach suggested in the hints is to show that
-compact spaces does not need to be Lindelof. The approach suggested in the hints is to show that 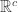 has uncountable extent where
has uncountable extent where  is continuum. Having uncountable extent (i.e. having an uncountable subset that is both closed and discrete) implies the space is not Lindelof. The uncountable extent of the product space
is continuum. Having uncountable extent (i.e. having an uncountable subset that is both closed and discrete) implies the space is not Lindelof. The uncountable extent of the product space 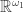 is discussed in this post.
is discussed in this post.
For 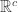 and
and 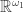 , there is another way to show non-Lindelof. For example, both product spaces are not normal. As a result, both product spaces cannot be Lindelof. Note that every regular Lindelof space is normal. Both product spaces contain the product
, there is another way to show non-Lindelof. For example, both product spaces are not normal. As a result, both product spaces cannot be Lindelof. Note that every regular Lindelof space is normal. Both product spaces contain the product  as a closed subspace. The non-normality of
as a closed subspace. The non-normality of  is discussed here.
is discussed here.
Exercise 2.B
The hints given above is to show that the set of all irrational numbers,  , is not
, is not  -compact (as a subspace of the real line). The same argument showing that
-compact (as a subspace of the real line). The same argument showing that  is not
is not  -compact can be generalized. Note that the complement of
-compact can be generalized. Note that the complement of  is
is 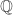 , the set of all rational numbers (a countable set). In this case,
, the set of all rational numbers (a countable set). In this case, 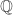 is a dense subset of the real line and is the union of countably many singleton sets. Each singleton set is a closed and nowhere dense subset of the real line. In general, we can let
is a dense subset of the real line and is the union of countably many singleton sets. Each singleton set is a closed and nowhere dense subset of the real line. In general, we can let  , the complement of a set
, the complement of a set  , be dense in the real line and be the union of countably many closed nowhere dense subsets of the real line (not necessarily singleton sets). The same argument will show that
, be dense in the real line and be the union of countably many closed nowhere dense subsets of the real line (not necessarily singleton sets). The same argument will show that  cannot be a
cannot be a  -compact space. This argument is captured in Fact E.3 in Exercise 2.E. Thus both Exercise 2.B and Exercise 2.E use a Baire category argument.
-compact space. This argument is captured in Fact E.3 in Exercise 2.E. Thus both Exercise 2.B and Exercise 2.E use a Baire category argument.
Exercise 2.E
Like Exercise 2.B, this exercise is also to show a certain space is not  -compact. In this case, the suggested space is
-compact. In this case, the suggested space is  , the product of countably many copies of the real line. The hints given use a Baire category argument, as outlined in Fact E.1 through Fact E.4. The product space
, the product of countably many copies of the real line. The hints given use a Baire category argument, as outlined in Fact E.1 through Fact E.4. The product space  is embedded in the compact space
is embedded in the compact space ![[0,1]^{\omega}](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%5E%7B%5Comega%7D&bg=ffffff&fg=333333&s=0&c=20201002) , which is a Baire space. As mentioned earlier, Fact E.3 is essentially the same argument used for Exercise 2.B.
, which is a Baire space. As mentioned earlier, Fact E.3 is essentially the same argument used for Exercise 2.B.
Using the same Baire category argument, it can be shown that  , the product of countably many copies of the countably infinite discrete space, is not
, the product of countably many copies of the countably infinite discrete space, is not  -compact. The space
-compact. The space  of the non-negative integers, as a subspace of the real line, is certainly
of the non-negative integers, as a subspace of the real line, is certainly  -compact. Using the same Baire category argument, we can see that the product of countably many copies of this discrete space is not
-compact. Using the same Baire category argument, we can see that the product of countably many copies of this discrete space is not  -compact. With the product space
-compact. With the product space  , there is a connection with Exercise 2.B. The product
, there is a connection with Exercise 2.B. The product  is homeomorphic to
is homeomorphic to  . The idea of the homeomorphism is discussed here. Thus the non-
. The idea of the homeomorphism is discussed here. Thus the non- -compactness of
-compactness of  can be achieved by mapping it to the irrationals. Of course, the same Baire category argument runs through both exercises.
can be achieved by mapping it to the irrationals. Of course, the same Baire category argument runs through both exercises.
Exercise 2.C
Even the non- -compactness of the Sorgenfrey line
-compactness of the Sorgenfrey line  can be achieved by a Baire category argument. The non-normality of the Sorgenfrey plane
can be achieved by a Baire category argument. The non-normality of the Sorgenfrey plane  can be achieved by Jones’ lemma argument or by the fact that
can be achieved by Jones’ lemma argument or by the fact that  is not a first category set. Links to both arguments are given in the Proof section above.
is not a first category set. Links to both arguments are given in the Proof section above.
See here for another introduction to the Baire category theorem.
The Tube lemma is discussed here.



Dan Ma topology
Daniel Ma topology
Dan Ma math
Daniel Ma mathematics
 2019 – Dan Ma
2019 – Dan Ma
be a mapping from a topological space
onto a topological space
. If
is a perfect map and
is a Lindelof space, then so is
. If
is a closed map and
is a paracompact space, then so is
. In other words, the pre-image of a Lindelof space under a perfect map is always a Lindelof space. Likewise, the pre-image of a paracompact space under a closed map is always a paracompact space. After proving these two facts, we show that for any compact space
, the product
is Lindelof (paracompact) for any Lindelof (paracompact) space
. All spaces under consideration are Hausdorff.
if the following holds: for any mapping
belonging to
, if
has the property, then so does
. In contrast, a topological property is an invariance of a class of mappings
if for any mapping
belonging to
, if
has the property, then so does
.
, where
, is a closed map if for any closed subset
of
,
is closed in
. A mapping
, where
, is a perfect map if
is a closed map and that the point inverse
is compact for each
.
be a closed map with
. Let
be an open subset of
. Define
. Then the set
is open in
and that
.
be a perfect map with
. Suppose
is Lindelof. Let
be an open cover of
. Without loss of generality, we can assume that
is closed under finite unions. For each
, define
. By Lemma 3, each
is an open subset of
. We claim that
is an open cover of
. To this end, let
. Since
is a perfect map, the point inverse
is compact. As a result, we can find a finite
such that
. Since
is closed under finite unions,
. It follows that
. Since
is Lindelof, there exists a countable
such that
. For each
,
for some
. We claim that
is a cover of
. To this end, let
. Then for some
,
. This implies that
. Thus, the open cover
has a countable subcover. This concludes the proof of Theorem 1.
be a perfect map with
. Suppose
is paracompact. Let
be an open cover of
. For each
, define
as in Lemma 3. By Lemma 3, each
is an open subset of
. Let
. As shown in the proof of Theorem 1,
is an open cover of
. Since
is paracompact, there exists a locally finite open refinement
of
. Let
.
. (1) It is an open cover of
. (2) It is a locally finite collection in
. (3) It is a refinement of
. To see (1), note that
is an open cover of
. As a result,
is an open cover of
. To see (2), let
. We find an open
such that
and such that
intersects only finitely many elements of
. Since
is locally finite in
, there exists an open
such that
and such that
intersects only finitely many elements of
, say,
. Let
. Clearly,
. It can be verified that the only elements of
having non-empty intersections with
are
,
,
. To see (3), let
where
. Then
for some
and some
. We claim that
. Let
. Then
. This implies that
. It follows that
is a locally finite open refinement of the open cover
. This completes the proof of Theorem 2.
is productively paramcompact if
is paracompact for every paracompact space
. The definition for productively Lindelof can be stated in a similar way. For some reason, the term “productively paracompact” is not used in the literature but is a topic that had been extensively studied. It is also a topic found in this site. The following four classes of spaces are productively paracompact (see here and here).
-compact spaces
-locally compact spaces
any compact space. Then
is Lindelof for every Lindelof space
.
any compact space. Then
is paracompact for every paracompact space
.
is compact. Then the projection map from
onto
is a closed map. The paracompactness of
follows whenever
is paracompact. The projection map is also perfect since the point inverses are compact due to the compactness of the factor
. Then the Lindelofness of
follows whenever
is Lindelof.
2023 – Dan Ma

