Let  be the first uncountable ordinal. The topology on
be the first uncountable ordinal. The topology on  we are interested in is the ordered topology, the topology induced by the well ordering. The space
we are interested in is the ordered topology, the topology induced by the well ordering. The space  is also called the space of all countable ordinals since it consists of all ordinals that are countable in cardinality. It is a handy example of a countably compact space that is not compact. In this post, we consider normality in the powers of
is also called the space of all countable ordinals since it consists of all ordinals that are countable in cardinality. It is a handy example of a countably compact space that is not compact. In this post, we consider normality in the powers of  . We also make comments on normality in the powers of a countably compact non-compact space.
. We also make comments on normality in the powers of a countably compact non-compact space.
Let  be the first infinite ordinal. It is well known that
be the first infinite ordinal. It is well known that  , the product space of
, the product space of  many copies of
many copies of  , is not normal (a proof can be found in this earlier post). This means that any product space
, is not normal (a proof can be found in this earlier post). This means that any product space 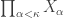 , with uncountably many factors, is not normal as long as each factor
, with uncountably many factors, is not normal as long as each factor  contains a countable discrete space as a closed subspace. Thus in order to discuss normality in the product space
contains a countable discrete space as a closed subspace. Thus in order to discuss normality in the product space 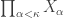 , the interesting case is when each factor is infinite but contains no countable closed discrete subspace (i.e. no closed copies of
, the interesting case is when each factor is infinite but contains no countable closed discrete subspace (i.e. no closed copies of  ). In other words, the interesting case is that each factor
). In other words, the interesting case is that each factor  is a countably compact space that is not compact (see this earlier post for a discussion of countably compactness). In particular, we would like to discuss normality in
is a countably compact space that is not compact (see this earlier post for a discussion of countably compactness). In particular, we would like to discuss normality in  where
where  is a countably non-compact space. In this post we start with the space
is a countably non-compact space. In this post we start with the space  of the countable ordinals. We examine
of the countable ordinals. We examine  power
power 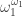 as well as the countable power
as well as the countable power  . The former is not normal while the latter is normal. The proof that
. The former is not normal while the latter is normal. The proof that  is normal is an application of the normality of
is normal is an application of the normality of 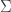 -product of the real line.
-product of the real line.
____________________________________________________________________
The uncountable product
Theorem 1
The product space 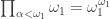 is not normal.
is not normal.
Theorem 1 follows from Theorem 2 below. For any space  , a collection
, a collection  of subsets of
of subsets of  is said to have the finite intersection property if for any finite
is said to have the finite intersection property if for any finite 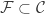 , the intersection
, the intersection 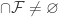 . Such a collection
. Such a collection  is called an f.i.p collection for short. It is well known that a space
is called an f.i.p collection for short. It is well known that a space  is compact if and only collection
is compact if and only collection  of closed subsets of
of closed subsets of  satisfying the finite intersection property has non-empty intersection (see Theorem 1 in this earlier post). Thus any non-compact space has an f.i.p. collection of closed sets that have empty intersection.
satisfying the finite intersection property has non-empty intersection (see Theorem 1 in this earlier post). Thus any non-compact space has an f.i.p. collection of closed sets that have empty intersection.
In the space  , there is an f.i.p. collection of cardinality
, there is an f.i.p. collection of cardinality  using its linear order. For each
using its linear order. For each  , let
, let  . Let
. Let  . It is a collection of closed subsets of
. It is a collection of closed subsets of  . It is an f.i.p. collection and has empty intersection. It turns out that for any countably compact space
. It is an f.i.p. collection and has empty intersection. It turns out that for any countably compact space  with an f.i.p. collection of cardinality
with an f.i.p. collection of cardinality  that has empty intersection, the product space
that has empty intersection, the product space  is not normal.
is not normal.
Theorem 2
Let  be a countably compact space. Suppose that there exists a collection
be a countably compact space. Suppose that there exists a collection  of closed subsets of
of closed subsets of  such that
such that  has the finite intersection property and that
has the finite intersection property and that  has empty intersection. Then the product space
has empty intersection. Then the product space  is not normal.
is not normal.
Proof of Theorem 2
Let’s set up some notations on product space that will make the argument easier to follow. By a standard basic open set in the product space 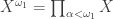 , we mean a set of the form
, we mean a set of the form  such that each
such that each 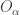 is an open subset of
is an open subset of  and that
and that  for all but finitely many
for all but finitely many  . Given a standard basic open set
. Given a standard basic open set  , the notation
, the notation 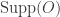 refers to the finite set of
refers to the finite set of  for which
for which  . For any set
. For any set  , the notation
, the notation 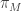 refers to the projection map from
refers to the projection map from  to the subproduct
to the subproduct  . Each element
. Each element 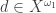 can be considered a function
can be considered a function 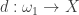 . By
. By  , we mean
, we mean  .
.
For each  , let
, let  be the constant function whose constant value is
be the constant function whose constant value is  . Consider the following subspaces of
. Consider the following subspaces of  .
.
Both  and
and  are closed subsets of the product space
are closed subsets of the product space  . Because the collection
. Because the collection  has empty intersection,
has empty intersection, 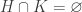 . We show that
. We show that  and
and  cannot be separated by disjoint open sets. To this end, let
cannot be separated by disjoint open sets. To this end, let  and
and  be open subsets of
be open subsets of  such that
such that  and
and  .
.
Let  . Choose a standard basic open set
. Choose a standard basic open set 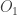 such that
such that  . Let
. Let  . Since
. Since 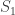 is the support of
is the support of 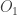 , it follows that
, it follows that 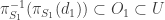 . Since
. Since  has the finite intersection property, there exists
has the finite intersection property, there exists 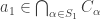 .
.
Define  such that
such that  for all
for all 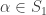 and
and  for all
for all  . Choose a standard basic open set
. Choose a standard basic open set  such that
such that  . Let
. Let  . It is possible to ensure that
. It is possible to ensure that  by making more factors of
by making more factors of  different from
different from  . We have
. We have 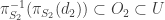 . Since
. Since  has the finite intersection property, there exists
has the finite intersection property, there exists  .
.
Now choose a point 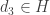 such that
such that 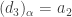 for all
for all 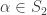 and
and  for all
for all  . Continue on with this inductive process. When the inductive process is completed, we have the following sequences:
. Continue on with this inductive process. When the inductive process is completed, we have the following sequences:
- a sequence
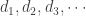 of point of
of point of  ,
,
- a sequence
 of finite subsets of
of finite subsets of  ,
,
- a sequence
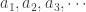 of points of
of points of 
such that for all 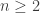 ,
,  for all
for all  and
and 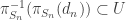 . Let
. Let  . Either
. Either  is finite or
is finite or  is infinite. Let’s examine the two cases.
is infinite. Let’s examine the two cases.
Case 1
Suppose that  is infinite. Since
is infinite. Since  is countably compact,
is countably compact,  has a limit point
has a limit point  . That means that every open set containing
. That means that every open set containing  contains some
contains some 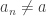 . For each
. For each 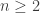 , define
, define  such that
such that
From the induction step, we have  for all
for all  . Let
. Let  , the constant function whose constant value is
, the constant function whose constant value is  . It follows that
. It follows that  is a limit of
is a limit of 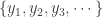 . This means that
. This means that  . Since
. Since  ,
,  .
.
Case 2
Suppose that  is finite. Then there is some
is finite. Then there is some  such that
such that  for all
for all 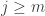 . For each
. For each 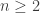 , define
, define  such that
such that
As in Case 1, we have  for all
for all  . Let
. Let  , the constant function whose constant value is
, the constant function whose constant value is 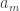 . It follows that
. It follows that  for all
for all 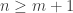 . Thus
. Thus  .
.
Both cases show that  . This completes the proof the product space
. This completes the proof the product space  is not normal.
is not normal. 
____________________________________________________________________
The countable product
Theorem 3
The product space  is normal.
is normal.
Proof of Theorem 3
The proof here actually proves more than normality. It shows that  is collectionwise normal, which is stronger than normality. The proof makes use of the
is collectionwise normal, which is stronger than normality. The proof makes use of the 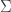 -product of
-product of  many copies of
many copies of  , which is the following subspace of the product space
, which is the following subspace of the product space  .
.
It is well known that  is collectionwise normal (see this earlier post). We show that
is collectionwise normal (see this earlier post). We show that  is a closed subspace of
is a closed subspace of  where
where 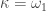 . Thus
. Thus  is collectionwise normal. This is established in the following claims.
is collectionwise normal. This is established in the following claims.
Claim 1
We show that the space  is embedded as a closed subspace of
is embedded as a closed subspace of 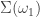 .
.
For each  , define
, define  such that
such that 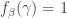 for all
for all  and
and  for all
for all  . Let
. Let  . We show that
. We show that  is a closed subset of
is a closed subset of 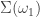 and
and  is homeomorphic to
is homeomorphic to  according to the mapping
according to the mapping  .
.
First, we show  is closed by showing that
is closed by showing that  is open. Let
is open. Let 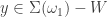 . We show that there is an open set containing
. We show that there is an open set containing  that contains no points of
that contains no points of  .
.
Suppose that for some 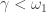 ,
,  . Consider the open set
. Consider the open set  where
where 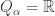 except that
except that  . Then
. Then  and
and  .
.
So we can assume that for all 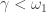 ,
,  . There must be some
. There must be some  such that
such that 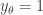 . Otherwise,
. Otherwise, 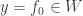 . Since
. Since 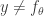 , there must be some
, there must be some  such that
such that 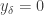 . Now choose the open interval
. Now choose the open interval  and the open interval
and the open interval  . Consider the open set
. Consider the open set 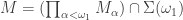 such that
such that  except for
except for  and
and  . Then
. Then  and
and  . We have just established that
. We have just established that  is closed in
is closed in 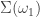 .
.
Consider the mapping  . Based on how it is defined, it is straightforward to show that it is a homeomorphism between
. Based on how it is defined, it is straightforward to show that it is a homeomorphism between  and
and  .
.
Claim 2
The 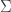 -product
-product 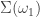 has the interesting property it is homeomorphic to its countable power, i.e.
has the interesting property it is homeomorphic to its countable power, i.e.
 .
.
Because each element of 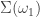 is nonzero only at countably many coordinates, concatenating countably many elements of
is nonzero only at countably many coordinates, concatenating countably many elements of 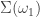 produces an element of
produces an element of 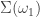 . Thus Claim 2 can be easily verified. With above claims, we can see that
. Thus Claim 2 can be easily verified. With above claims, we can see that
Thus  is a closed subspace of
is a closed subspace of 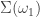 . Any closed subspace of a collectionwise normal space is collectionwise normal. We have established that
. Any closed subspace of a collectionwise normal space is collectionwise normal. We have established that  is normal.
is normal. 
____________________________________________________________________
The normality in the powers of 
We have established that 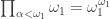 is not normal. Hence any higher uncountable power of
is not normal. Hence any higher uncountable power of  is not normal. We have also established that
is not normal. We have also established that  , the countable power of
, the countable power of  is normal (in fact collectionwise normal). Hence any finite power of
is normal (in fact collectionwise normal). Hence any finite power of  is normal. However
is normal. However  is not hereditarily normal. One of the exercises below is to show that
is not hereditarily normal. One of the exercises below is to show that  is not hereditarily normal.
is not hereditarily normal.
Theorem 2 can be generalized as follows:
Theorem 4
Let  be a countably compact space has an f.i.p. collection
be a countably compact space has an f.i.p. collection  of closed sets such that
of closed sets such that  . Then
. Then  is not normal where
is not normal where  .
.
The proof of Theorem 2 would go exactly like that of Theorem 2. Consider the following two theorems.
Theorem 5
Let  be a countably compact space that is not compact. Then there exists a cardinal number
be a countably compact space that is not compact. Then there exists a cardinal number  such that
such that  is not normal and
is not normal and 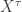 is normal for all cardinal number
is normal for all cardinal number  .
.
By the non-compactness of  , there exists an f.i.p. collection
, there exists an f.i.p. collection  of closed subsets of
of closed subsets of  such that
such that  . Let
. Let  be the least cardinality of such an f.i.p. collection. By Theorem 4, that
be the least cardinality of such an f.i.p. collection. By Theorem 4, that  is not normal. Because
is not normal. Because  is least, any smaller power of
is least, any smaller power of  must be normal.
must be normal.
Theorem 6
Let  be a space that is not countably compact. Then
be a space that is not countably compact. Then  is not normal for any cardinal number
is not normal for any cardinal number 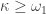 .
.
Since the space  in Theorem 6 is not countably compact, it would contain a closed and discrete subspace that is countable. By a theorem of A. H. Stone,
in Theorem 6 is not countably compact, it would contain a closed and discrete subspace that is countable. By a theorem of A. H. Stone,  is not normal. Then
is not normal. Then  is a closed subspace of
is a closed subspace of  .
.
Thus between Theorem 5 and Theorem 6, we can say that for any non-compact space  ,
,  is not normal for some cardinal number
is not normal for some cardinal number  . The
. The  from either Theorem 5 or Theorem 6 is at least
from either Theorem 5 or Theorem 6 is at least  . Interestingly for some spaces, the
. Interestingly for some spaces, the  can be much smaller. For example, for the Sorgenfrey line,
can be much smaller. For example, for the Sorgenfrey line,  . For some spaces (e.g. the Michael line),
. For some spaces (e.g. the Michael line),  .
.
Theorems 4, 5 and 6 are related to a theorem that is due to Noble.
Theorem 7 (Noble)
If each power of a space  is normal, then
is normal, then  is compact.
is compact.
A proof of Noble’s theorem is given in this earlier post, the proof of which is very similar to the proof of Theorem 2 given above. So the above discussion the normality of powers of  is just another way of discussing Theorem 7. According to Theorem 7, if
is just another way of discussing Theorem 7. According to Theorem 7, if  is not compact, some power of
is not compact, some power of  is not normal.
is not normal.
The material discussed in this post is excellent training ground for topology. Regarding powers of countably compact space and product of countably compact spaces, there are many topics for further discussion/investigation. One possibility is to examine normality in  for more examples of countably compact non-compact
for more examples of countably compact non-compact  . One particular interesting example would be a countably compact non-compact
. One particular interesting example would be a countably compact non-compact  such that the least power
such that the least power  for non-normality in
for non-normality in  is more than
is more than  . A possible candidate could be the second uncountable ordinal
. A possible candidate could be the second uncountable ordinal  . By Theorem 2,
. By Theorem 2,  is not normal. The issue is whether the
is not normal. The issue is whether the  power
power  and countable power
and countable power  are normal.
are normal.
____________________________________________________________________
Exercises
Exercise 1
Show that  is not hereditarily normal.
is not hereditarily normal.
Exercise 2
Show that the mapping  in Claim 3 in the proof of Theorem 3 is a homeomorphism.
in Claim 3 in the proof of Theorem 3 is a homeomorphism.
Exercise 3
The proof of Theorem 3 shows that the space  is a closed subspace of the
is a closed subspace of the 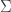 -product of the real line. Show that
-product of the real line. Show that  can be embedded in the
can be embedded in the 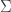 -product of arbitrary spaces.
-product of arbitrary spaces.
For each  , let
, let  be a space with at least two points. Let
be a space with at least two points. Let 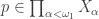 . The
. The 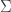 -product of the spaces
-product of the spaces  is the following subspace of the product space
is the following subspace of the product space 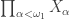 .
.
The point  is the center of the
is the center of the 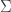 -product. Show that the space
-product. Show that the space 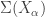 contains
contains  as a closed subspace.
as a closed subspace.
Exercise 4
Find a direct proof of Theorem 3, that  is normal.
is normal.
____________________________________________________________________
, which is the product of
with the interval topology (ordered topology) and the product space
where
is of course the unit interval
. The notation of
, the first uncountable ordinal, in Steen and Seebach is
.
is the product space
where
is
and
is the unit interval
for all
. Thus in this product space, all factors except for one factor is the unit interval and the lone non-compact factor is the first uncountable ordinal. The factor of
makes this product space an interesting example.
that are covered in [2] are:
is Hausdorff and completely regular.
is countably compact.
is neither compact nor sequentially compact.
is neither separable, Lindelof nor
-compact.
is not first countable.
is locally compact.
is not normal.
has a dense subspace that is normal.
is an example of a completely regular space that is not normal. Not being a normal space,
is then not metrizable. Of course there are other ways to show that
is not metrizable. One is that neither of the two factors
or
is metrizable. Another is that
is not first countable.
is not normal
is normal. The fact that it was not discussed in [2] could be that the tool for answering the normality question was not yet available at the time [2] was originally published, though we do not know for sure. It turns out that the tool became available in the paper [1] published a few years after the publication of [2]. The key to showing the normality (or the lack of) in the example
is to show whether the second factor
is a countably tight space.
, the product
is normal if and only if
is countably tight. For a proof of this theorem, see here. Thus the normality of the space
(or the lack of) hinges on whether the compact factor
is countably tight.
is countably tight (or has countable tightness) if for each
and for each
, there exists some countable
such that
. The definitions of tightness in general and countable tightness in particular are discussed here.
is not countably tight, we define
as follows. For each finite
, define
such that
maps
to 1 and maps
to 0. Let
be the set of
for all possible finite
. Let
be defined by
for all
.
. We claim that for any countable
,
. Let
be countable where each
is finite. Then choose
. Consider the open set
where
for
and
. Then
and
. Thus
. This shows that the product space
is not countably tight.
is not normal.
has a dense subspace that is normal
is not normal, a natural question is whether it has a dense subspace that is normal. Consider the subspace
where
is the
-product
where
is the space of all
such that for each
,
for at most countably many
.
is dense in the product space
. Thus
is dense in
. The space
is normal since the
-product of separable metric spaces is normal (see here). Furthermore,
can be embedded as a closed subspace of
. Then
is homeomorphic to a closed subspace of
. Note that
. Since
can be embedded as a closed subspace of the normal space
, the space
is normal.
2015 Dan Ma
