This is a discussion on a compact space called Helly space. The discussion here builds on the facts presented in Counterexample in Topology [2]. Helly space is Example 107 in [2]. The space is named after Eduard Helly.
Let be the closed unit interval with the usual topology. Let
be the set of all functions
. The set
is endowed with the product space topology. The usual product space notation is
or
where each
. As a product of compact spaces,
is compact.
Any function is said to be increasing if
for all
(such a function is usually referred to as non-decreasing). Helly space is the subspace
consisting of all increasing functions. This space is Example 107 in Counterexample in Topology [2]. The following facts are discussed in [2].
- The space
is compact.
- The space
is first countable (having a countable base at each point).
- The space
is separable.
- The space
has an uncountable discrete subspace.
From the last two facts, Helly space is a compact non-metrizable space. Any separable metric space would have countable spread (all discrete subspaces must be countable).
The compactness of stems from the fact that
is a closed subspace of the compact space
.
Further Discussion
Additional facts concerning Helly space are discussed.
- The product space
is normal.
- Helly space
contains a copy of the Sorgenfrey line.
- Helly space
is not hereditarily normal.
The space is the space of all countable ordinals with the order topology. Recall
is the product space
. The product space
is Example 106 in [2]. This product is not normal. The non-normality of
is based on this theorem: for any compact space
, the product
is normal if and only if the compact space
is countably tight. The compact product space
is not countably tight (discussed here). Thus
is not normal. However, the product
is normal since Helly space
is first countable.
To see that contains a copy of the Sorgenfrey line, consider the functions
defined as follows:
for all . Let
. Consider the mapping
defined by
. With the domain
having the Sorgenfrey topology and with the range
being a subspace of Helly space, it can be shown that
is a homeomorphism.
With the Sorgenfrey line embedded in
, the square
contains a copy of the Sorgenfrey plane
, which is non-normal (discussed here). Thus the square of Helly space is not hereditarily normal. A more interesting fact is that Helly space is not hereditarily normal. This is discussed in the next section.
Finding a Non-Normal Subspace of Helly Space
As before, is the product space
where
and
is Helly space consisting of all increasing functions in
. Consider the following two subspaces of
.
The subspace is a closed subset of
, hence compact. We claim that subspace
is separable and has a closed and discrete subset of cardinality continuum. This means that the subspace
is not a normal space.
First, we define a discrete subspace. For each with
, define
as follows:
Let . The set
as a subspace of
is discrete. Of course it is not discrete in
since
is compact. In fact, for any
,
(closure taken in
). However, it can be shown that
is closed and discrete as a subset of
.
We now construct a countable dense subset of . To this end, let
be a countable base for the usual topology on the unit interval
. For example, we can let
be the set of all open intervals with rational endpoints. Furthermore, let
be a countable dense subset of the open interval
(in the usual topology). For convenience, we enumerate the elements of
and
.
We also need the following collections.
For each and for each
with
, we would like to arrange the elements in increasing order, notated as follow:
For the set , we have
. For the set
,
is to the left of
for
. Note that elements of
are pairwise disjoint. Furthermore, write
. If
, then
. If
, then
.
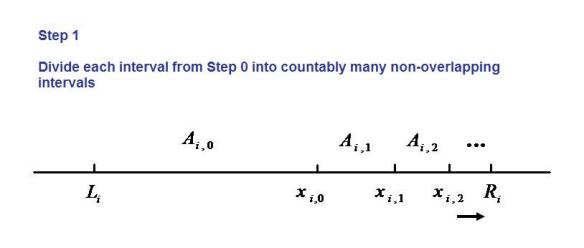
For each and
as detailed above, we define a function
as follows:
The following diagram illustrates the definition of when both
and
have 4 elements.
Let be the set of
over all
and
. The set
is a countable set. It can be shown that
is dense in the subspace
. In fact
is dense in the entire Helly space
.
To summarize, the subspace is separable and has a closed and discrete subset of cardinality continuum. This means that
is not normal. Hence Helly space
is not hereditarily normal. According to Jones’ lemma, in any normal separable space, the cardinality of any closed and discrete subspace must be less than continuum (discussed here).
Remarks
The preceding discussion shows that both Helly space and the square of Helly space are not hereditarily normal. This is actually not surprising. According to a theorem of Katetov, for any compact non-metrizable space , the cube
is not hereditarily normal (see Theorem 3 in this post). Thus a non-normal subspace is found in
,
or
. In fact, for any compact non-metric space
, an excellent exercise is to find where a non-normal subspace can be found. Is it in
, the square of
or the cube of
? In the case of Helly space
, a non-normal subspace can be found in
.
A natural question is: is there a compact non-metric space such that both
and
are hereditarily normal and
is not hereditarily normal? In other words, is there an example where the hereditarily normality fails at dimension 3? If we do not assume extra set-theoretic axioms beyond ZFC, any compact non-metric space
is likely to fail hereditarily normality in either
or
. See here for a discussion of this set-theoretic question.
Reference
- Kelly, J. L., General Topology, Springer-Verlag, New York, 1955.
- Steen, L. A., Seebach, J. A., Counterexamples in Topology, Dover Publications, Inc., New York, 1995.
Dan Ma topology
Daniel Ma topology
Dan Ma math
Daniel Ma mathematics
2019 – Dan Ma