In this post, we introduce a class of hyperspaces called Pixley-Roy spaces. This is a well-known and well studied set of topological spaces. Our goal here is not to be comprehensive but rather to present some selected basic results to give a sense of what Pixley-Roy spaces are like.
A hyperspace refers to a space in which the points are subsets of a given “ground” space. There are more than one way to define a hyperspace. Pixley-Roy spaces were first described by Carl Pixley and Prabir Roy in 1969 (see [5]). In such a space, the points are the non-empty finite subsets of a given ground space. More precisely, let  be a
be a  space (i.e. finite sets are closed). Let
space (i.e. finite sets are closed). Let ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) be the set of all non-empty finite subsets of
be the set of all non-empty finite subsets of  . For each
. For each ![F \in \mathcal{F}[X]](https://s0.wp.com/latex.php?latex=F+%5Cin+%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) and for each open subset
and for each open subset  of
of  with
with 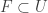 , we define:
, we define:
The sets ![[F,U]](https://s0.wp.com/latex.php?latex=%5BF%2CU%5D&bg=ffffff&fg=333333&s=0&c=20201002) over all possible
over all possible  and
and  form a base for a topology on
form a base for a topology on ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) . This topology is called the Pixley-Roy topology (or Pixley-Roy hyperspace topology). The set
. This topology is called the Pixley-Roy topology (or Pixley-Roy hyperspace topology). The set ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) with this topology is called a Pixley-Roy space.
with this topology is called a Pixley-Roy space.
The hyperspace as defined above was first defined by Pixley and Roy on the real line (see [5]) and was later generalized by van Douwen (see [7]). These spaces are easy to define and is useful for constructing various kinds of counterexamples. Pixley-Roy played an important part in answering the normal Moore space conjecture. Pixley-Roy spaces have also been studied in their own right. Over the years, many authors have investigated when the Pixley-Roy spaces are metrizable, normal, collectionwise Hausdorff, CCC and homogeneous. For a small sample of such investigations, see the references listed at the end of the post. Our goal here is not to discuss the results in these references. Instead, we discuss some basic properties of Pixley-Roy to solidify the definition as well as to give a sense of what these spaces are like. Good survey articles of Pixley-Roy are [3] and [7].
____________________________________________________________________
Basic Discussion
In this section, we focus on properties that are always possessed by a Pixley-Roy space given that the ground space is at least  . Let
. Let  be a
be a  space. We discuss the following points:
space. We discuss the following points:
- The topology defined above is a legitimate one, i.e., the sets
![[F,U]](https://s0.wp.com/latex.php?latex=%5BF%2CU%5D&bg=ffffff&fg=333333&s=0&c=20201002) indeed form a base for a topology on
indeed form a base for a topology on ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is a Hausdorff space.
is a Hausdorff space.![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is a zero-dimensional space.
is a zero-dimensional space.![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is a completely regular space.
is a completely regular space.![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is a hereditarily metacompact space.
is a hereditarily metacompact space.
Let ![\mathcal{B}=\left\{[F,U]: F \in \mathcal{F}[X] \text{ and } U \text{ is open in } X \right\}](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BB%7D%3D%5Cleft%5C%7B%5BF%2CU%5D%3A+F+%5Cin+%5Cmathcal%7BF%7D%5BX%5D+%5Ctext%7B+and+%7D+U+%5Ctext%7B+is+open+in+%7D+X+%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) . Note that every finite set
. Note that every finite set  belongs to at least one set in
belongs to at least one set in  , namely
, namely ![[F,X]](https://s0.wp.com/latex.php?latex=%5BF%2CX%5D&bg=ffffff&fg=333333&s=0&c=20201002) . So
. So  is a cover of
is a cover of ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) . For
. For ![A \in [F_1,U_1] \cap [F_2,U_2]](https://s0.wp.com/latex.php?latex=A+%5Cin+%5BF_1%2CU_1%5D+%5Ccap+%5BF_2%2CU_2%5D&bg=ffffff&fg=333333&s=0&c=20201002) , we have
, we have ![A \in [A,U_1 \cap U_2] \subset [F_1,U_1] \cap [F_2,U_2]](https://s0.wp.com/latex.php?latex=A+%5Cin+%5BA%2CU_1+%5Ccap+U_2%5D+%5Csubset+++%5BF_1%2CU_1%5D+%5Ccap+%5BF_2%2CU_2%5D&bg=ffffff&fg=333333&s=0&c=20201002) . So
. So  is indeed a base for a topology on
is indeed a base for a topology on ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
To show ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is Hausdorff, let
is Hausdorff, let  and
and  be finite subsets of
be finite subsets of  where
where  . Then one of the two sets has a point that is not in the other one. Assume we have
. Then one of the two sets has a point that is not in the other one. Assume we have 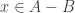 . Since
. Since  is
is  , we can find open sets
, we can find open sets 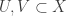 such that
such that 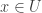 ,
,  and
and 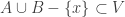 . Then
. Then ![[A,U \cup V]](https://s0.wp.com/latex.php?latex=%5BA%2CU+%5Ccup+V%5D&bg=ffffff&fg=333333&s=0&c=20201002) and
and ![[B,V]](https://s0.wp.com/latex.php?latex=%5BB%2CV%5D&bg=ffffff&fg=333333&s=0&c=20201002) are disjoint open sets containing
are disjoint open sets containing  and
and  respectively.
respectively.
To see that ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is a zero-dimensional space, we show that
is a zero-dimensional space, we show that  is a base consisting of closed and open sets. To see that
is a base consisting of closed and open sets. To see that ![[F,U]](https://s0.wp.com/latex.php?latex=%5BF%2CU%5D&bg=ffffff&fg=333333&s=0&c=20201002) is closed, let
is closed, let ![C \notin [F,U]](https://s0.wp.com/latex.php?latex=C+%5Cnotin+%5BF%2CU%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Either
. Either  or
or 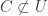 . In either case, we can choose open
. In either case, we can choose open 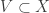 with
with 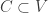 such that
such that ![[C,V] \cap [F,U]=\varnothing](https://s0.wp.com/latex.php?latex=%5BC%2CV%5D+%5Ccap+%5BF%2CU%5D%3D%5Cvarnothing&bg=ffffff&fg=333333&s=0&c=20201002) .
.
The fact that ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is completely regular follows from the fact that it is zero-dimensional.
is completely regular follows from the fact that it is zero-dimensional.
To show that ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is metacompact, let
is metacompact, let  be an open cover of
be an open cover of ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) . For each
. For each ![F \in \mathcal{F}[X]](https://s0.wp.com/latex.php?latex=F+%5Cin+%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) , choose
, choose 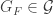 such that
such that  and let
and let ![V_F=[F,X] \cap G_F](https://s0.wp.com/latex.php?latex=V_F%3D%5BF%2CX%5D+%5Ccap+G_F&bg=ffffff&fg=333333&s=0&c=20201002) . Then
. Then ![\mathcal{V}=\left\{V_F: F \in \mathcal{F}[X] \right\}](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BV%7D%3D%5Cleft%5C%7BV_F%3A+F+%5Cin+%5Cmathcal%7BF%7D%5BX%5D+%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) is a point-finite open refinement of
is a point-finite open refinement of  . For each
. For each ![A \in \mathcal{F}[X]](https://s0.wp.com/latex.php?latex=A+%5Cin+%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) ,
,  can only possibly belong to
can only possibly belong to 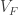 for the finitely many
for the finitely many 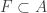 .
.
A similar argument show that ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is hereditarily metacompact. Let
is hereditarily metacompact. Let ![Y \subset \mathcal{F}[X]](https://s0.wp.com/latex.php?latex=Y+%5Csubset+%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Let
. Let 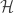 be an open cover of
be an open cover of  . For each
. For each 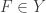 , choose
, choose 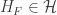 such that
such that 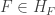 and let
and let ![W_F=([F,X] \cap Y) \cap H_F](https://s0.wp.com/latex.php?latex=W_F%3D%28%5BF%2CX%5D+%5Ccap+Y%29+%5Ccap+H_F&bg=ffffff&fg=333333&s=0&c=20201002) . Then
. Then 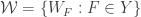 is a point-finite open refinement of
is a point-finite open refinement of 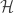 . For each
. For each 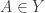 ,
,  can only possibly belong to
can only possibly belong to 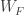 for the finitely many
for the finitely many 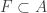 such that
such that 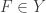 .
.
____________________________________________________________________
More Basic Results
We now discuss various basic topological properties of ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) . We first note that
. We first note that ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is a discrete space if and only if the ground space
is a discrete space if and only if the ground space  is discrete. Though we do not need to make this explicit, it makes sense to focus on non-discrete spaces
is discrete. Though we do not need to make this explicit, it makes sense to focus on non-discrete spaces  when we look at topological properties of
when we look at topological properties of ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) . We discuss the following points:
. We discuss the following points:
- If
 is uncountable, then
is uncountable, then ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is not separable.
is not separable.
- If
 is uncountable, then every uncountable subspace of
is uncountable, then every uncountable subspace of ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is not separable.
is not separable.
- If
![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is Lindelof, then
is Lindelof, then  is countable.
is countable.
- If
![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is Baire space, then
is Baire space, then  is discrete.
is discrete.
- If
![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) has the CCC, then
has the CCC, then  has the CCC.
has the CCC.
- If
![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) has the CCC, then
has the CCC, then  has no uncountable discrete subspaces,i.e.,
has no uncountable discrete subspaces,i.e.,  has countable spread, which of course implies CCC.
has countable spread, which of course implies CCC.
- If
![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) has the CCC, then
has the CCC, then  is hereditarily Lindelof.
is hereditarily Lindelof.
- If
![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) has the CCC, then
has the CCC, then  is hereditarily separable.
is hereditarily separable.
- If
 has a countable network, then
has a countable network, then ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) has the CCC.
has the CCC.
- The Pixley-Roy space of the Sorgenfrey line does not have the CCC.
- If
 is a first countable space, then
is a first countable space, then ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is a Moore space.
is a Moore space.
Bullet points 6 to 9 refer to properties that are never possessed by Pixley-Roy spaces except in trivial cases. Bullet points 6 to 8 indicate that ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) can never be separable and Lindelof as long as the ground space
can never be separable and Lindelof as long as the ground space  is uncountable. Note that
is uncountable. Note that ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is discrete if and only if
is discrete if and only if  is discrete. Bullet point 9 indicates that any non-discrete
is discrete. Bullet point 9 indicates that any non-discrete ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) can never be a Baire space. Bullet points 10 to 13 give some necessary conditions for
can never be a Baire space. Bullet points 10 to 13 give some necessary conditions for ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) to be CCC. Bullet 14 gives a sufficient condition for
to be CCC. Bullet 14 gives a sufficient condition for ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) to have the CCC. Bullet 15 indicates that the hereditary separability and the hereditary Lindelof property are not sufficient conditions for the CCC of Pixley-Roy space (though they are necessary conditions). Bullet 16 indicates that the first countability of the ground space is a strong condition, making
to have the CCC. Bullet 15 indicates that the hereditary separability and the hereditary Lindelof property are not sufficient conditions for the CCC of Pixley-Roy space (though they are necessary conditions). Bullet 16 indicates that the first countability of the ground space is a strong condition, making ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) a Moore space.
a Moore space.
__________________________________
To see bullet point 6, let  be an uncountable space. Let
be an uncountable space. Let 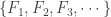 be any countable subset of
be any countable subset of ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Choose a point
. Choose a point 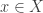 that is not in any
that is not in any 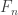 . Then none of the sets
. Then none of the sets  belongs to the basic open set
belongs to the basic open set ![[\left\{x \right\} ,X]](https://s0.wp.com/latex.php?latex=%5B%5Cleft%5C%7Bx+%5Cright%5C%7D+%2CX%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Thus
. Thus ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) can never be separable if
can never be separable if  is uncountable.
is uncountable.
__________________________________
To see bullet point 7, let ![Y \subset \mathcal{F}[X]](https://s0.wp.com/latex.php?latex=Y+%5Csubset+%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) be uncountable. Let
be uncountable. Let 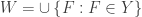 . Let
. Let 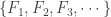 be any countable subset of
be any countable subset of  . We can choose a point
. We can choose a point 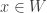 that is not in any
that is not in any 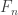 . Choose some
. Choose some 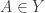 such that
such that 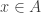 . Then none of the sets
. Then none of the sets 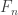 belongs to the open set
belongs to the open set ![[A ,X] \cap Y](https://s0.wp.com/latex.php?latex=%5BA+%2CX%5D+%5Ccap+Y&bg=ffffff&fg=333333&s=0&c=20201002) . So not only
. So not only ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is not separable, no uncountable subset of
is not separable, no uncountable subset of ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is separable if
is separable if  is uncountable.
is uncountable.
__________________________________
To see bullet point 8, note that ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) has no countable open cover consisting of basic open sets, assuming that
has no countable open cover consisting of basic open sets, assuming that  is uncountable. Consider the open collection
is uncountable. Consider the open collection ![\left\{[F_1,U_1],[F_2,U_2],[F_3,U_3],\cdots \right\}](https://s0.wp.com/latex.php?latex=%5Cleft%5C%7B%5BF_1%2CU_1%5D%2C%5BF_2%2CU_2%5D%2C%5BF_3%2CU_3%5D%2C%5Ccdots+%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) . Choose
. Choose 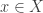 that is not in any of the sets
that is not in any of the sets 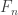 . Then
. Then 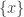 cannot belong to
cannot belong to ![[F_n,U_n]](https://s0.wp.com/latex.php?latex=%5BF_n%2CU_n%5D&bg=ffffff&fg=333333&s=0&c=20201002) for any
for any  . Thus
. Thus ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) can never be Lindelof if
can never be Lindelof if  is uncountable.
is uncountable.
__________________________________
For an elementary discussion on Baire spaces, see this previous post.
To see bullet point 9, let  be a non-discrete space. To show
be a non-discrete space. To show ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is not Baire, we produce an open subset that is of first category (i.e. the union of countably many closed nowhere dense sets). Let
is not Baire, we produce an open subset that is of first category (i.e. the union of countably many closed nowhere dense sets). Let 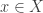 a limit point (i.e. an non-isolated point). We claim that the basic open set
a limit point (i.e. an non-isolated point). We claim that the basic open set ![V=[\left\{ x \right\},X]](https://s0.wp.com/latex.php?latex=V%3D%5B%5Cleft%5C%7B+x+%5Cright%5C%7D%2CX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is a desired open set. Note that
is a desired open set. Note that 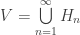 where
where
We show that each 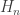 is closed and nowhere dense in the open subspace
is closed and nowhere dense in the open subspace  . To see that it is closed, let
. To see that it is closed, let 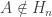 with
with 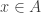 . We have
. We have 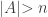 . Then
. Then ![[A,X]](https://s0.wp.com/latex.php?latex=%5BA%2CX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is open and every point of
is open and every point of ![[A,X]](https://s0.wp.com/latex.php?latex=%5BA%2CX%5D&bg=ffffff&fg=333333&s=0&c=20201002) has more than
has more than  points of the space
points of the space  . To see that
. To see that 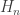 is nowhere dense in
is nowhere dense in  , let
, let ![[B,U]](https://s0.wp.com/latex.php?latex=%5BB%2CU%5D&bg=ffffff&fg=333333&s=0&c=20201002) be open with
be open with ![[B,U] \subset V](https://s0.wp.com/latex.php?latex=%5BB%2CU%5D+%5Csubset+V&bg=ffffff&fg=333333&s=0&c=20201002) . It is clear that
. It is clear that 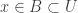 where
where  is open in the ground space
is open in the ground space  . Since the point
. Since the point  is not an isolated point in the space
is not an isolated point in the space  ,
,  contains infinitely many points of
contains infinitely many points of  . So choose an finite set
. So choose an finite set  with at least
with at least 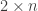 points such that
points such that  . For the the open set
. For the the open set ![[C,U]](https://s0.wp.com/latex.php?latex=%5BC%2CU%5D&bg=ffffff&fg=333333&s=0&c=20201002) , we have
, we have ![[C,U] \subset [B,U]](https://s0.wp.com/latex.php?latex=%5BC%2CU%5D+%5Csubset+%5BB%2CU%5D&bg=ffffff&fg=333333&s=0&c=20201002) and
and ![[C,U]](https://s0.wp.com/latex.php?latex=%5BC%2CU%5D&bg=ffffff&fg=333333&s=0&c=20201002) contains no point of
contains no point of 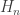 . With the open set
. With the open set  being a union of countably many closed and nowhere dense sets in
being a union of countably many closed and nowhere dense sets in  , the open set
, the open set  is not of second category. We complete the proof that
is not of second category. We complete the proof that ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is not a Baire space.
is not a Baire space.
__________________________________
To see bullet point 10, let 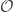 be an uncountable and pairwise disjoint collection of open subsets of
be an uncountable and pairwise disjoint collection of open subsets of  . For each
. For each 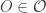 , choose a point
, choose a point 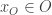 . Then
. Then ![\left\{[\left\{ x_O \right\},O]: O \in \mathcal{O} \right\}](https://s0.wp.com/latex.php?latex=%5Cleft%5C%7B%5B%5Cleft%5C%7B+x_O+%5Cright%5C%7D%2CO%5D%3A+O+%5Cin+%5Cmathcal%7BO%7D+%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) is an uncountable and pairwise disjoint collection of open subsets of
is an uncountable and pairwise disjoint collection of open subsets of ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Thus if
. Thus if ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is CCC then
is CCC then  must have the CCC.
must have the CCC.
__________________________________
To see bullet point 11, let 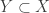 be uncountable such that
be uncountable such that  as a space is discrete. This means that for each
as a space is discrete. This means that for each 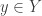 , there exists an open
, there exists an open 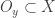 such that
such that 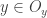 and
and 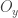 contains no point of
contains no point of  other than
other than  . Then
. Then ![\left\{[\left\{y \right\},O_y]: y \in Y \right\}](https://s0.wp.com/latex.php?latex=%5Cleft%5C%7B%5B%5Cleft%5C%7By+%5Cright%5C%7D%2CO_y%5D%3A+y+%5Cin+Y+%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) is an uncountable and pairwise disjoint collection of open subsets of
is an uncountable and pairwise disjoint collection of open subsets of ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Thus if
. Thus if ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) has the CCC, then the ground space
has the CCC, then the ground space  has no uncountable discrete subspace (such a space is said to have countable spread).
has no uncountable discrete subspace (such a space is said to have countable spread).
__________________________________
To see bullet point 12, let 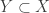 be uncountable such that
be uncountable such that  is not Lindelof. Then there exists an open cover
is not Lindelof. Then there exists an open cover  of
of  such that no countable subcollection of
such that no countable subcollection of  can cover
can cover  . We can assume that sets in
. We can assume that sets in  are open subsets of
are open subsets of  . Also by considering a subcollection of
. Also by considering a subcollection of  if necessary, we can assume that cardinality of
if necessary, we can assume that cardinality of  is
is 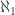 or
or  . Now by doing a transfinite induction we can choose the following sequence of points and the following sequence of open sets:
. Now by doing a transfinite induction we can choose the following sequence of points and the following sequence of open sets:
such that 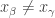 if
if 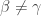 ,
, 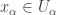 and
and 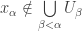 for each
for each  . At each step
. At each step  , all the previously chosen open sets cannot cover
, all the previously chosen open sets cannot cover  . So we can always choose another point
. So we can always choose another point 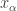 of
of  and then choose an open set in
and then choose an open set in  that contains
that contains 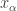 .
.
Then ![\left\{[\left\{x_\alpha \right\},U_\alpha]: \alpha < \omega_1 \right\}](https://s0.wp.com/latex.php?latex=%5Cleft%5C%7B%5B%5Cleft%5C%7Bx_%5Calpha+%5Cright%5C%7D%2CU_%5Calpha%5D%3A+%5Calpha+%3C+%5Comega_1+%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) is a pairwise disjoint collection of open subsets of
is a pairwise disjoint collection of open subsets of ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Thus if
. Thus if ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) has the CCC, then
has the CCC, then  must be hereditarily Lindelof.
must be hereditarily Lindelof.
__________________________________
To see bullet point 13, let 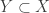 . Consider open sets
. Consider open sets ![[A,U]](https://s0.wp.com/latex.php?latex=%5BA%2CU%5D&bg=ffffff&fg=333333&s=0&c=20201002) where
where  ranges over all finite subsets of
ranges over all finite subsets of  and
and  ranges over all open subsets of
ranges over all open subsets of  with
with 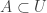 . Let
. Let  be a collection of such
be a collection of such ![[A,U]](https://s0.wp.com/latex.php?latex=%5BA%2CU%5D&bg=ffffff&fg=333333&s=0&c=20201002) such that
such that  is pairwise disjoint and
is pairwise disjoint and  is maximal (i.e. by adding one more open set, the collection will no longer be pairwise disjoint). We can apply a Zorn lemma argument to obtain such a maximal collection. Let
is maximal (i.e. by adding one more open set, the collection will no longer be pairwise disjoint). We can apply a Zorn lemma argument to obtain such a maximal collection. Let  be the following subset of
be the following subset of  .
.
We claim that the set  is dense in
is dense in  . Suppose that there is some open set
. Suppose that there is some open set 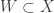 such that
such that 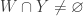 and
and 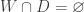 . Let
. Let 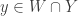 . Then
. Then ![[\left\{y \right\},W] \cap [A,U]=\varnothing](https://s0.wp.com/latex.php?latex=%5B%5Cleft%5C%7By+%5Cright%5C%7D%2CW%5D+%5Ccap+%5BA%2CU%5D%3D%5Cvarnothing&bg=ffffff&fg=333333&s=0&c=20201002) for all
for all ![[A,U] \in \mathcal{G}](https://s0.wp.com/latex.php?latex=%5BA%2CU%5D+%5Cin+%5Cmathcal%7BG%7D&bg=ffffff&fg=333333&s=0&c=20201002) . So adding
. So adding ![[\left\{y \right\},W]](https://s0.wp.com/latex.php?latex=%5B%5Cleft%5C%7By+%5Cright%5C%7D%2CW%5D&bg=ffffff&fg=333333&s=0&c=20201002) to
to  , we still get a pairwise disjoint collection of open sets, contradicting that
, we still get a pairwise disjoint collection of open sets, contradicting that  is maximal. So
is maximal. So  is dense in
is dense in  .
.
If ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) has the CCC, then
has the CCC, then  is countable and
is countable and  is a countable dense subset of
is a countable dense subset of  . Thus if
. Thus if ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) has the CCC, the ground space
has the CCC, the ground space  is hereditarily separable.
is hereditarily separable.
__________________________________
A collection 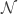 of subsets of a space
of subsets of a space  is said to be a network for the space
is said to be a network for the space  if any non-empty open subset of
if any non-empty open subset of  is the union of elements of
is the union of elements of 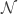 , equivalently, for each
, equivalently, for each 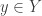 and for each open
and for each open 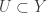 with
with 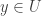 , there is some
, there is some 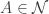 with
with 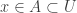 . Note that a network works like a base but the elements of a network do not have to be open. The concept of network and spaces with countable network are discussed in these previous posts Network Weight of Topological Spaces – I and Network Weight of Topological Spaces – II.
. Note that a network works like a base but the elements of a network do not have to be open. The concept of network and spaces with countable network are discussed in these previous posts Network Weight of Topological Spaces – I and Network Weight of Topological Spaces – II.
To see bullet point 14, let 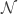 be a network for the ground space
be a network for the ground space  such that
such that 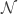 is also countable. Assume that
is also countable. Assume that 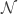 is closed under finite unions (for example, adding all the finite unions if necessary). Let
is closed under finite unions (for example, adding all the finite unions if necessary). Let ![\left\{[A_\alpha,U_\alpha]: \alpha < \omega_1 \right\}](https://s0.wp.com/latex.php?latex=%5Cleft%5C%7B%5BA_%5Calpha%2CU_%5Calpha%5D%3A+%5Calpha+%3C+%5Comega_1+%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) be a collection of basic open sets in
be a collection of basic open sets in ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Then for each
. Then for each  , find
, find 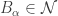 such that
such that 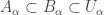 . Since
. Since 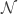 is countable, there is some
is countable, there is some 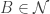 such that
such that 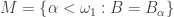 is uncountable. It follows that for any finite
is uncountable. It follows that for any finite 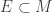 ,
, ![\bigcap \limits_{\alpha \in E} [A_\alpha,U_\alpha] \ne \varnothing](https://s0.wp.com/latex.php?latex=%5Cbigcap+%5Climits_%7B%5Calpha+%5Cin+E%7D+%5BA_%5Calpha%2CU_%5Calpha%5D+%5Cne+%5Cvarnothing&bg=ffffff&fg=333333&s=0&c=20201002) .
.
Thus if the ground space  has a countable network, then
has a countable network, then ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) has the CCC.
has the CCC.
__________________________________
The implications in bullet points 12 and 13 cannot be reversed. Hereditarily Lindelof property and hereditarily separability are not sufficient conditions for ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) to have the CCC. See [4] for a study of the CCC property of the Pixley-Roy spaces.
to have the CCC. See [4] for a study of the CCC property of the Pixley-Roy spaces.
To see bullet point 15, let  be the Sorgenfrey line, i.e. the real line
be the Sorgenfrey line, i.e. the real line  with the topology generated by the half closed intervals of the form
with the topology generated by the half closed intervals of the form 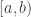 . For each
. For each 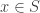 , let
, let 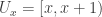 . Then
. Then ![\left\{[ \left\{ x \right\},U_x]: x \in S \right\}](https://s0.wp.com/latex.php?latex=%5Cleft%5C%7B%5B+%5Cleft%5C%7B+x+%5Cright%5C%7D%2CU_x%5D%3A+x+%5Cin+S+%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) is a collection of pairwise disjoint open sets in
is a collection of pairwise disjoint open sets in ![\mathcal{F}[S]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BS%5D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
__________________________________
A Moore space is a space with a development. For the definition, see this previous post.
To see bullet point 16, for each 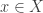 , let
, let 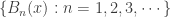 be a decreasing local base at
be a decreasing local base at  . We define a development for the space
. We define a development for the space ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
For each finite 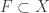 and for each
and for each  , let
, let  . Clearly, the sets
. Clearly, the sets 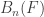 form a decreasing local base at the finite set
form a decreasing local base at the finite set  . For each
. For each  , let
, let 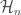 be the following collection:
be the following collection:
We claim that  is a development for
is a development for ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) . To this end, let
. To this end, let  be open in
be open in ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) with
with 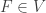 . If we make
. If we make  large enough, we have
large enough, we have ![[F,B_n(F)] \subset V](https://s0.wp.com/latex.php?latex=%5BF%2CB_n%28F%29%5D+%5Csubset+V&bg=ffffff&fg=333333&s=0&c=20201002) .
.
For each non-empty proper 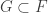 , choose an integer
, choose an integer 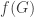 such that
such that ![[F,B_{f(G)}(F)] \subset V](https://s0.wp.com/latex.php?latex=%5BF%2CB_%7Bf%28G%29%7D%28F%29%5D+%5Csubset+V&bg=ffffff&fg=333333&s=0&c=20201002) and
and  . Let
. Let  be defined by:
be defined by:
We have  for all non-empty proper
for all non-empty proper 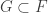 . Thus
. Thus ![F \notin [G,B_m(G)]](https://s0.wp.com/latex.php?latex=F+%5Cnotin+%5BG%2CB_m%28G%29%5D&bg=ffffff&fg=333333&s=0&c=20201002) for all non-empty proper
for all non-empty proper 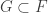 . But in
. But in 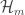 , the only sets that contain
, the only sets that contain  are
are ![[F,B_m(F)]](https://s0.wp.com/latex.php?latex=%5BF%2CB_m%28F%29%5D&bg=ffffff&fg=333333&s=0&c=20201002) and
and ![[G,B_m(G)]](https://s0.wp.com/latex.php?latex=%5BG%2CB_m%28G%29%5D&bg=ffffff&fg=333333&s=0&c=20201002) for all non-empty proper
for all non-empty proper 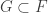 . So
. So ![[F,B_m(F)]](https://s0.wp.com/latex.php?latex=%5BF%2CB_m%28F%29%5D&bg=ffffff&fg=333333&s=0&c=20201002) is the only set in
is the only set in 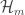 that contains
that contains  , and clearly
, and clearly ![[F,B_m(F)] \subset V](https://s0.wp.com/latex.php?latex=%5BF%2CB_m%28F%29%5D+%5Csubset+V&bg=ffffff&fg=333333&s=0&c=20201002) .
.
We have shown that for each open  in
in ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) with
with 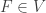 , there exists an
, there exists an  such that any open set in
such that any open set in 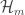 that contains
that contains  must be a subset of
must be a subset of  . This shows that the
. This shows that the 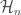 defined above form a development for
defined above form a development for ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
____________________________________________________________________
Examples
In the original construction of Pixley and Roy, the example was ![\mathcal{F}[\mathbb{R}]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5B%5Cmathbb%7BR%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Based on the above discussion,
. Based on the above discussion, ![\mathcal{F}[\mathbb{R}]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5B%5Cmathbb%7BR%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) is a non-separable CCC Moore space. Because the density (greater than
is a non-separable CCC Moore space. Because the density (greater than  for not separable) and the cellularity (
for not separable) and the cellularity (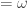 for CCC) do not agree,
for CCC) do not agree, ![\mathcal{F}[\mathbb{R}]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5B%5Cmathbb%7BR%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) is not metrizable. In fact, it does not even have a dense metrizable subspace. Note that countable subspaces of
is not metrizable. In fact, it does not even have a dense metrizable subspace. Note that countable subspaces of ![\mathcal{F}[\mathbb{R}]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5B%5Cmathbb%7BR%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) are metrizable but are not dense. Any uncountable dense subspace of
are metrizable but are not dense. Any uncountable dense subspace of ![\mathcal{F}[\mathbb{R}]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5B%5Cmathbb%7BR%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) is not separable but has the CCC. Not only
is not separable but has the CCC. Not only ![\mathcal{F}[\mathbb{R}]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5B%5Cmathbb%7BR%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) is not metrizable, it is not normal. The problem of finding
is not metrizable, it is not normal. The problem of finding 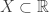 for which
for which ![\mathcal{F}[X]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) is normal requires extra set-theoretic axioms beyond ZFC (see [6]). In fact, Pixley-Roy spaces played a large role in the normal Moore space conjecture. Assuming some extra set theory beyond ZFC, there is a subset
is normal requires extra set-theoretic axioms beyond ZFC (see [6]). In fact, Pixley-Roy spaces played a large role in the normal Moore space conjecture. Assuming some extra set theory beyond ZFC, there is a subset 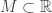 such that
such that ![\mathcal{F}[M]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5BM%5D&bg=ffffff&fg=333333&s=0&c=20201002) is a CCC metacompact normal Moore space that is not metrizable (see Example I in [8]).
is a CCC metacompact normal Moore space that is not metrizable (see Example I in [8]).
On the other hand, Pixley-Roy space of the Sorgenfrey line and the Pixley-Roy space of  (the first uncountable ordinal with the order topology) are metrizable (see [3]).
(the first uncountable ordinal with the order topology) are metrizable (see [3]).
The Sorgenfrey line and the first uncountable ordinal are classic examples of topological spaces that demonstrate that topological spaces in general are not as well behaved like metrizable spaces. Yet their Pixley-Roy spaces are nice. The real line and other separable metric spaces are nice spaces that behave well. Yet their Pixley-Roy spaces are very much unlike the ground spaces. This inverse relation between the ground space and the Pixley-Roy space was noted by van Douwen (see [3] and [7]) and is one reason that Pixley-Roy hyperspaces are a good source of counterexamples.
____________________________________________________________________
Reference
- Bennett, H. R., Fleissner, W. G., Lutzer, D. J., Metrizability of certain Pixley-Roy spaces, Fund. Math. 110, 51-61, 1980.
- Daniels, P, Pixley-Roy Spaces Over Subsets of the Reals, Topology Appl. 29, 93-106, 1988.
- Lutzer, D. J., Pixley-Roy topology, Topology Proc. 3, 139-158, 1978.
- Hajnal, A., Juahasz, I., When is a Pixley-Roy Hyperspace CCC?, Topology Appl. 13, 33-41, 1982.
- Pixley, C., Roy, P., Uncompletable Moore spaces, Proc. Auburn Univ. Conf. Auburn, AL, 1969.
- Przymusinski, T., Normality and paracompactness of Pixley-Roy hyperspaces, Fund. Math. 113, 291-297, 1981.
- van Douwen, E. K., The Pixley-Roy topology on spaces of subsets, Set-theoretic Topology, Academic Press, New York, 111-134, 1977.
- Tall, F. D., Normality versus Collectionwise Normality, Handbook of Set-Theoretic Topology (K. Kunen and J. E. Vaughan, eds), Elsevier Science Publishers B. V., Amsterdam, 685-732, 1984.
- Tanaka, H, Normality and hereditary countable paracompactness of Pixley-Roy hyperspaces, Fund. Math. 126, 201-208, 1986.
____________________________________________________________________

to gain insight about the function
. In this post, we draw more continuous functions with the goal of connecting
and
where
is the double arrow space. For example,
can be embedded as a subspace of
. More interestingly, both function spaces
and
share the same closed and discrete subspace of cardinality continuum. As a result, the function space
is not normal.
, which is a subset in the Euclidean plane.
with
, a basic open set containing the point
is of the form
, painted red in Figure 2. One the other hand, for any
with
, a basic open set containing the point
is of the form
, painted blue in Figure 2. The upper right point
and the lower left point
are made isolated points.
can be embedded as a subspace in the function
.
and
share the same closed and discrete subspace of cardinality continuum.
is not normal.
can be embedded into
, we draw a continuous map from the Sorgenfrey line
onto the double arrow space
. The following diagram gives the essential idea of the mapping we need.
onto the upper line segment of the double arrow space, as demonstrated by the red arrow. Thus
for any
with
. Essentially on the interval
, the mapping is the identity map.
onto the lower line segment of the double arrow space less the point
, as demonstrated by the blue arrow in Figure 3. Thus
for any
with
. Essentially on the interval
, the mapping is the identity map times -1.
in the domain. To complete the mapping, let
for any
and
for any
.
be the mapping that has been described. It maps the Sorgenfrey line onto the double arrow space. It is straightforward to verify that the map
is continuous.
can be embedded into
.
is a continuous image of the space
. Then
can be embedded into
.
can be embedded into
. The embedding that makes this true is
for each
. Thus each function
in
is identified with the composition
where
is the map defined in Figure 3. The fact that
is an embedding is shown in this previous post (see Theorem 1).
.
, let
be the continuous function described in Figure 4. The previous post shows that the set
is a closed and discrete subspace of
. We claim that
.
, we define continuous functions
such that
. We can actually back out the map
from
in Figure 4 and the mapping
. Here’s how. The function
is piecewise constant (0 or 1). Let’s focus on the interval
in the domain of
.
maps to the value 1. There are two intervals,
and
, where
maps to 1. The mapping
maps
to the set
. So the function
must map
to the value 1. The mapping
maps
to the set
. So
must map
to the value 1.
maps to the value 0. There are two intervals,
and
, where
maps to 0. The mapping
maps
to the set
. So the function
must map
to the value 0. The mapping
maps
to the set
. So
must map
to the value 0.
and
of the double arrow space, make sure that
maps these two points to the value 0. The following is a precise definition of the function
.
is a translation of
. Under the embedding
defined earlier, we see that
. Let
. The set
in
is homeomorphic to the set
in
. Thus
is a closed and discrete subspace of
since
is a closed and discrete subspace of
.
, the space of continuous functions on the double arrow space, contains a closed and discrete subspace of cardinality continuum. It follows that
is not normal. This is due to the fact that if
is normal, then
must have countable extent (i.e. all closed and discrete subspaces must be countable).
is embedded in
, the function space
is not embedded in
. Because the double arrow space is compact,
has countable tightness. If
were to be embedded in
, then
would be countably tight too. However,
is not countably tight due to the fact that
is not Lindelof (see Theorem 1 in this previous post).
-Theory Problem Book, Topological and Function Spaces, Springer, New York, 2011.
2018 – Dan Ma