Monthly Archives: September 2012

Stone-Cech Compactification is Maximal

Posted on by
Reply

Let X be a completely regular space. Let \beta X be the Stone-Cech compactification of X. In a previous post, we show that among all compactifcations of X, the Stone-Cech compactification \beta X is maximal with respect to a partial order \le (see Theorem C2 in Two Characterizations of Stone-Cech Compactification). As a result of the maximality, \beta X is the largest among all compactifications of X both in terms of cardinality and weight. We also establish an upper bound for the cardinality of \beta X and an upper bound for the weight of \beta X. As a result, we have upper bounds for cardinalities and weights for all compactifications of X. We prove the following points.

    Upper Bounds for Stone-Cech Compactification

  1. \lvert \beta X \lvert \le 2^{2^{d(X)}}.
  2. w(\beta X) \le 2^{d(X)}.

    3. Stone-Cech Compactification is Maximal

  3. For every compactification \alpha X of the space X, \lvert \alpha X \lvert \le \lvert \beta X \lvert.
  4. For every compactification \alpha X of the space X, w(\alpha X) \le w(\beta X).

    5. Upper Bounds for all Compactifications

  5. For every compactification \alpha X of the space X, w(\alpha X) \le 2^{d(X)}.
  6. For every compactification \alpha X of the space X, \lvert \alpha X \lvert \le 2^{2^{d(X)}}.

It is clear that Results 5 and 6 follow from the preceding results. The links for other posts on Stone-Cech compactification can be found toward the end of this post

___________________________________________________________________________________

Some Cardinal Functions

Let X be a space. The density of X is denoted by d(X) and is defined to be the smallest cardinality of a dense set in X. For example, if X is separable, then d(X)=\omega. The weight of the space X is denoted by w(X) and is defined to be the smallest cardinality of a base of the space X. For example, if X is second countable (i.e. having a countable space), then w(X)=\omega. Both d(X) and w(X) are cardinal functions that are commonly used in topological discussion. Most authors require that cardinal functions only take on infinite cardinals. We also adopt this convention here. We use c to denote the cardinality of the continuum (the cardinality of the real line \mathbb{R}).

If \mathcal{K} is a cardinal number, then 2^{\mathcal{K}} refers to the cardinal number that is the cardinallity of the set of all functions from \mathcal{K} to 2=\left\{0,1 \right\}. Equivalently, 2^{\mathcal{K}} is also the cardinality of the power set of \mathcal{K} (i.e. the set of all subsets of \mathcal{K}). If \mathcal{K}=\omega (the first infinite ordinal), then 2^\omega=c is the cardinality of the continuum.

If X is separable, then d(X)=\omega (as noted above) and we have 2^{d(X)}=c and 2^{2^{d(X)}}=2^c. Result 5 and Result 6 imply that 2^c is an upper bound for the cardinality of all compactifications of any separable space X and c is an upper bound of the weight of all compactifications of any separable space X.

In general, Result 5 and Result 6 indicate that the density of X bounds the cardinality of any compactification of X by two exponents and the density of X bounds the weight of any compactification of X by one exponent.

Another cardinal function related to weight is that of the network weight. A collection \mathcal{N} of subsets of the space X is said to be a network for X if for each point x \in X and for each open subset U of X with x \in U, there is some set A \in \mathcal{N} with x \in A \subset U. Note that sets in a network do not have to be open. However, any base for a topology is a network. The network weight of the space X is denoted by nw(X) and is defined to be the least cardinality of a network for X. Since any base is a network, we have nw(X) \le w(X). It is also clear that nw(X) \le \lvert X \lvert for any space X. Our interest in network and network weight is to facilitate the discussion of Lemma 2 below. It is a well known fact that in a compact space, the weight and the network weight are the same (see Result 5 in Spaces With Countable Network).
___________________________________________________________________________________

Some Basic Facts

We need the following two basic results.

    Lemma 1
    Let X be a space. Let C(X) be the set of all continuous functions f:X \rightarrow \mathbb{R}. Then \lvert C(X) \lvert \le 2^{d(X)}.

    Lemma 2
    Let S be a space and let T be a compact space. Suppose that T is the continuous image of S. Then w(T) \le w(S).

Proof of Lemma 1
Let A \subset X be a dense set with \lvert A \lvert=2^{d(X)}. Let \mathbb{R}^A be the set of all functions from A to \mathbb{R}. Consider the map W:C(X) \rightarrow \mathbb{R}^A by W(f)= f \upharpoonright A. This is a one-to-one map since f=g whenever f and g agree on a dense set. Thus we have \lvert C(X) \lvert \le \lvert \mathbb{R}^A \lvert. Upon doing some cardinal arithmetic, we have \lvert \mathbb{R}^A \lvert=2^{d(X)}. Thus Lemma 1 is established. \blacksquare

Proof of Lemma 2
Let g:S \rightarrow T be a continuous function from S onto T. Let \mathcal{B} be a base for S such that \lvert \mathcal{B} \lvert=w(S). Let \mathcal{N} be the set of all g(B) where B \in \mathcal{B}. Note that \mathcal{N} is a network for T (since g is a continuous function). So we have nw(T) \le \lvert \mathcal{N} \lvert \le \lvert \mathcal{B} \lvert = w(S). Since T is compact, w(T)=nw(T) (see Result 5 in Spaces With Countable Network). Thus we have nw(T)=w(T) \lvert \le w(S). \blacksquare

___________________________________________________________________________________

Results 1 and 2

Let X be a completely regular space. Let I be the unit interval [0,1]. We show that the Stone-Cech compactification \beta X can be regarded as a subspace of the product space I^{\mathcal{K}} where \mathcal{K}= 2^{d(X)} (the product of 2^{d(X)} many copies of I). The cardinality of I^{\mathcal{K}} is 2^{2^{d(X)}}, thus leading to Result 1.

Let C(X,I) be the set of all continuous functions f:X \rightarrow I. The Stone-Cech compactification \beta X is constructed by embedding X into the product space \prod \limits_{f \in C(X,I)} I_f where each I_f=I (see Embedding Completely Regular Spaces into a Cube or A Beginning Look at Stone-Cech Compactification). Thus \beta X is a subspace of I^{\mathcal{K}_1} where \mathcal{K}_1=\lvert C(X,I) \lvert.

Note that C(X,I) \subset C(X). Thus \beta X can be regarded as a subspace of I^{\mathcal{K}_2} where \mathcal{K}_2=\lvert C(X) \lvert. By Lemma 1, \beta X can be regarded as a subspace of the product space I^{\mathcal{K}} where \mathcal{K}= 2^{d(X)}.

To see Result 2, note that the weight of I^{\mathcal{K}} where \mathcal{K}= 2^{d(X)} is 2^{d(X)}. Then \beta X, as a subspace of the product space, must have weight \le 2^{d(X)}. \blacksquare

___________________________________________________________________________________

Results 3 and 4

What drives Result 3 and Result 4 is the following theorem (established in Two Characterizations of Stone-Cech Compactification).

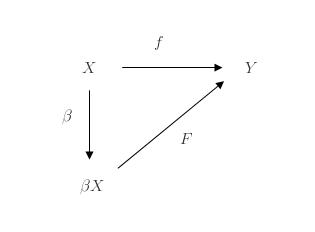
    Theorem C2
    Let X be a completely regular space. Among all compactifications of the space X, the Stone-Cech compactification \beta X of the space X is maximal with respect to the partial order \le.

    \text{ }

To define the partial order, for \alpha_1 X and \alpha_2 X, both compactifications of X, we say that \alpha_2 X \le \alpha_1 X if there is a continuous function f:\alpha_1 X \rightarrow \alpha_2 X such that f \circ \alpha_1=\alpha_2. See the following figure.

Figure 1

In this post, we use \le to denote this partial order as well as the order for cardinal numbers. Thus we need to rely on context to distinguish this partial order from the order for cardinal numbers.

Let \alpha X be a compactification of X. Theorem C2 indicates that \alpha X \le \beta X (partial order), which means that there is a continuous f:\beta X \rightarrow \alpha X such that f \circ \beta=\alpha (the same point in X is mapped to itself by f). Note that \alpha X is the image of \beta X under the function f:\beta X \rightarrow \alpha X. Thus we have \lvert \alpha X \lvert \le \lvert \beta X \lvert (cardinal number order). Thus Result 3 is established.

By Lemma 2, the existence of the continuous function f:\beta X \rightarrow \alpha X implies that w(\alpha X) \le w(\beta X) (cardinal number order). Thus Result 4 is established.

___________________________________________________________________________________

Blog Posts on Stone-Cech Compactification

___________________________________________________________________________________

Reference

  1. Engelking, R., General Topology, Revised and Completed edition, Heldermann Verlag, Berlin, 1989.
  2. Willard, S., General Topology, Addison-Wesley Publishing Company, 1970.

___________________________________________________________________________________

\copyright \ \ 2012

C*-Embedding Property and Stone-Cech Compactification

Posted on by
Reply

This is a continuation of an introduction of Stone-Cech compactification started in two previous posts (first post: A Beginning Look at Stone-Cech Compactification; second post: Two Characterizations of Stone-Cech Compactification). In this post, we present another characterization of the Stone-Cech compactification, that is, for any completely regular space X, X is C^*-embedded in its Stone-Cech compactification \beta X and that any compactification of X in which X is C^*-embedded must be \beta X. In other words, this property of C^*-embedding is unique to Stone-Cech compactification. We prove the following two theorems (U3 has two versions).

The links for other posts on Stone-Cech compactification can be found toward the end of this post.

___________________________________________________________________________________

    Definition. Let Y be a space. Let A \subset Y. The subspace A is C^*-embedded in Y if every bounded continuous function f:A \rightarrow \mathbb{R} is extendable to a continuous \hat{f}:Y \rightarrow \mathbb{R}.

    Theorem C3
    Let X be a completely regular space. The space X is C^*-embedded in its Stone-Cech compactification \beta X.

    \text{ }

    Theorem U3.1
    Let X be a completely regular space. Let I=[0,1]. Let \alpha X be a compactification of X such that each continuous f:X \rightarrow I can be extended to a continuous \hat{f}:\alpha X \rightarrow I. Then \alpha X must be \beta X.

    \text{ }

    Theorem U3.2
    If \alpha X is any compactification of X that satisfies the property in Theorem C3 (i.e., X is C^*-embedded in \alpha X), then \alpha X must be \beta X.
    \text{ }

___________________________________________________________________________________

Other Characterizations

Two other characterizations of \beta X are proved in the previous post (Two Characterizations of Stone-Cech Compactification).

    Theorem C1
    Let X be a completely regular space. Let f:X \rightarrow Y be a continuous function from X into a compact Hausdorff space Y. Then there is a continuous F: \beta X \rightarrow Y such that F \circ \beta=f.

    \text{ }

    Theorem U1
    If K is any compactification of X that satisfies condition in Theorem C1, then K must be equivalent to \beta X.
    \text{ }

    Theorem C2
    Let X be a completely regular space. Among all compactifications of the space X, the Stone-Cech compactification \beta X of the space X is the largest compactification.

    \text{ }

    Theorem U2
    The property in Theorem C2 is unique to \beta X. That is, if \alpha X is a compactification of X, then \alpha X must be equivalent to \beta X.

___________________________________________________________________________________

Remark

The C theorems and the U theorems are a great tool to determine whether a given compactification is \beta X. Whenever a compactification \alpha X of a space X satisfies the property belonging to a C theorem, based on the corresponding U theorem, we know that this compactification \alpha X must be \beta X. For example, any compactification \alpha X that satisfies the function extension property in Theorem C1 must be \beta X. Th C^*-embedding property in Theorem C3 and Theorem U3 (both versions) is also a function extension property much like that in Theorems C1 and U1, but is easier to use. The reason being that we only need to extend a smaller class of continuous functions (i.e., to check whether functions from X into I=[0,1] can be extended), rather than checking all continuous functions from X to arbitrary compact spaces. As the following example below about \beta \omega_1 illustrates that the C^*-embedding in Theorem C3 and U3.1 can be used to describe \beta X explicitly.

___________________________________________________________________________________

Proving Theorem U3.1 and Theorem U3.2

Let Y be a space. Let A be a subspace of X. Recall that A is C^*-embedded in Y if every bounded continuous function f:A \rightarrow \mathbb{R} can be extended to a continuous \hat{f}:Y \rightarrow \mathbb{R}.

Any bounded continuous function f: X \rightarrow \mathbb{R} can be regarded as f: X \rightarrow I_f where I_f is some closed and bounded interval. The C^*-embedding property in Theorem C3 is a function extension property like the one in Theorem C1, except that it deals with function from X into a specific type of compact spaces Y, namely the closed and bounded intervals in \mathbb{R}. Theorem C3 is a corollary of Theorem C1 (see below). So we only need to prove Theorem U3.1 and Theorem U3.2. Theorem U3.2 is a corollary of Theorem U3.1.

Proof of Theorem U3.1
By Theorem C2, we have \alpha X \le \beta X. So we only need to show \beta X \le \alpha X. To this end, we need to produce a continuous function H: \alpha X \rightarrow \beta X such that H \circ \alpha=\beta.

Let C(X,I) be the set of all continuous functions from X into I. For each f \in C(X,I), let I_f=I. Recall that \beta X is embedded in the cube \prod \limits_{f \in C(X,I)} I_f by the mapping \beta. For each f \in C(X,I), let \pi_f be the projection map from this cube into I_f.

Each f \in C(X,I) can be expressed as f=\pi_f \circ \beta. Thus by assumption, each f can be extended by \hat{f}: \alpha X \rightarrow I. Now define H: \alpha X \rightarrow \prod \limits_{f \in C(X,I)} I_f by the following:

    For each t \in \alpha X, H(t)=a=< a_f >_{f \in C(X,I)} such that a_f=\hat{f}(t)

For each x \in \alpha(X), we have H(\alpha(x))=\beta(x). Note that \hat{f} agrees with f on \alpha(X) since \hat{f} extends f. So we have H(\alpha(x))=a where a_f=\hat{f}(\alpha(x))=f(x) for each f \in C(X,I). On the other hand, by definition of \beta, we have \beta(x)=a where a_f=f(x) for each f \in C(X,I). Thus we have H \circ \alpha=\beta and the following:

    H(\alpha(X)) \subset \beta(X) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)

It is straightforward to verify that H is continuous. Note that \alpha(X) is dense in \alpha X. Since H is continuous, H(\alpha(X)) is dense in H(\alpha X). Thus we have:

    H(\alpha X)=\overline{H(\alpha(X))} \ \ \ \ \ \ \ \ \ \ \ \ \ (2)

Putting (1) and (2) together, we have the following:

    H(\alpha X)=\overline{H(\alpha(X))} \subset \overline{\beta(X)}=\beta X

Thus we can describe the map H as H: \alpha X \rightarrow \beta X. As noted before, we have H \circ \alpha=\beta. Thus \beta X \le \alpha X. \blacksquare

Proof of Theorem U3.2
Suppose \alpha X is a compactification of X such that X is C^*-embedded in \alpha X. Then every bounded continuous f:X \rightarrow I_f can be extended to \hat{f}:\alpha X \rightarrow I_f where I_f is some closed and bounded interval containing the range. In particular, this means every continuous f:X \rightarrow I can be extended. By Theorem U3.1, we have \alpha X \approx \beta X. \blacksquare

___________________________________________________________________________________

Example

This is one example where we can use C^*-embedding to describe \beta X explicitly.

Let \omega_1 be the first uncountable ordinal. Let \omega_1+1 be the successor ordinal of \omega_1 (i.e. \omega_1 with one additional point at the end). Consider X=\omega_1 and Y=\omega_1+1 as topological spaces with the order topology derived from the well ordering of the ordinals. The space Y is a compactification of X. In fact Y is the one-point compactification of X.

It is well known that every continuous real-valued function on X is bounded (note that X here is countably compact and hence pseudocompact). Furthermore, every continuous real-valued function on X is eventually constant. This means that if f:X \rightarrow \mathbb{R} is continuous, for some \alpha < \omega_1, f is constant on the final segment X_\alpha=\left\{\rho < \omega_1: \rho>\alpha \right\} (see result B in The First Uncountable Ordinal). As a result, every continuous bounded real-valued function f:X \rightarrow \mathbb{R} can be extended to a continuous \hat{f}:Y \rightarrow \mathbb{R}. Then according to Theorem U3.2, \beta X=\beta \omega_1=Y=\beta \omega_1+1.

___________________________________________________________________________________

Blog Posts on Stone-Cech Compactification

___________________________________________________________________________________

Reference

  1. Engelking, R., General Topology, Revised and Completed edition, Heldermann Verlag, Berlin, 1989.
  2. Willard, S., General Topology, Addison-Wesley Publishing Company, 1970.

___________________________________________________________________________________

\copyright \ \ 2012

Two Characterizations of Stone-Cech Compactification

Posted on by
Reply

This is the second post on Stone-Cech compactification (continuing from A Beginning Look at Stone-Cech Compactification). In this post, we establish two characterizations of Stone-Cech compactification. The first one is represented in the following diagram. The second one is that Stone-Cech compactification is maximal with respect to a certain partial order.

The first characterization is a central characteristic of Stone-Cech compactification. It is a function extension property that uniquely characterizes the Stone-Cech compactification of a completely regularly space. Here’s the diagram.

Figure 1

In this diagram, X is a completely regular space and \beta X is the Stone-Cech compactification of X where \beta is the homeomorphism mapping X onto \beta(X), which is dense in \beta X. The function f: X \rightarrow Y is an arbitrary continuous function where Y is compact. Then there exists a continuous function F:\beta X \rightarrow Y such that F restricted to \beta(X) is identical to the function f. In other words, if we think of X as a subset of \beta X, any continuous function from X to a compact space can be extended to all of \beta X. This function extension property is stated in Theorem C1 below.

    Theorem C1
    Let X be a completely regular space. Let f:X \rightarrow Y be a continuous function from X into a compact Hausdorff space Y. Then there is a continuous F: \beta X \rightarrow Y such that F \circ \beta=f. See Figure 1 above.
    \text{ }
    Theorem U1
    If K is any compactification of X that satisfies condition in Theorem C1, then K must be equivalent to \beta X.

Theorem C1 is the statement of the extension property described at the beginning. Theorem U1 states that this property is unique to \beta X. That is, of all the possible compactifications of X, only \beta X can satisfy Theorem C1.

For the other characterization, see Theorem C2 and Theorem U2 below.

_______________________________________________________________________________

Defining Stone-Cech Compactification

The definition of \beta X=\beta_X X is given in this previous post (A Beginning Look at Stone-Cech Compactification) and is repeated here again for the sake of completeness. Let C(X,I) be the set of all continuous functions from X into I=[0,1]. For each g \in C(X,I), I_g=[0,1]. The map \beta_X:X \rightarrow \prod \limits_{g \in C(X,I)} I_g is defined by:

    For each x \in X, \beta_X(x)=t=< t_g >_{g \in C(X,I)} is the point t \in \prod \limits_{g \in C(X,I)} I_g such that t_g=g(x) for each g \in C(X,I) (i.e. the g^{th} coordinate of the point t is g(x)).

For the proof that \beta_X is a homeomorphism, see A Beginning Look at Stone-Cech Compactification. We have the following definition.

    Definition
    Under the map \beta_X, \beta_X(X) is the topological copy of X within the cube \prod \limits_{f \in C(X,I)} I_f. The Stone-Cech compactification of X is defined to be the closure of \beta_X(X) in the cube \prod \limits_{f \in C(X,I)} I_f, i.e., set \beta_X X=\overline{\beta_X(X)}.

When there is no ambiguity as to what the space X is, the embedding \beta_X is written as \beta and the compactification \beta_X X is written as \beta X (as in Figure 1 above). When more than one space is involved, we use subscripts to distinguish the embeddings, e.g., \beta_X and \beta_Y.

_______________________________________________________________________________

Proof of Theorem U1

Let f:X \rightarrow Y be a continuous function from X into a compact Hausdorff space Y. Let \beta_X X be the Stone-Cech compactification of X where \beta_X is the homeomorphic embedding that defines \beta_X X. Since Y is a completely regular space, it has a Stone-Cech compactification \beta_Y Y, where \beta_Y is the homeomorphic embedding. We also define a map W from \prod \limits_{g \in C(X,I)} I_g into \prod \limits_{g \in C(Y,I)} I_k. We have the following diagram.

Figure 2

The desired function F will be defined by F=\beta_Y^{-1} \circ (W \upharpoonright \beta_X X). The rest of the proof is to define W and to show that this definition of F makes sense.

To define the function W, for each t \in \prod \limits_{g \in C(X,I)} I_g, let W(t)=a such that a_k=t_{k \circ f} (i.e. the k^{th} coordinate of W(t)=a is the (k \circ f)^{th} coordinate of t). With the definition of W, the diagram in Figure 2 commutes, i.e.,

    W \circ \beta_X=\beta_Y \circ f \ \ \ \ \ \ \ \ \ \ \ \ \ (1)

Starting with a point x \in X (the upper left corner of the diagram), we can reach the same point in the lower right corner regardless the path we take (W \circ \beta_X or \beta_Y \circ f). The following shows the derivation.

    One direction:
    x \in X

      \downarrow

    \beta_X(x)=t \text{ where } t_g=g(x) \ \forall \ g \in C(X,I)

      \downarrow

    W(t)=a \text{ where } a_k=t_{k \circ f}=(k \circ f)(x)=k(f(x)) \ \forall \ k \in C(Y,I)

    _________________________________
    The other direction:
    x \in X

      \downarrow

    f(x) \in Y

      \downarrow

    \beta_Y(f(x))=a \text{ where } a_k=k(f(x)) \ \forall \ k \in C(Y,I)

It is straightforward to verify that the map W is continuous. Based on (1) above, note that W(\beta_X(X)) \subset \beta_Y(Y). The following derivation shows that W(\beta_X X) \subset \beta_Y(Y).

    \displaystyle \begin{aligned} W(\beta_X X)&=W(\overline{\beta_X(X)}) \\&\subset \overline{W(\beta_X(X))} \ \ \ \ \text{ based on the continuity of } W\\&\subset \overline{\beta_Y(Y)} \ \ \ \ \ \ \ \ \ \ \text{ based on (1)}\\&=\beta_Y Y \\&=\beta_Y(Y) \ \ \ \ \ \ \ \ \ \ \text{ based on the compactness of Y} \end{aligned}

With the above derivation, we now know that the function W maps points of \beta_X X to points of \beta_Y(Y). So it makes sense to define F=\beta_Y^{-1} \circ (W \upharpoonright \beta_X X). Note that for each x \in X, we have:

    \displaystyle \begin{aligned} F(\beta_X(x))&=\beta_Y^{-1}(W(\beta_X(x)) \\&=\beta_Y^{-1}(\beta_Y(f(x))) \\&=f(x) \end{aligned}

Then we have F \circ \beta_X=f and F is the desired function. \blacksquare

_______________________________________________________________________________

Compactifications

In order to prove Theorem U1, we first have a basic discussion on compactifications. Most importantly, we pin down what we mean when we say two compactifications of X are equivalent. In the process, we produce another characterization of Stone-Cech compactification (see Theorem C2 and Theorem U2 below).

Let X be a completely regular space. A pair (T,\alpha) is said to be a compactification of the space X if T is a compact Hausdorff space and \alpha:X \rightarrow T is a homeomorphism from X into T such that \alpha(X) is dense in T. More informally, a compactification of the space X can also be thought of as a compact space T containing a topological copy of the space X as a dense subspace.

Given a compactification (T,\alpha), we use the notation \alpha X rather than the pair (T,\alpha). By saying that \alpha X is a compactification of X, we mean \alpha X is the compact space T where \alpha is the homeomorphism embedding X onto \alpha(X).

The Stone-Cech compactification construction above is an example of a compactification. There can be more than one compactification of a given space X. For example, for X=\mathbb{R}, we have the Stone-Cech compactification \beta \mathbb{R}, which is a subspace of the cube \prod \limits_{f \in C(\mathbb{R},I)} I_f. The circle S^1=\left\{(x,y) \in \mathbb{R}^2: x^2+y^2=1 \right\} contains a copy of the real line \mathbb{R} as a dense subspace, as does the unit interval [0,1]. Thus both S^1 and I=[0,1] are also compactifications of \mathbb{R}. See A Beginning Look at Stone-Cech Compactification for a discussion of these examples.

We say that compactifications \alpha_1 X and \alpha_2 X are equivalent (we write \alpha_1 X \approx \alpha_2 X) if there exists a homeomorphism f: \alpha_1 X \rightarrow \alpha_2 X such that f \circ \alpha_1= \alpha_2. In other words, the following diagram commutes.

Figure 3

Essentially, two compactifications \alpha_1 X and \alpha_2 X of X are equivalent if there is a homeomorphism f between the two and if each x \in X is mapped by f to itself, i.e., \alpha_1(x) is mapped to \alpha_2(x).

For a given completely regular space X, let \mathcal{C}(X) be the class of all compactifications of X. We define a partial order \le on \mathcal{C}(X). For \alpha_1 X and \alpha_2 X, both in \mathcal{C}(X), we say that \alpha_2 X \le \alpha_1 X if there is a continuous function f:\alpha_1 X \rightarrow \alpha_2 X such that f \circ \alpha_1=\alpha_2. See Figure 4 below.

Figure 4

The following theorem ties the partial order \le to the equivalence relation \approx for compactifications.

    Theorem 1
    Let \alpha_1 X and \alpha_2 X be two compactifications of X. Then \alpha_1 X \le \alpha_2 X and \alpha_2 X \le \alpha_1 X if and only if \alpha_1 X \approx \alpha_2 X.

Proof of Theorem 1
\Rightarrow With \alpha_2 X \le \alpha_1 X, there exists continuous f_1:\alpha_1 X \rightarrow \alpha_2 X such that

    f_1 \circ \alpha_1=\alpha_2 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (A1)

With \alpha_1 X \le \alpha_2 X, there exists continuous f_2:\alpha_2 X \rightarrow \alpha_1 X such that

    f_2 \circ \alpha_2=\alpha_1 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (A2)

Applying f_2 to (A1), we have f_2 \circ f_1 \circ \alpha_1=f_2 \circ \alpha_2. Applying (A2) to this result, we have

    f_2 \circ f_1 \circ \alpha_1=\alpha_1 \ \ \ \ \ \ \ \ \ \ \ (A3)

Note that f_2 \circ f_1 is a map from \alpha_1 X into \alpha_1 X. The equation (A3) indicates that when f_2 \circ f_1 is restricted to \alpha_1(X), it is the identity map. Thus f_2 \circ f_1 agrees with the identity map on the dense set \alpha_1(X). This implies that \alpha_1(X) must agree with the identity map on all of \alpha_1 X.

Likewise we can see that f_1 \circ f_2 must equal to the identity map on \alpha_2 X. So f_1:\alpha_1 X \rightarrow \alpha_2 X is a homeomorphism and it follows that \alpha_1 X and \alpha_2 X are equivalent compactifications of X.

\Leftarrow This direction is straightforward. Let f:\alpha_1 X \rightarrow \alpha_2 X a homeomorphism that makes \alpha_1 X and \alpha_2 X equivalent (as described by Figure 3). Then the map f implies \alpha_2 X \le \alpha_1 X and the map f^{-1} implies \alpha_1 X \le \alpha_2 X. \blacksquare

_______________________________________________________________________________

Another Characterization of the Stone-Cech Compactification

The next theorem says that the Stone-Cech compactification is the maximal compactification with respect to the partial order \le defined here. Furthermore, this property is unique (there is only one maximal compactification up to equivalence). This result will simplify the work when we need to show that a given compactification is equivalent to \beta X.

    Theorem C2
    Let X be a completely regular space. Among all compactifications of the space X, the Stone-Cech compactification \beta X of the space X is maximal with respect to the partial order \le.

    \text{ }

    Theorem U2
    The property in Theorem C2 is unique to \beta X. That is, if, among all compactifications of the space X, \alpha X is maximal with respect to the partial order \le, then \alpha X \approx \beta X.

Proof Theorem C2
Let \alpha X be any compactification of X. Consider the continuous map \alpha:X \rightarrow \alpha X. By Theorem C1, \alpha can be extended to \beta X. In other words, there exists a continuous F: \beta X \rightarrow \alpha X such that F \circ \beta = \alpha. The existence of the map F implies that \alpha X \le \beta X. \blacksquare

Proof Theorem U2
Let \alpha X be another maximal compactification of X. This implies that \beta X \le \alpha X. By Theorem C2, we have \alpha X \le \beta X. By Theorem 1, \alpha X must be equivalent to \beta X. \blacksquare

_______________________________________________________________________________

Proof of Theorem U1

We are now ready to prove Theorem U1.

Proof of Theorem U1
Let \alpha X be a compactification of X that satisfies the extension property in Theorem C1. In light of Theorem C2, we have \alpha X \le \beta X. So we only need to show \beta X \le \alpha X. Consider the map \beta: X \rightarrow \beta X. By the assumption that \alpha X satisfies the extension property in Theorem C1, there exists a continuous function F:\alpha X \rightarrow \beta X such that F \circ \alpha=\beta. The existence of F implies that \beta X \le \alpha X. By Theorem 1, \alpha X must be equivalent to \beta X. \blacksquare

_______________________________________________________________________________

Blog Posts on Stone-Cech Compactification

_______________________________________________________________________________

Reference

  1. Engelking, R., General Topology, Revised and Completed edition, Heldermann Verlag, Berlin, 1989.
  2. Willard, S., General Topology, Addison-Wesley Publishing Company, 1970.

_______________________________________________________________________________

\copyright \ \ 2012

A Beginning Look at Stone-Cech Compactification

Posted on by

For every completely regular space X, there exists a unique compact space \beta X containing X such that (1) \beta X has a dense subspace that is a topological copy of X and that (2) if X is considered as a subspace of \beta X, any continuous function f: X \rightarrow Y from X into a compact space Y can be extended to all of \beta X. The compact space \beta X is said to be the Stone-Cech compactification of X. We indicate how \beta X is constructed. The construction is done by embedding a completely regular space into a cube. To provide a glimpse of what \beta X might look like, we also take a brief look at \beta \mathbb{R}.

The links for other posts on Stone-Cech compactification can be found toward the end of this post.

_________________________________________________________________________

Construction

According to a theorem by Tychonoff from 1930, every completely regular space can be embedded in a cube. Embedding into a cube is one way Stone-Cech compactification is constructed. Let X be a completely regular space. Let I=[0,1] be the unit interval in the real line \mathbb{R}. Let C(X,I) be the set of all continuous real-valued functions defined on the space X. The cube for which X is embedded is I^{\mathcal{K}}, the product of \mathcal{K} copies of I where \mathcal{K} is the cardinality of C(X,I). We can also view I^{\mathcal{K}} as the product space \prod \limits_{f \in C(X,I)} I_f where each I_f=I. We can represent each point in the cube as a function t:C(X,I) \rightarrow I or as a sequence < t_f >_{f \in C(X,I)} such that each term (or coordinate) t_f \in I=[0,1].

The embedding from X into the cube \prod \limits_{f \in C(X,I)} I_f is the evaluation map \beta_X which is defined as: for each x \in X, \beta_X(x)=t=< t_f >_{f \in C(X,I)} is the point in the cube such that for each f \in C(X,I), t_f=f(x). This map \beta_X is shown to be a homeomorphism from X into \prod \limits_{f \in C(X,I)} I_f. What makes \beta_X a homeomorphism stems from the fact that in a completely regular space, there are enough bounded real-valued continuous functions to separate points from closed sets (see Embedding Completely Regular Spaces into a Cube). We have the following definition.

    Definition
    Under the map \beta_X, \beta_X(X) is the topological copy of X within the cube \prod \limits_{f \in C(X,I)} I_f. The Stone-Cech compactification of X is defined to be the closure of \beta_X(X) in the cube \prod \limits_{f \in C(X,I)} I_f, i.e., set \beta_X X=\overline{\beta_X(X)}.

According to the Tychonoff theorem, the cube \prod \limits_{f \in C(X,I)} I_f, being a product of compact spaces, is a compact space. Thus \beta_X X, being a closed subspace of the cube, is a compact space. Furthermore, \beta_X X contains a topological copy of X as a dense subspace.

When there is no ambiguity as to what the space X is, the embedding \beta_X is written as \beta and the compactification \beta_X X is written as \beta X.

_________________________________________________________________________

Characterization

Let X be a completely regular space. A compactification of X is a compact space K that has a dense subspace that is a topological copy of X. For a given X, there can be many compactifications of X. The Stone-Cech compactification \beta X has characteristics that are not shared by other compactifications of X. One such characteristic is stated at the beginning of the post and is repeated in the following two theorems.

    Theorem C1
    Let X be a completely regular space. Let f:X \rightarrow Y be a continuous function from X into a compact Hausdorff space Y. Then there is a continuous F: \beta X \rightarrow Y such that F \circ \beta=f. See Figure 1 below.
    \text{ }
    Theorem U1
    If K is any compactification of X that satisfies condition in Theorem C1, then K must be equivalent to \beta X.

Figure 1

When the continuous function F in Theorem C1 is restricted to to \beta(X), it is identical to the function f. If we think of X as a subset of \beta X, F extends f. Thus Theorem U1 essentially says that any continuous function from X into any compact space can be extended to all of \beta X. Theorem U1 says that the property stated in Theorem C1 uniquely characterizes \beta X. This means that any compactification of X that satisfies Theorem C1 must be equivalent to \beta X.

The proofs of Theorem C1 and Theorem U1 are found in the next post (Two Characterizations of Stone-Cech Compactification).

_________________________________________________________________________

Examples

We now look at \beta \mathbb{R}. We rely on Theorem C1 to provide some insight about \beta \mathbb{R}.

Note that S^1 and [0,1] are also compactifications of \mathbb{R}, where S^1 is the unit circle S^1=\left\{(x,y) \in \mathbb{R}^2: x^2+y^2=1 \right\}. First, we show the extension property described in Theorem C1 does not hold for both S^1 and [0,1]. Thus these two compactifications of \mathbb{R} cannot be \beta \mathbb{R}.

Consider the function \Phi(x):\mathbb{R} \rightarrow [0,1] defined by:

    \displaystyle \Phi(x)=\int_{-\infty}^x \ \frac{1}{\sqrt{2 \pi}} \ e^{\frac{- t^2}{2}} \ dt

Note that \Phi(x) is the cumulative distribution function (CDF) of the standard normal distribution. The following figure is the graph.

Figure 2

Note that S^1 is the one-point compactification of \mathbb{R}. Since \lim \limits_{x \rightarrow +\infty} \Phi(x)=1 and \lim \limits_{x \rightarrow -\infty} \Phi(x)=0, we cannot extend the function \Phi to a continuous function defined on S^1. Thus, S^1 as a compactification of \mathbb{R} cannot satisfy Theorem C1. It is clear that \beta \mathbb{R} cannot be S^1.

The closed unit interval [0,1] is the two-point compactification of \mathbb{R}. Now consider the function s(x)=sin(\frac{1}{x}) defined on the open interval (0,1), which is a topological copy of \mathbb{R}. It is impossible to extend s(x) to a continuous function defined on [0,1]. So to construct \beta \mathbb{R}, it take more than adding two additional points. In fact, the following discussion shows that \beta \mathbb{R} has uncountably many points in the remainder \beta \mathbb{R}-\mathbb{R}.

Consider the function the sine function w(x)=\text{sin}(x), which maps \mathbb{R} onto [-1,1]. Based on Theorem C1, w(x) can be extended to a function G: \beta \mathbb{R} \rightarrow [-1,1].

For each t \in [-1,1], let A_t=\left\{x \in \mathbb{R}: w(x)=\text{sin}(x)=t \right\}. For example, A_0 is the set \displaystyle \left\{n \pi: n=0, \pm 1, \pm 2, \pm 3, \cdots \right\}. Furthermore, for each t \in [-1,1], let B_t=G^{-1}(t), which is a compact set in \beta \mathbb{R}.

Consider \mathbb{R} as a subset of \beta \mathbb{R}. We have A_t \subset B_t for each t \in [-1,1]. Each A_t is a discrete set in \mathbb{R}. However, each A_t is not discrete in \beta \mathbb{R} (A_t is an infinite subset of a compact set in \beta \mathbb{R}). Thus B_t-A_t \ne \varnothing for each t \in [-1,1].

If we think of constructing a compactification as the process of adding points to X to form a compact space, the non-empty sets B_t-A_t show that at minimum we are adding continuum many points to form \beta \mathbb{R} (adding as many points as there are points in [-1,1] but in reality more than continuum many points are added). Note that for t \ne p, B_t and B_p are disjoint (they are separated by disjoint open sets in \beta \mathbb{R} through inverse images of the function G).

In fact, the cardinality of \beta \mathbb{R} is larger than continuum. Specifically, \lvert \beta \mathbb{R} \lvert=2^c, where c is the cardinality of \mathbb{R} and 2^c is the cardinality of the set of all subsets of \mathbb{R}. For this fact, see Corollary 3.6.12 in [1] or Exercise 19.H in [2].

The large size of \beta \mathbb{R} also tells us something about it topologically. It is a well known theorem in general topology that the cardinality of every first countable compact Hausdorff space is at most continuum (see Corollary 3.1.30 in [1] or see The cardinality of compact first countable spaces, I). Thus \beta \mathbb{R} cannot be first countable. The points at which it is not first countable are the points in the remainder \beta \mathbb{R}-\mathbb{R}. Not being a first countable, \beta \mathbb{R} is not metrizable.

Much more can be said about \beta \mathbb{R} and other Stone-Cech compactification \beta X. This brief walk in \beta \mathbb{R} shows that the Stone-Cech compactification can be quite large and quite different topologically even when the starting space is the familiar Euclidean space. In subsequent discussions, we will see that nice properties such as first countability, second countability and metrizability do not carry over from X to \beta X.

________________________________________________________________________

Blog Posts on Stone-Cech Compactification

________________________________________________________________________

Reference

  1. Engelking, R., General Topology, Revised and Completed edition, Heldermann Verlag, Berlin, 1989.
  2. Willard, S., General Topology, Addison-Wesley Publishing Company, 1970.

________________________________________________________________________

\copyright \ \ 2012

Sorgenfrey Line is not a Moore Space

Posted on by
Reply

We found an incorrect statement about the Sorgenfrey line in an entry in Wikipedia about Moore space (link). This statement opens up a discussion on the question of whether the Sorgenfrey line is a Moore space as well as a discussion on Moore space. The following is the incorrect statement found in Wikipedia by the author.

The Sorgenfrey line is the space whose underlying set is the real line S=\mathbb{R} where the topology is generated by a base consisting the half open intervals of the form [a,b). The Sorgenfrey plane is the square S \times S.

Even though the Sorgenfrey line is normal, the Sorgenfrey plane is not normal. In fact, the Sorgenfrey line is the classic example of a normal space whose square is not normal. Both the Sorgenfrey line and the Sorgenfrey plane are not Moore space but not for the reason given. The statement seems to suggest that any normal Moore space is second countable. But this flies in the face of all the profound mathematics surrounding the normal Moore space conjecture, which is also discussed in the Wikipedia entry.

The statement indicated above is only a lead-in to a discussion of Moore space. We are certain that it will be corrected. We always appreciate readers who kindly alert us to errors found in this blog.

______________________________________________________________________________

Moore Spaces

Let X be a regular space. A development for X is a sequence \mathcal{G}_1,\mathcal{G}_2,\mathcal{G}_3,\cdots of open covers of X such that for each x \in X, and for each open subset U of X with x \in U, there exists one cover \mathcal{G}_n satisfying the condition that for any open set V \in \mathcal{G}_n, x \in V \Rightarrow V \subset U. When X has a development, X is said to be a Moore space (also called developable space). A Note On The Sorgenfrey Line is an introductory note on the Sorgenfrey line.

Moore spaces can be viewed as a generalization of metrizable spaces. Moore spaces are first countable (having a countable base at each point). For a development \mathcal{G}_1,\mathcal{G}_2,\mathcal{G}_3,\cdots, the open sets in \mathcal{G}_n are considered “smaller” as the index n increases. In fact, this is how a development is defined for a metric space, where \mathcal{G}_n consists of all open balls with diameters less than \frac{1}{n}. Thus metric spaces are developable. There are plenty of non-metrizable Moore space. One example is the Niemytzki’s Tangent Disc space.

In a Moore space, every closed set is a G_\delta-set. Thus if a Moore space is normal, it is perfectly normal. Any Moore space has a G_\delta-diagonal (the diagonal \Delta=\left\{(x,x): x \in X \right\} is a G_\delta-set in X \times X). It is a well known theorem that every compact space with a G_\delta-diagonal is metrizable. Thus any compact Moore space is metrizable.

The last statement can be shown more directly. Suppose that X is compact and has a development \mathcal{G}_1,\mathcal{G}_2,\mathcal{G}_3,\cdots. Then each \mathcal{G}_n has a finite subcover \mathcal{H}_n. Then \bigcup_{n=1}^\infty \mathcal{H}_n is a countable base for X. Thus any compact Moore space is second countable and hence metrizable.

What about paracompact Moore space? Suppose that X is paracompact and has a development \mathcal{G}_1,\mathcal{G}_2,\mathcal{G}_3,\cdots. Then each \mathcal{G}_n has a locally finite open refinement \mathcal{H}_n. Then \bigcup_{n=1}^\infty \mathcal{H}_n is a \sigma-locally finite base for X. The Smirnov-Nagata metrization theorem states that a space is metrizable if and only if it has a \sigma-locally finite base (see Theorem 23.9 on page 170 of [2]). Thus any paracompact Moore space has a \sigma-locally finite base and is thus metrizable (after using the big gun of the Smirnov-Nagata metrization theorem).

______________________________________________________________________________

Sorgenfrey Line

The Sorgenfrey line is regular and Lindelof. Hence it is paracompact. Since the Sorgenfrey line is not metrizable, by the above discussion it cannot be a Moore space. The Sorgenfrey plane is also not a Moore space. Note that being a Moore space is a hereditary property. So if the Sorgenfrey plane is a Moore space, then every subspace of the Sorgenfrey plane (including the Sorgenfrey line) is a Moore space.

The following theorem is another way to show that the Sorgenfrey line is not a Moore space.

    Bing’s Metrization Theorem
    A topological space is metrizable if and only if it is a collectionwise normal Moore space.

Every paracompact space is collectionwise normal (see Theorem 5.1.18, p.305 of [1]). Thus the Sorgenfrey line is collectionwise normal and hence cannot be a Moore space. A space X is said to be collectionwise normal if X is a T_1-space and for every discrete collection \left\{W_\alpha: \alpha \in A \right\} of closed sets in X, there exists a discrete collection \left\{V_\alpha: \alpha \in A \right\} of open subsets of X such that W_\alpha \subset V_\alpha. For a proof of Bing’s metrization theorem, see page 329 of [1].

______________________________________________________________________________

Remark

The normal Moore space conjecture is the statement that every normal Moore space is metrizable. This conjecture had been one of the key motivating questions for many set theorists and topologists during a large part of the twentieth century. The bottom line is that this statement cannot not be decided just on the basis of the set of generally accepted axioms called Zermelo–Fraenkel set theory with the axiom of choice, commonly abbreviated ZFC. But Bing’s metrization theorem states that if we strengthen normality to collectionwise normality, we have a definite answer.

______________________________________________________________________________

Reference

  1. Engelking, R., General Topology, Revised and Completed edition, Heldermann Verlag, Berlin, 1989.
  2. Willard, S., General Topology, Addison-Wesley Publishing Company, 1970.

______________________________________________________________________________

\copyright \ \ 2012

An Example of a Completely Regular Space that is not Normal

Posted on by
Reply

We present an example of a space S that is Hausdorff, locally compact, zero-dimensional (having a base consisting of closed and open sets), metacompact, completely regular but not normal. This space S is a building block for defining other spaces. In a previous post, we show that the space S can be turned into a space that is regular but not completely regular by adding one point (see Regular but not Completely Regular). Even though S is discussed in the previous post, the space S is an interesting example by itself and deserves a separate post.

Let S be the set of all points (x,y) \in \mathbb{R} \times \mathbb{R} such that y \ge 0. For each real number x, define V_x to be the set V_x=\left\{(x,y) \in S: 0 \le y \le 2 \right\}, define D_x to be the set D_x=\left\{(s,s-x) \in S: x \le s \le x+2 \right\}, and define O_x=V_x \cup D_x. The topology on S is defined by the following:

  • Each point (x,y) \in S where y>0 is isolated.
  • For each point (x,0) \in S, a basic open set is of the form O_x - F where (x,0) \notin F and F is a finite subset of O_x.

It is straightforward to verify that the basic open sets defined above form a base for a topology on the set S and that the resulting topology is Hausdorff. One important observation to make is that this base consists of sets that are both closed and open. Whenever a space has a base consisting of closed and open sets, it is said to be a zero-dimensional space. It is straightforward to show that any zero-dimensional space is completely regular. Another interesting point about the space S is that it is metacompact. Recall that a space X is metacompact if every open cover of X has a point-finite open refinement.

Now we discuss why S is not normal. Note that the x-axis in S is a closed and discrete set of cardinality continuum. Jones’ lemma states that in a normal and separable space, the cardinality of any closed and discrete set must not equal to or exceed continuum. But Jones’ lemma is of no use here since S is not separable. However, the two disjoint closed sets that destroyed normality are from the x-axis, namely H=\left\{(x,0): x \in \mathbb{Q} \right\} and K=\left\{(x,0): x \in \mathbb{R}-\mathbb{Q} \right\}.

Note that H and K are disjoint closed sets in S. If S were normal, there would be a continuous f:S \rightarrow [0,1] such that f(a)=0 for all a \in H and f(a)=1 for all a \in K (using Urysohn lemma). But this function is not possible. It can be shown that any continuous function g:S \rightarrow [0,1] that maps H to zero would have to map the entire x-axis to zero except for a countable subset of x-axis. This fact follows from the Main Result presented in Regular but not Completely Regular.

________________________________________________________________________

Reference

  1. Engelking, R., General Topology, Revised and Completed edition, Heldermann Verlag, Berlin, 1989.
  2. Willard, S., General Topology, Addison-Wesley Publishing Company, 1970.

________________________________________________________________________

\copyright \ \ 2012

One way to get CCC spaces that are not separable

Posted on by
Reply

A space X is said to have countable chain condition (ccc) if every disjoint collection of open subsets of X is countable. For convenience, we refer to spaces that have countable chain condition as ccc spaces. It is easy to verify that separable spaces are ccc spaces. We present a specific way of generating spaces that always have ccc but are not separable. These spaces are the sigma products of separable spaces.

The product of separable spaces always have ccc (see Product of Spaces with Countable Chain Condition). However, the product of separable spaces is not separable when the number of factors is greater than continuum. Thus one way to get an example of ccc but not separable space is to take the product of more than continuum many separable spaces. For example, if c is the cardinality of continuum, \left\{0,1 \right\}^{2^c}, the product of 2^c many copies of \left\{0,1 \right\}, is a space that has ccc but is not separable.

________________________________________________________________________

Another example is obtained from taking sigma product of separable spaces. Let \left\{X_\alpha: \alpha \in A \right\} be a collection of spaces where A is some index set. Consider the product space \prod \limits_{\alpha \in A} X_\alpha. Fix a point p in the product. The sigma-product about the point p is denoted by \sum \limits_{\alpha \in A} X_\alpha and is the following subspace of the product space \prod \limits_{\alpha \in A} X_\alpha:

    \sum \limits_{\alpha \in A} X_\alpha=\left\{x \in \prod \limits_{\alpha \in A} X_\alpha: x(\alpha) \ne p(\alpha) \text{ for at most countably many } \alpha \right\}

To obtain the desired example, let A be an uncountable index set and let each X_\alpha be separable. The product space \prod \limits_{\alpha \in A} X_\alpha has ccc. Note that \sum \limits_{\alpha \in A} X_\alpha is always dense in the product space \prod \limits_{\alpha \in A} X_\alpha. Thus the sigma-product \sum \limits_{\alpha \in A} X_\alpha has ccc since it is a dense subspace of a ccc space. On the other hand, \sum \limits_{\alpha \in A} X_\alpha is never separable as long as there are uncountably many spaces X_\alpha.

As specific example, take X_\alpha=\left\{0,1 \right\} for each \alpha < \omega_1 and let the fixed point p be such that p(\alpha)=0 for all \alpha < \omega_1. The resulting \sum \limits_{\alpha < \omega_1} \left\{0,1 \right\} is a ccc space that is not separable. Of course, \sum \limits_{\alpha < \omega_1} X_\alpha in this case is the set of all x \in \left\{0,1 \right\}^{\omega_1} such that x(\alpha) \ne 0 for at most countably many \alpha < \omega_1.

One interesting note about the sigma-product \sum \limits_{\alpha < \omega_1} \left\{0,1 \right\} is that the overall product space \left\{0,1 \right\}^{\omega_1} is an example of a separable but not hereditarily separable space. Another interesting point is that \sum \limits_{\alpha < \omega_1} \left\{0,1 \right\} is a countably compact non-compact space (see A note about sigma-product of compact spaces).

________________________________________________________________________

Previous discussion of CCC spaces in this blog:

________________________________________________________________________

Reference

  1. Engelking, R., General Topology, Revised and Completed edition, Heldermann Verlag, Berlin, 1989.
  2. Willard, S., General Topology, Addison-Wesley Publishing Company, 1970.

________________________________________________________________________

\copyright \ \ 2012

Some basic properties of spaces with countable chain condition

Posted on by
Reply

A space X is said to have countable chain condition (ccc) if every disjoint collection of open subsets of X is countable. When a space has ccc, for convenience we also say that it is a ccc space. We present some basic results about ccc space as well as an equivalent condition for ccc in terms of relatively locally finite open collection. A corollary of this equivalent condition is that in the class of ccc spaces, paracompactness coincides with the Lindelof property.

____________________________________________________________________________

Basic Properties

Let X be a space. We have the following simple results about ccc spaces.

  1. If X is separable, then X has ccc.
  2. If X is hereditarily Lindelof, then X has ccc.
  3. The property ccc is hereditary with respect to open subspaces.
  4. Let Y be a dense subspace of X. Then Y has ccc if and only if X has ccc.

We only prove result 4.

Proof of 4
Let Y be a dense subspace of the space X. Suppose that X does not have ccc. Then there is an uncountable disjoint collection \mathcal{U} of open subsets of X. Assuming that Y is an uncountable set, the collection of all U \cap Y (where U \in \mathcal{U}) is an uncountable disjoint collection of open subsets of Y. It follows that Y does not have ccc. Thus Y has ccc implies X has ccc.

Suppose that Y does not have ccc. Then there is an uncountable disjoint collection \mathcal{V} of open subsets of Y. For each V \in \mathcal{V}, there is some V^*, open subset of X, such that V=V^* \cap Y. Let \mathcal{V}^* be the collection of all V^*. Note that \mathcal{V}^* is uncountable and is a disjoint collection of open subsets of X. It follows that X does not have ccc. Thus X has ccc implies Y has ccc. \blacksquare

Theorem 1 and Corollary 2 (stated below) are discussed in a previous post (Product of Spaces with Countable Chain Condition). Theorem 1 implies that if the ccc property is preserved by taking product of any finite number of factors, then the ccc property is preserved by taking product of any number of factors. As a corollary, it follows that the product of any number of separable spaces has ccc.

Theorem 1
Suppose that \left\{X_\alpha: \alpha \in T \right\} is a family of spaces such that \prod \limits_{\alpha \in F} X_\alpha has countable chain condition for every finite F \subset T. Then \prod \limits_{\alpha \in T} X_\alpha has countable chain condition.

Corollary 2
Suppose that \left\{X_\alpha: \alpha \in T \right\} is a family of separable spaces. Then \prod \limits_{\alpha \in T} X_\alpha has countable chain condition.

____________________________________________________________________________

An Equivalent Condition for Countable Chain Condition

The next theorem is an alternative way of looking at countable chain condition. Corollary 3 is an application of this equivalent condition.

Theorem 3
Let X be a space. Then the following conditions are equivalent.

  1. If \mathcal{U} is a collection of open subsets of X such that \mathcal{U} is locally countable in the open subspace \bigcup \mathcal{U}, then \mathcal{U} is countable.
  2. If \mathcal{U} is a collection of open subsets of X such that \mathcal{U} is locally finite in the open subspace \bigcup \mathcal{U}, then \mathcal{U} is countable.
  3. X has ccc.

Note that when an open collection \mathcal{U} is locally finite (locally countable) in the open subspace \bigcup \mathcal{U}, \mathcal{U} is said to be a relatively locally finite (locally countable) open collection.

Proof
The directions 1 \Rightarrow 2 and 2 \Rightarrow 3 are clear.

3 \Rightarrow 1
Suppose that X has ccc. Let \mathcal{U} be a collection of open subsets of X such that \mathcal{U} is locally countable in the open subspace \bigcup \mathcal{U}. For each U \in \mathcal{U}, choose a non-empty open set f(U) \subset U such that f(U) \cap O \ne \varnothing for at most countably many O \in \mathcal{U}. Let \mathcal{U}_f be the collection of all f(U) (over all U \in \mathcal{U}). Note that f is a countable-to-one mapping from \mathcal{U} into \mathcal{U}_f.

For H,K \in \mathcal{U}_f, a chain from H to K is any finite collection

    \left\{A_1,A_2,\cdots,A_n \right\} \subset \mathcal{U}_f

such that H=A_1, K=A_n, and for 1 \le j < n, A_j \cap A_{j+1} \ne \varnothing. For each V \in \mathcal{U}_f, let \mathcal{C}(V) be the following:

    \mathcal{C}(V)=\left\{W \in \mathcal{U}_f: \text{ there exists a chain from } V \text{ to } W \right\}

Note that every V \in \mathcal{U}_f meets only countably many sets in \mathcal{U}. Thus every V \in \mathcal{U}_f meets only countably many sets in \mathcal{U}_f. As a result, each \mathcal{C}(V) is countable. For each V \in \mathcal{U}_f, let \mathcal{E}(V)=\bigcup \mathcal{C}(V). For V_1,V_2 \in \mathcal{U}_f, if \mathcal{E}(V_1) \cap \mathcal{E}(V_2) \ne \varnothing, \mathcal{C}(V_1)=\mathcal{C}(V_2), and as a result \mathcal{E}(V_1)=\mathcal{E}(V_2). Thus the collection of all distinct \mathcal{E}(V) is a collection of disjoint open sets in X. Since X has ccc, there can be only countably many \mathcal{E}(V).

Each \mathcal{E}(V) is the union of countably many open sets, namely the open sets in \mathcal{C}(V), which is countable. Each set f(U) \in \mathcal{C}(V) is traced back to at most countably many sets in open sets U in the original collection \mathcal{U}. Since the mapping f is a countable-to-one map from \mathcal{U} to \mathcal{U}_f, \mathcal{U} is countable. \blacksquare

Corollary 4
Let X be a space with countable chain condition. Then X is a paracompact space if and only if X is a Lindelof space.

Proof
The direction \Leftarrow is the theorem that every regular Lindelof space is paracompact. See Theorem 3.8.11 and Theorem 5.1.2 in [1]. Also see Corollary 20.8 in [2].

\Rightarrow
This direction is a corollary of Theorem 3. Since X is paracompact, every open cover of the space X has a locally finite open refinement. By Theorem 3, the locally finite open refinement must be countable. \blacksquare

____________________________________________________________________________

Reference

  1. Engelking, R., General Topology, Revised and Completed edition, Heldermann Verlag, Berlin, 1989.
  2. Willard, S., General Topology, Addison-Wesley Publishing Company, 1970.

____________________________________________________________________________

\copyright \ \ 2012

Product of Spaces with Countable Chain Condition

Posted on by
Reply

A topological space is said to be separable if it has a countable dense subset. In any separable space, there cannot exist uncountably many pairwise disjoint open subsets (if that is the case, any dense set will have to be uncountable). A topological space X is said to have countable chain condition (ccc) if every disjoint collection of open subsets of X is countable. Thus any separable space is a space with ccc. We take a look at what happen when we take product of spaces with these two properties.

The product of two separable spaces is always a separable space. If A is a countable dense set in the space X and B is a countable dense set in the space Y, then A \times B is a countable dense set in the product space X \times Y. It follows that the product of finitely many separable spaces is separable. When the number of factors is infinite, the cardinality of the continuum is the dividing line. The product of separable spaces is sometimes separable (when the number of factors is less than or equal to continuum) and is sometimes not separable (when the number of factors is greater than continuum). For a discussion of this result, see Product of Separable Spaces in this blog, or see [1] and [3].

Is the product of two ccc spaces a space with ccc? It turns out that this question is independent of ZFC. That is, this question cannot be answered on the basis of the set of generally accepted axioms called Zermelo–Fraenkel set theory with the axiom of choice, commonly abbreviated ZFC (see [2], page 50). However it can be proven in ZFC that the product of any number of separable spaces has countable chain condition. In proving this result, Delta-system lemma is used.

___________________________________________________________________________

Delta-System Lemma

A collection \mathcal{D} of sets is said to be a Delta-system (or \Delta-system) if there is a set D such that for every A,B \in \mathcal{D} with A \ne B, we have A \cap B = D. When such set D exists, it is called the root of the Delta-system \mathcal{D}. The following is the statement of Delta-system lemma.

Lemma 1 – Delta-System Lemma
For every uncountable collection \mathcal{A} of finite sets, there is an uncountable \mathcal{D} \subset \mathcal{A} such that \mathcal{D} is a \Delta-system.

The statement of Delta-system lemma presented here is a special case (see [2], page 49) for the general version.

___________________________________________________________________________

Products of CCC Spaces

Even though the question of whether the product of two ccc spaces has ccc cannot be answered just within ZFC, we have a theorem that can gives us quite a bit of clarity. We have an amazing result that whenever the product of two ccc spaces has ccc, the product of any number of ccc spaces has ccc. Note that when countable chain condition is preserved by taking product with two factors, ccc is preserved by taking product with any finite number of factors. The following theorem shows that whenever ccc is preserved by taking product with any finite number of factors, ccc is preserved by taking the product of any number of factors. As a corollary, we have the result that the product of any number of separable spaces has ccc.

By manipulating the number of factors, we can easily obtain a space that has ccc but is not separable. For example, let \mathcal{K} be any cardinal that is larger than continuum. Then \left\{0,1\right\}^\mathcal{K} is a space that has ccc but is not separable.

Theorem 2
Suppose that \left\{X_\alpha: \alpha \in T \right\} is a family of spaces such that \prod \limits_{\alpha \in F} X_\alpha has countable chain condition for every finite F \subset T. Then \prod \limits_{\alpha \in T} X_\alpha has countable chain condition.

Proof
In proving the product space \prod \limits_{\alpha \in T} X_\alpha having ccc, it suffices to work with basic open sets of the form \prod \limits_{\alpha \in T} U_\alpha where U_\alpha=X_\alpha for all but finitely many \alpha \in T. Let \mathcal{U} be an uncountable collection of such basic open sets such that open sets in \mathcal{U} are pairwise disjoint.

For each G = \prod \limits_{\alpha \in T} U_\alpha \in \mathcal{U}, let A(G) be the finite set such that A(G) \subset T, and such that \alpha \in A(G) if and only if U_\alpha \ne X_\alpha. Let \mathcal{A} be the set of all such A(G). By Delta-system lemma, there is an uncountable \mathcal{D} \subset \mathcal{A} such that \mathcal{D} is a Delta-system. Let D be the root of this Delta-system.

The root of the Delta-system cannot be non-empty. If D = \varnothing, then for any A(G_1) \in \mathcal{D} and A(G_2) \in \mathcal{D} where A(G_1) \ne A(G_2) and G_1,G_2 \in \mathcal{U}, we have A(G_1) \cap A(G_2) = \varnothing, which leads to G_1 \cap G_2 \ne \varnothing. Thus D \ne \varnothing.

Let \mathcal{U}^* be the collection of all G \in \mathcal{U} such that A(G) \in \mathcal{D}. For each G = \prod \limits_{\alpha \in T} U_\alpha \in \mathcal{U}^*, let p(G)=\prod \limits_{\alpha \in D} U_\alpha (i.e. p is the projection map). Let \mathcal{U}^{**} be the collection of all p(G) where G \in \mathcal{U}^*.

We have the following observation:

  • Observation. For any A(G_1),A(G_2) \in \mathcal{D} with A(G_1) \ne A(G_2), \alpha \in A(G_1)-D implies \alpha \notin A(G_2)-D and \alpha \in A(G_2)-D implies \alpha \notin A(G_1)-D.

It follows from the above observation that the map p is a one-to-one map from \mathcal{U}^* into \mathcal{U}^{**}. Then \mathcal{U}^{**} is an uncountable collection of open subsets of \prod \limits_{\alpha \in D} X_\alpha, which has ccc by hypothesis. So there exists p(G_1),p(G_2) \in \mathcal{U}^{**} with p(G_1) \cap p(G_2) \ne \varnothing. The above observation allows us to define a point x \in G_1 \cap G_2, contradicting the assumption that \mathcal{U} is a pairwise disjoint collection. Thus the entire product space \prod \limits_{\alpha \in T} X_\alpha must have countable chain condition. \blacksquare

Corollary 3
Suppose that \left\{X_\alpha: \alpha \in T \right\} is a family of separable spaces. Then \prod \limits_{\alpha \in T} X_\alpha has countable chain condition.

Proof
This follows directly from Theorem 2. Note that the product of finitely many separable is separable (hence has ccc). \blacksquare

___________________________________________________________________________

Reference

  1. Engelking, R., General Topology, Revised and Completed edition, Heldermann Verlag, Berlin, 1989.
  2. Kunen, K., Set Theory, An Introduction to Independence Proofs, North-Holland, Amsterdam, 1980.
  3. Willard, S., General Topology, Addison-Wesley Publishing Company, 1970.

___________________________________________________________________________

\copyright \ 2012

Regular but not Completely Regular

Posted on by
Reply

Complete regularity is a separation axiom that is in between regularity and normality. In the previous posts we discuss some of the dominant roles played by complete regularity in the study of topology (see the three links below). In this post, we present an example of a regular space that is not completely regular. In such a space, all the construction techniques involving real-valued continuous maps discussed in these previous posts are not possible or are difficult to do. This example is another demonstration of the importance of completely regular spaces. Here’s the links to the previous posts.

A space X is said to be completely regular if X is a T_0 space and for each x \in X and for each closed subset A of X with x \notin A, there is a continuous function f:X \rightarrow [0,1] such that f(A) \subset \left\{0 \right\} and f(x)=1. Note that the T_0 axiom and the existence of the continuous function imply the T_1 axiom, which is equivalent to the property that single points are closed sets. Completely regular spaces are also called Tychonoff spaces.

Essentially, to show a space to be a completely regular space, it suffices to provide for a given closed set and a point (not in the closed set), a bounded real-valued continuous function that maps the given closed set and the point to two different real numbers a and b. So in a space that is not completely regular, there exist a closed set H and a point x \notin H such that every real-valued continuous function g that can be defined on the space maps H and the point x to the same real number.

The example of a regular but not completely regular space we define here is based on an elementary construction found in the literature (see [2] or Example 1.5.9 on page 40 of [1]). Other examples can also be found in the literature, e.g. the example called Deleted Tychonoff Corkscrew found in [3] (Example 91).

________________________________________________________________________

Defining the Example

We define a completely regular space S such that by adding a new point p the resulting space T=S \cup \left\{p \right\} is no longer completely regular. Let S be the set of all points (x,y) \in \mathbb{R} \times \mathbb{R} such that y \ge 0. Let p be a point not in S. For convenience we take p=(0,-1). The underlying set is T=S \cup \left\{p \right\}. The following figure illustrates the underlying set.

Figure 1 – Underlying Set

For each real number x, define V_x to be the set V_x=\left\{(x,y) \in S: 0 \le y \le 2 \right\}, define D_x to be the set D_x=\left\{(s,s-x) \in S: x \le s \le x+2 \right\}, and define O_x=V_x \cup D_x. The topology on T is defined by the following:

  • Each point (x,y) \in S where y>0 is isolated.
  • For each point (x,0) \in S, a basic open set is of the form O_x - F where (x,0) \notin F and F is a finite subset of O_x.
  • A basic open set at the point p is of the form \left\{p \right\} \cup U_n where n is a positive integer and U_n=\left\{(x,y) \in S: x \ge n \right\}.

The following figures illustrate the basic open sets at points (x,0) and at p.

Figure 2 – Basic Open Sets at the x-Axis

Figure 3 – Basic Open Sets at p

It is straightforward to verify that the basic open sets defined above form a base for a topology on the set T and that the resulting topology is Hausdorff. The space S is an interesting one that merits some attention. So we briefly discuss S before we show that the space T is regular but not completely regular.

________________________________________________________________________

Discussing the Space \bold S

One observation we like to make is that the basic open sets for points in S are both open and closed in S. Whenever a space has a base consisting of closed and open sets, it is said to be a zero-dimensional space. Because the members of one particular base are both closed and open, it follows that any zero-dimensional space is completely regular. As a zero-dimensional space, S is completely regular. In addition, S is locally compact. Note that the basic open sets defined above are compact.

However, the space S is not normal (shown in the last section below). Another point we would like to make is that S is metacompact (i.e. every open cover has a point-finite open refinement).

________________________________________________________________________

Main Result

We discuss a result that provides a lot of insight about the space S and the space T. For each integer n, let H_n=\left\{(x,0): n \le x \le n+1 \right\}=[n,n+1] \times \left\{0 \right\}. Let H=\left\{(x,0): x \in \mathbb{R} \right\} be the x-axis.

  • Main Result. Let n be an integer. If f:S \rightarrow \mathbb{R} be a continuous function such that f((x,0))=0 for infinitely many points (x,0) \in H_n, then for each integer j where j \ge n, f((x,0))=0 for all but countably many points (x,0) \in H_j.

We consider the following two claims.

Claim 1.
Let (a,0) \in H. If g:S \rightarrow \mathbb{R} is continuous and g((a,0))=0, then g(w)=0 for all but countably many points w \in O_a=V_a \cup D_a.

Claim 2.
Let (a,0) \in H. If g:S \rightarrow \mathbb{R} is continuous and g(w)=0 for countably infinitely many points w \in V_a -\left\{(a,0) \right\}, then g((a,0))=0.

Claim 1 follows from the way basic open sets are defined at the point (a,0) and the fact that g is a continuous function. Claim 2 also follows from the definition of open sets at (a,0).

We now prove the main result. Let A=\left\{(x(1),0),(x(2),0),(x(3),0),\cdots \right\} be a subset of H_n such that f((x(j),0))=0 for all j. For any point (a,b) \in S, let \pi((a,b))=a (the projection into the x-axis).

We first show that f(z)=0 for all but countably many z \in H_{n+1}. For each j \ge 1, let A_j be a countably infinite subset of D_{x(j)} such that f(w)=0 for all w \in D_{x(j)}-A_j. The sets A_j are possible by Claim 1. For each j, let B_j be the set of all \pi(w) where w \in A_j. Consider J=[n+1,n+2] - \bigcup_{j \ge 1} B_j. Note that J is the complement of a countable set. Let K=J \times \left\{0 \right\} which is a co-countable subset of H_{n+1}. For each (x,0) \in K, f(w)=0 for countably infinitely many w \in V_x (these points w are in V_x \cap (D_{x(j)}-A_j)). Thus by Claim 2, for each (x,0) \in K, f((x,0))=0.

Now that the f(b)=0 for infinitely many b \in H_{n+1}, we can continue the same argument to prove the same for the next interval H_{n+2}. Continue the same inductive process, we can show that for each integer k>1, f(z)=0 for all but countably many z \in H_{n+k}.

________________________________________________________________________

Discussing the Space \bold T

We now show that T is not completely regular. Let H_0=[0,1] \times \left\{0 \right\}, which is a closed set in T. Let f:T \rightarrow \mathbb{R} be continuous such that f(H_0) \subset \left\{0 \right\}. Then we show that f(p)=0. This follows from the main result. By the main result derived above, for each integer j \ge 1, f(w)=0 for all by countably many w \in H_j =[j,j+1] \times \left\{0 \right\}. Then f(p) has no choice by to be zero as well.

It remains to be shown that T is regular. Since the subspace S is completely regular, we only need to verify the regularity at the point p. Note that for the open set U_j, the closure is \overline{U_j}=U_j \cup H_{j-1} \cup H_{j-2}. Furthermore, \overline{U_j} \subset U_{j-2}. For each closed set C \subset T with x \notin C, choose some integer n such that p \in U_n \subset T-C. Then we have p \in U_{n+2} \subset \overline{U_{n+2}} \subset U_n \subset T-C. This establishes the regularity of T.

________________________________________________________________________

The Non-Normality of the Space \bold S

The main result derived above also shows that the space S is not normal. Let L be the set of all (x,0) where x \ge 0 and x is a rational number. Let M be the set of all (x,0) where x \ge 0 and x is an irrational number. Note that L and M are disjoint closed sets in S. If S is normal, then by the Urysohn lemma there is a continuous function \rho: S \rightarrow [0,1] such that \rho(L) \subset \left\{0 \right\} and \rho(M) \subset \left\{1 \right\}.

Such function \rho is not possible. To see this, suppose \rho exists. Note that \rho(w)=0 for infinitely many w \in H_0, namely all w=(x,0) where x \ge 0 is rational. By the main result, \rho(w)=0 for all but countably many w in the x-axis to the right of H_0. But \rho((x,0))=1 for all irrational x \ge 0.

________________________________________________________________________

Reference

  1. Engelking, R., General Topology, Revised and Completed edition, Heldermann Verlag, Berlin, 1989.
  2. Mysior, A., A Regular Space Which Is Not Completely Regular, Proc. Amer. Math. Soc., 81852-853, 1981.
  3. Steen, L. A., Seebach, J. A., Counterexamples in Topology, Dover Publications, Inc., New York, 1995.
  4. Willard, S., General Topology, Addison-Wesley Publishing Company, 1970.