Drawing Sorgenfrey continuous functions

Posted on September 5, 2017 by Dan Ma

The Sorgenfrey line is a well known topological space. It is the real number line with open intervals defined as sets of the form $[a,b)$ . Though this is a seemingly small tweak, it generates a vastly different space than the usual real number line. In this post, we look at the Sorgenfrey line from the continuous function perspective, in particular, the continuous functions that map the Sorgenfrey line into the real number line. In the process, we obtain insight into the space of continuous functions on the Sorgenfrey line.

The next post is a continuation on the theme of drawing Sorgenfrey continuous functions.

The Sorgenfrey Line

Let $\mathbb{R}$ denote the real number line. The usual open intervals are of the form $(a,b)=\left\{x \in \mathbb{R}: a<x<b \right\}$ . The union of such open intervals is called an open set. If more than one topologies are considered on the real line, these open sets are referred to as the usual open sets or Euclidean open sets (on the real line). The open intervals $(a,b)$ form a base for the usual topology on the real line. One important fact abut the usual open sets is that the usual open sets can be generated by the intervals $(a,b)$ where both end points are rational numbers. Thus the usual topology on the real line is said to have a countable base.

Now tweak the usual topology by calling sets of the form $[a,b)=\left\{x \in \mathbb{R}: a \le x<b \right\}$ open intervals. Then form open sets by taking unions of all such open intervals. The collection of such open sets is called the Sorgenfrey topology (on the real line). The real number line $\mathbb{R}$ with the Sorgenfry topology is called the Sorgenfrey line, denoted by $\mathbb{S}$ . The Sorgenfrey line has been discussed in this blog, starting with this post. This post examines continuous functions from $\mathbb{S}$ into the real line. In the process, we gain insight on the space of continuous functions defined on $\mathbb{S}$ .

Note that any usual open interval $(a,b)$ is the union of intervals of the form $[c,d)$ . Thus any usual (Euclidean) open set is an open set in the Sorgenfrey line. Thus the usual topology (on the real line) is contained in the Sorgenfrey topology, i.e. the usual topology is a weaker (coarser) topology.

Let $C(\mathbb{R})$ be the set of all continuous functions $f:\mathbb{R} \rightarrow \mathbb{R}$ where the domain is the real number line with the usual topology. Let $C(\mathbb{S})$ be the set of all continuous functions $f:\mathbb{S} \rightarrow \mathbb{R}$ where the domain is the Sorgenfrey line. In both cases, the range is always the number line with the usual topology. Based on the preceding paragraph, any continuous function $f:\mathbb{R} \rightarrow \mathbb{R}$ is also continuous with respect to the Sorgenfrey line, i.e. $C(\mathbb{R}) \subset C(\mathbb{S})$ .

Pictures of Continuous Functions

Consider the following two continuous functions.

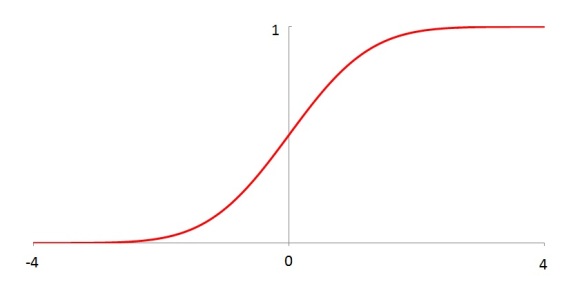
Figure 1 – CDF of the standard normal distribution

Figure 2 – CDF of the uniform distribution

The first one (Figure 1) is the cumulative distribution function (CDF) of the standard normal distribution. The second one (Figure 2) is the CDF of the uniform distribution on the interval $(0,a)$ where $a>0$ . Both of these are continuous in the usual Euclidean topology (in the domain). Such graphs would make regular appearance in a course on probability and statistics. They also show up in a calculus course as an everywhere differentiable curve (Figure 1) and as a differentiable curve except at finitely many points (Figure 2). Both of these functions can also be regarded as continuous functions on the Sorgenfrey line.

Consider a function that is continuous in the Sorgenfrey line but not continuous in the usual topology.

Figure 3 – Right continuous function

Figure 3 is a function that maps the interval $(-\infty,0)$ to -1 and maps the interval $[0,\infty)$ to 1. It is not continuous in the usual topology because of the jump at $x=0$ . But it is a continuous function when the domain is considered to be the Sorgenfrey line. Because of the open intervals being $[a,b)$ , continuous functions defined on the Sorgenfrey line are right continuous.

The cumulative distribution function of a discrete probability distribution is always right continuous, hence continuous in the Sorgenfrey line. Here’s an example.

Figure 4 – CDF of a discrete uniform distribution

Figure 4 is the CDF of the uniform distribution on the finite set $\left\{0,1,2,3,4 \right\}$ , where each point has probability 0.2. There is a jump of height 0.2 at each of the points from 0 to 4. Figure 3 and Figure 4 are step functions. As long as the left point of a step is solid and the right point is hollow, the step functions are continuous on the Sorgenfrey line.

The take away from the last four figures is that the real-valued continuous functions defined on the Sorgenfrey line are right continuous and that step functions (with the left point solid and the right point hollow) are Sorgenfrey continuous.

A Family of Sorgenfrey Continuous Functions

The four examples of continuous functions shown above are excellent examples to illustrate the Sorgenfrey topology. We now introduce a family of continuous functions $f_a:\mathbb{S} \rightarrow \mathbb{R}$ for $0<a<1$ . These continuous functions will lead to additional insight on the function space whose domain space is the Sorgenfrey line.

For any $0<a<1$ , the following gives the definition and the graph of the function $f_a$ .

$\displaystyle f_a(x) = \left\{ \begin{array}{ll} \displaystyle 0 &\ \ \ \ \ \ -\infty<x<-1 \\ \text{ } & \text{ } \\ \displaystyle 1 &\ \ \ \ \ \ -1 \le x<-a \\ \text{ } & \text{ } \\ 0 &\ \ \ \ \ \ -a \le x <a \\ \text{ } & \text{ } \\ 1 &\ \ \ \ \ \ a \le x <1 \\ \text{ } & \text{ } \\ 0 &\ \ \ \ \ \ 1 \le x <\infty \end{array} \right.$

Figure 5 – a family of Sorgenfrey continuous functions

Function Space on the Sorgenfrey Line

This is the place where we switch the focus to function space. The set $C(\mathbb{S})$ is a subset of the product space $\mathbb{R}^\mathbb{R}$ . So we can consider $C(\mathbb{S})$ as a topological space endowed with the topology inherited as a subspace of $\mathbb{R}^\mathbb{R}$ . This topology on $C(\mathbb{S})$ is called the pointwise convergence topology and $C(\mathbb{S})$ with the product subspace topology is denoted by $C_p(\mathbb{S})$ . See here for comments on how to work with the pointwise convergence topology.

For the present discussion, all we need is some notation on a base for $C_p(\mathbb{S})$ . For $x \in \mathbb{S}$ , and for any open interval $(a,b)$ (open in the usual topology of the real number line), let $[x,(a,b)]=\left\{h \in C_p(\mathbb{S}): h(x) \in (a, b) \right\}$ . Then the collection of intersections of finitely many $[x,(a,b)]$ would form a base for $C_p(\mathbb{S})$ .

The following is the main fact we wish to establish.

The function space $C_p(\mathbb{S})$ contains a closed and discrete subspace of cardinality continuum. In particular, the set $F=\left\{f_a: 0<a<1 \right\}$ is a closed and discrete subspace of $C_p(\mathbb{S})$ .

The above result will derive several facts on the function space $C_p(\mathbb{S})$ , which are discussed in a section below. More interestingly, the proof of the fact that $F=\left\{f_a: 0<a<1 \right\}$ is a closed and discrete subspace of $C_p(\mathbb{S})$ is based purely on the definition of the functions $f_a$ and the Sorgenfrey topology. The proof given below does not use any deep or high powered results from function space theory. So it should be a nice exercise on the Sorgenfrey topology.

I invite readers to either verify the fact independently of the proof given here or follow the proof closely. Lots of drawing of the functions $f_a$ on paper will be helpful in going over the proof. In this one instance at least, drawing continuous functions can help gain insight on function spaces.

Working out the Proof

The following diagram was helpful to me as I worked out the different cases in showing the discreteness of the family $F=\left\{f_a: 0<a<1 \right\}$ . The diagram is a valuable aid in convincing myself that a given case is correct.

Figure 6 – A comparison of three Sorgenfrey continuous functions

Now the proof. First, $F$ is relatively discrete in $C_p(\mathbb{S})$ . We show that for each $a$ , there is an open set $O$ containing $f_a$ such that $O$ does not contain $f_w$ for any $w \ne a$ . To this end, let $O=[a,V_1] \cap [-a,V_2]$ where $V_1$ and $V_2$ are the open intervals $V_1=(0.9,1.1)$ and $V_2=(-0.1,0.1)$ . With Figure 6 as an aid, it follows that for $0<b<a$ , $f_b \notin O$ and for $a<c<1$ , $f_c \notin O$ .

The open set $O=[a,V_1] \cap [-a,V_2]$ contains $f_a$ , the function in the middle of Figure 6. Note that for $0<b<a$ , $f_b(-a)=1$ and $f_b(-a) \notin V_2$ . Thus $f_b \notin O$ . On the other hand, for $a<c<1$ , $f_c(a)=0$ and $f_c(a) \notin V_1$ . Thus $f_c \notin O$ . This proves that the set $F$ is a discrete subspace of $C_p(\mathbb{S})$ relative to $F$ itself.

Now we show that $F$ is closed in $C_p(\mathbb{S})$ . To this end, we show that

$g \in C_p(\mathbb{S})$

$U$

$g$

$U$

$F$

Actually, this has already been done above with points $g$ that are in $F$ . One thing to point out is that the range of $f_a$ is $\left\{0,1 \right\}$ . As we consider $g \in C_p(\mathbb{S})$ , we only need to consider $g$ that maps into $\left\{0,1 \right\}$ . Let $g \in C_p(\mathbb{S})$ . The argument is given in two cases regarding the function $g$ .

Case 1. There exists some $a \in (0,1)$ such that $g(a) \ne g(-a)$ .

We assume that $g(a)=0$ and $g(-a)=1$ . Then for all $0<b<a$ , $f_b(a)=1$ and for all $a<c<1$ , $f_c(-a)=0$ . Let $U=[a,(-0.1,0.1)] \cap [-a,(0.9,1.1)]$ . Then $g \in U$ and $U$ contains no $f_b$ for any $0<b<a$ and $f_c$ for any $a<c<1$ . To help see this argument, use Figure 6 as a guide. The case that $g(a)=1$ and $g(-a)=0$ has a similar argument.

Case 2. For every $a \in (0,1)$ , we have $g(a) = g(-a)$ .

Claim. The function $g$ is constant on the interval $(-1,1)$ . Suppose not. Let $0<b<a<1$ such that $g(a) \ne g(b)$ . Suppose that $0=g(b) < g(a)=1$ . Consider $W=\left\{w<a: g(w)=0 \right\}$ . Clearly the number $a$ is an upper bound of $W$ . Let $u \le a$ be a least upper bound of $W$ . The function $g$ has value 1 on the interval $(u,a)$ . Otherwise, $u$ would not be the least upper bound of the set $W$ . There is a sequence of points $\left\{x_n \right\}$ in the interval $(b,u)$ such that $x_n \rightarrow u$ from the left such that $g(x_n)=0$ for all $n$ . Otherwise, $u$ would not be the least upper bound of the set $W$ .

It follows that $g(u)=1$ . Otherwise, the function $g$ is not continuous at $u$ . Now consider the 6 points $-a<-u<-b<b<u<a$ . By the assumption in Case 2, $g(u)=g(-u)=1$ and $g(b)=g(-b)=0$ . Since $g(x_n)=0$ for all $n$ , $g(-x_n)=0$ for all $n$ . Note that $-x_n \rightarrow -u$ from the right. Since $g$ is right continuous, $g(-u)=0$ , contradicting $g(-u)=1$ . Thus we cannot have $0=g(b) < g(a)=1$ .

Now suppose we have $1=g(b) > g(a)=0$ where $0<b<a<1$ . Consider $W=\left\{w<a: g(w)=1 \right\}$ . Clearly $W$ has an upper bound, namely the number $a$ . Let $u \le a$ be a least upper bound of $W$ . The function $g$ has value 0 on the interval $(u,a)$ . Otherwise, $u$ would not be the least upper bound of the set $W$ . There is a sequence of points $\left\{x_n \right\}$ in the interval $(b,u)$ such that $x_n \rightarrow u$ from the left such that $g(x_n)=1$ for all $n$ . Otherwise, $u$ would not be the least upper bound of the set $W$ .

It follows that $g(u)=0$ . Otherwise, the function $g$ is not continuous at $u$ . Now consider the 6 points $-a<-u<-b<b<u<a$ . By the assumption in Case 2, $g(u)=g(-u)=0$ and $g(b)=g(-b)=1$ . Since $g(x_n)=1$ for all $n$ , $g(-x_n)=1$ for all $n$ . Note that $-x_n \rightarrow -u$ from the right. Since $g$ is right continuous, $g(-u)=1$ , contradicting $g(-u)=0$ . Thus we cannot have $1=g(b) > g(a)=0$ .

The claim that the function $g$ is constant on the interval $(-1,1)$ is established. To wrap up, first assume that the function $g$ is 1 on the interval $(-1,1)$ . Let $U=[0,(0.9,1.1)]$ . It is clear that $g \in U$ . It is also clear from Figure 5 that $U$ contains no $f_a$ . Now assume that the function $g$ is 0 on the interval $(-1,1)$ . Since $g$ is Sorgenfrey continuous, it follows that $g(-1)=0$ . Let $U=[-1,(-0.1,0.1)]$ . It is clear that $g \in U$ . It is also clear from Figure 5 that $U$ contains no $f_a$ .

We have established that the set $F=\left\{f_a: 0<a<1 \right\}$ is a closed and discrete subspace of $C_p(\mathbb{S})$ .

What does it Mean?

The above argument shows that the set $F$ is a closed an discrete subspace of the function space $C_p(\mathbb{S})$ . We have the following three facts.

Three Results

$C_p(\mathbb{S})$ is separable.
$C_p(\mathbb{S})$ is not hereditarily separable.
$C_p(\mathbb{S})$ is not a normal space.

To show that $C_p(\mathbb{S})$ is separable, let’s look at one basic helpful fact on $C_p(X)$ . If $X$ is a separable metric space, e.g. $X=\mathbb{R}$ , then $C_p(X)$ has quite a few nice properties (discussed here). One is that $C_p(X)$ is hereditarily separable. Thus $C_p(\mathbb{R})$ , the space of real-valued continuous functions defined on the number line with the pointwise convergence topology, is hereditarily separable and thus separable. Recall that continuous functions in $C_p(\mathbb{R})$ are also Soregenfrey line continuous. Thus $C_p(\mathbb{R})$ is a subspace of $C_p(\mathbb{S})$ . The space $C_p(\mathbb{R})$ is also a dense subspace of $C_p(\mathbb{S})$ . Thus the space $C_p(\mathbb{S})$ contains a dense separable subspace. It means that $C_p(\mathbb{S})$ is separable.

Secondly, $C_p(\mathbb{S})$ is not hereditarily separable since the subspace $F=\left\{f_a: 0<a<1 \right\}$ is a closed and discrete subspace.

Thirdly, $C_p(\mathbb{S})$ is not a normal space. According to Jones’ lemma, any separable space with a closed and discrete subspace of cardinality of continuum is not a normal space (see Corollary 1 here). The subspace $F=\left\{f_a: 0<a<1 \right\}$ is a closed and discrete subspace of the separable space $C_p(\mathbb{S})$ . Thus $C_p(\mathbb{S})$ is not normal.

Remarks

The topology of the Sorgenfrey line is vastly different from the usual topology on the real line even though the the Sorgenfrey topology is obtained by a seemingly small tweak from the usual topology. The real line is a metric space while the Sorgenfrey line is not metrizable. The real number line is connected while the Sorgenfrey line is not. The countable power of the real number line is a metric space and thus a normal space. On the other hand, the Sorgenfrey line is a classic example of a normal space whose square is not normal. See here for a basic discussion of the Sorgenfrey line.

The pictures of Sorgenfrey continuous functions demonstrated here show that the real number line and the Sorgenfrey line are also very different from a function space perspective. The function space $C_p(\mathbb{R})$ has a whole host of nice properties: normal, Lindelof (hence paracompact and collectionwise normal), hereditarily Lindelof (hence hereditarily normal), hereditarily separable, and perfectly normal (discussed here).

Though separable, the function space $C_p(\mathbb{S})$ contains a closed and discrete subspace of cardinality continuum, making it not hereditarily separable and not normal.

For more information about $C_p(X)$ in general and $C_p(\mathbb{S})$ in particular, see [1] and [2]. A different proof that $C_p(\mathbb{S})$ contains a closed and discrete subspace of cardinality continuum can be found in Problem 165 in [2].

The next post is a continuation on the theme of drawing Sorgenfrey continuous functions.

Reference

Arkhangelskii, A. V., Topological Function Spaces, Mathematics and Its Applications Series, Kluwer Academic Publishers, Dordrecht, 1992.
Tkachuk V. V., A $C_p$ -Theory Problem Book, Topological and Function Spaces, Springer, New York, 2011.

$\text{ }$

$\copyright$ 2017 – Dan Ma

Normal dense subspaces of a product of “continuum” many separable metric factors

Posted on April 18, 2014 by Dan Ma

Is every normal dense subspace of a product of separable metric spaces collectionwise normal? This question was posed by Arkhangelskii in [1] (see Problem I.5.25). A partial positive answer is provided by a theorem that is usually attributed to Corson: If $Y$ is a normal dense subspace of a product of separable metric spaces and if $Y \times Y$ is also normal, then $Y$ is collectionwise normal. In this post, using a simple combinatorial argument, we show that any normal dense subspace of a product of continuum many separable metric space is collectionwise normal (see Corollary 4 below), which is a corollary of the following theorem.

Theorem 1
Let $X$ be a normal space with character $\le 2^\omega$ . If $2^\omega<2^{\omega_1}$ , then the following holds:

If $Y$ is a closed and discrete subspace of $X$ with $\lvert Y \lvert=\omega_1$ , then $Y$ contains a separated subset of cardinality $\omega_1$ .

Theorem 1 gives the corollary indicated at the beginning and several other interesting results. The statement $2^\omega<2^{\omega_1}$ means that the cardinality of the power set (the set of all subsets) of $\omega$ is strictly less than the cardinality of the power set of $\omega_1$ . Note that the statement $2^\omega<2^{\omega_1}$ follows from the continuum hypothesis (CH), the statement that $2^\omega=\omega_1$ . With the assumption $2^\omega<2^{\omega_1}$ , Theorem 1 is a theorem that goes beyond ZFC. We also present an alternative to Theorem 1 that removes the assumption $2^\omega<2^{\omega_1}$ (see Theorem 6 below).

A subset $T$ of a space $S$ is a separated set (in $S$ ) if for each $t \in T$ , there is an open subset $O_t$ of $S$ with $t \in O_t$ such that $\left\{O_t: t \in T \right\}$ is a pairwise disjoint collection. First we prove Theorem 1 and then discuss the corollaries.

____________________________________________________________________

Proof of Theorem 1

Suppose $Y$ is a closed and discrete subset of $X$ with $\lvert Y \lvert=\omega_1$ such that no subset of $Y$ of cardinality $\omega_1$ can be separated. We then show that $2^{\omega_1} \le 2^{\omega}$ .

For each $y \in Y$ , let $\mathcal{B}_y$ be a local base at the point $y$ such that $\lvert \mathcal{B}_y \lvert \le 2^\omega$ . Let $\mathcal{B}=\bigcup_{y \in Y} \mathcal{B}_y$ . Thus $\lvert \mathcal{B} \lvert \le 2^\omega$ . By normality, for each $W \subset Y$ , let $U_W$ be an open subset of $X$ such that $W \subset U_W$ and $\overline{U_W} \cap (Y-W)=\varnothing$ . For each $W \subset Y$ , consider the following collection of open sets:

$\mathcal{G}_W=\left\{V \in \mathcal{B}_y: y \in W \text{ and } V \subset U_W \right\}$

For each $W \subset Y$ , choose a maximal disjoint collection $\mathcal{M}_W$ of open sets in $\mathcal{G}_W$ . Because no subset of $Y$ of cardinality $\omega_1$ can be separated, each $\mathcal{M}_W$ is countable. If $W_1 \ne W_2$ , then $\mathcal{M}_{W_1} \ne \mathcal{M}_{W_2}$ .

Let $\mathcal{P}(Y)$ be the power set (i.e. the set of all subsets) of $Y$ . Let $\mathcal{P}_\omega(\mathcal{B})$ be the set of all countable subsets of $\mathcal{B}$ . Then the mapping $W \mapsto \mathcal{M}_W$ is a one-to-one map from $\mathcal{P}(Y)$ into $\mathcal{P}_\omega(\mathcal{B})$ . Note that $\lvert \mathcal{P}(Y) \lvert=2^{\omega_1}$ . Also note that since $\lvert \mathcal{B} \lvert \le 2^\omega$ , $\lvert \mathcal{P}_\omega(\mathcal{B}) \lvert \le 2^\omega$ . Thus $2^{\omega_1} \le 2^{\omega}$ . $\blacksquare$

____________________________________________________________________

Some Corollaries of Theorem 1

Here’s some corollaries that follow easily from Theorem 1. A space $X$ has the countable chain condition (CCC) if every pairwise disjoint collection of non-empty open subset of $X$ is countable. For convenience, if $X$ has the CCC, we say $X$ is CCC. The following corollaries make use of the fact that any normal space with countable extent is collectionwise normal (see Theorem 2 in this previous post).

Corollary 2
Let $X$ be a CCC space with character $\le 2^\omega$ . If $2^\omega<2^{\omega_1}$ , then the following conditions hold:

If $X$ is normal, then every closed and discrete subset of $X$ is countable, i.e., $X$ has countable extent.
If $X$ is normal, then $X$ is collectionwise normal.

Corollary 3
Let $X$ be a CCC space with character $\le 2^\omega$ . If CH holds, then the following conditions hold:

If $X$ is normal, then every closed and discrete subset of $X$ is countable, i.e., $X$ has countable extent.
If $X$ is normal, then $X$ is collectionwise normal.

Corollary 4
Let $X=\prod_{\alpha<2^\omega} X_\alpha$ be a product where each factor $X_\alpha$ is a separable metric space. If $2^\omega<2^{\omega_1}$ , then the following conditions hold:

If $Y$ is a normal dense subspace of $X$ , then $Y$ has countable extent.
If $Y$ is a normal dense subspace of $X$ , then $Y$ is collectionwise normal.

Corollary 4 is the result indicated in the title of the post. The product of separable spaces has the CCC. Thus the product space $X$ and any dense subspace of $X$ have the CCC. Because $X$ is a product of continuum many separable metric spaces, $X$ and any subspace of $X$ have characters $\le 2^\omega$ . Then Corollary 4 follows from Corollary 2.

When dealing with the topic of normal versus collectionwise normal, it is hard to avoid the connection with the normal Moore space conjecture. Theorem 1 gives the result of F. B. Jones from 1937 (see [3]). We have the following theorem.

Theorem 5
If $2^\omega<2^{\omega_1}$ , then every separable normal Moore space is metrizable.

Though this was not how Jones proved it in [3], Theorem 5 is a corollary of Corollary 2. By Corollary 2, any separable normal Moore space is collectionwise normal. It is well known that collectionwise normal Moore space is metrizable (Bing’s metrization theorem, see Theorem 5.4.1 in [2]).

____________________________________________________________________

A ZFC Theorem

We now prove a result that is similar to Corollary 2 but uses no set-theory beyond the Zermelo–Fraenkel set theory plus axiom of choice (abbreviated by ZFC). Of course the conclusion is not as strong. Even though the assumption $2^\omega<2^{\omega_1}$ is removed in Theorem 6, note the similarity between the proof of Theorem 1 and the proof of Theorem 6.

Theorem 6
Let $X$ be a CCC space with character $\le 2^\omega$ . Then the following conditions hold:

If $X$ is normal, then every closed and discrete subset of $X$ has cardinality less than continuum.

Proof of Theorem 6
Let $X$ be a normal CCC space with character $\le 2^\omega$ . Let $Y$ be a closed and discrete subset of $X$ . We show that $\lvert Y \lvert < 2^\omega$ . Suppose that $\lvert Y \lvert = 2^\omega$ .

For each $y \in Y$ , let $\mathcal{B}_y$ be a local base at the point $y$ such that $\lvert \mathcal{B}_y \lvert \le 2^\omega$ . Let $\mathcal{B}=\bigcup_{y \in Y} \mathcal{B}_y$ . Thus $\lvert \mathcal{B} \lvert = 2^\omega$ . By normality, for each $W \subset Y$ , let $U_W$ be an open subset of $X$ such that $W \subset U_W$ and $\overline{U_W} \cap (Y-W)=\varnothing$ . For each $W \subset Y$ , consider the following collection of open sets:

$\mathcal{G}_W=\left\{V \in \mathcal{B}_y: y \in W \text{ and } V \subset U_W \right\}$

For each $W \subset Y$ , choose $\mathcal{M}_W \subset \mathcal{G}_W$ such that $\mathcal{M}_W$ is a maximal disjoint collection. Since $X$ is CCC, $\mathcal{M}_W$ is countable. It is clear that if $W_1 \ne W_2$ , then $\mathcal{M}_{W_1} \ne \mathcal{M}_{W_2}$ .

Let $\mathcal{P}(Y)$ be the power set (i.e. the set of all subsets) of $Y$ . Let $\mathcal{P}_\omega(\mathcal{B})$ be the set of all countable subsets of $\mathcal{B}$ . Then the mapping $W \mapsto \mathcal{M}_W$ is a one-to-one map from $\mathcal{P}(Y)$ into $\mathcal{P}_\omega(\mathcal{B})$ . Note that since $\lvert \mathcal{B} \lvert = 2^\omega$ , $\lvert \mathcal{P}_\omega(\mathcal{B}) \lvert = 2^\omega$ . Thus $\lvert \mathcal{P}(Y) \lvert \le 2^{\omega}$ . However, $Y$ is assumed to be of cardinality continuum. Then $\lvert \mathcal{P}(Y) \lvert>2^{\omega_1}$ , leading to a contradiction. Thus it must be the case that $\lvert Y \lvert < 2^\omega$ . $\blacksquare$

With Theorem 6, Corollary 3 still holds. Theorem 6 removes the set-theoretic assumption of $2^\omega<2^{\omega_1}$ . As a result, the upper bound for cardinalities of closed and discrete sets is (at least potentially) higher.

____________________________________________________________________

Reference

Arkhangelskii, A. V., Topological Function Spaces, Mathematics and Its Applications Series, Kluwer Academic Publishers, Dordrecht, 1992.
Engelking, R., General Topology, Revised and Completed edition, Heldermann Verlag, Berlin, 1989.
Jones, F. B., Concerning normal and completely normal spaces, Bull. Amer. Math. Soc., 43, 671-677, 1937.

____________________________________________________________________

Looking for another closed and discrete subspace of a product space

Posted on April 16, 2014 by Dan Ma

Let $\omega_1$ be the first uncountable ordinal. In a previous post called Looking for a closed and discrete subspace of a product space, it was shown that the product space $\mathbb{R}^c$ , the product of continuum many copies of the real line $\mathbb{R}$ , contains a closed and discrete subset of cardinality continuum. This example shows that a product space of uncountably many copies of a “nice” space is “big and wide” enough to hide uncountable closed and discrete sets even when the product space is separable. This post reinforces this same fact by showing that $\mathbb{R}^{\omega_1}$ contains a closed and discrete subset of cardinality $\omega_1$ . It follows that for any uncountable cardinal $\tau$ , the product space $\mathbb{R}^\tau$ contains an uncountable closed and discrete subset, i.e., the product of uncountably many copies of the real line $\mathbb{R}$ has uncountable extent.

Let $\omega$ be the first infinite ordinal, i.e., the set of all nonnegative integers. Consider $\omega^{\omega_1}$ , the product of $\omega_1$ many copies of $\omega$ with the discrete topology. Since $\omega^{\omega_1}$ is a closed subspace of $\mathbb{R}^{\omega_1}$ , it suffices to show that $\omega^{\omega_1}$ has an uncountable closed and discrete subset.

____________________________________________________________________

The Construction

We now construct an uncountable closed and discrete subset of $\omega^{\omega_1}$ . Let $\delta$ be an infinite ordinal such that $\omega<\delta<\omega_1$ . Let $W=\left\{\alpha: \delta \le \alpha<\omega_1 \right\}$ . For each $\alpha \in W$ , let $Y_\alpha=\left\{\beta<\omega_1: \beta<\alpha \right\}$ . We can also use interval notations: $W=[\delta,\omega_1)$ and $Y_\alpha=[0,\alpha)$ . Consider $Y_\alpha$ as a space with the discrete topology. Then it is clear that $\omega^{\omega_1}$ is homeomorphic to the product space $\prod_{\alpha \in W} Y_\alpha$ . Thus the focus is now on finding an uncountable closed and discrete subset of $\prod_{\alpha \in W} Y_\alpha$ .

One interesting fact about the space $\prod_{\alpha \in W} Y_\alpha$ is that every function $f \in \prod_{\alpha \in W} Y_\alpha$ is a pressing down function. That is, for every $f \in \prod_{\alpha \in W} Y_\alpha$ , $f(\alpha)<\alpha$ for all $\alpha \in W$ . Note that $f$ is defined on $W$ , a closed and unbounded subset of $\omega_1$ (hence a stationary set). It follows that for each $f \in \prod_{\alpha \in W} Y_\alpha$ , there is a stationary set $S \subset W$ and there exists $\rho<\omega_1$ such that $f(\alpha)=\rho$ for all $\alpha \in S$ . This fact is called the pressing down lemma and will be used below. See this post for more information about the pressing down lemma.

For each $\gamma \in W$ , let $h_\gamma: Y_{\gamma+1} \rightarrow \delta$ be a one-to-one function. For each $\gamma \in W$ , define $t_\gamma \in \prod_{\alpha \in W} Y_\alpha$ as follows:

$t_\gamma(\alpha) = \begin{cases} h_\gamma(\alpha) & \mbox{if } \delta \le \alpha \le \gamma \\ \gamma & \mbox{if } \gamma < \alpha <\omega_1 \end{cases}$

Note that each $t_\gamma$ is a pressing down function. Thus each $t_\gamma \in \prod_{\alpha \in W} Y_\alpha$ . Let $T=\left\{t_\gamma: \gamma \in W \right\}$ . Clearly $t_\gamma \ne t_\mu$ if $\gamma \ne \mu$ . Thus $T$ has cardinality $\omega_1$ . We claim that $T$ is a closed and discrete subset of $\prod_{\alpha \in W} Y_\alpha$ . It suffices to show that for each $f \in \prod_{\alpha \in W} Y_\alpha$ , there exists an open set $V$ with $f \in V$ such that $V$ contains at most one $t_\gamma$ .

Let $f \in \prod_{\alpha \in W} Y_\alpha$ . As discussed above, there is a stationary set $S \subset W$ and there exists $\rho<\omega_1$ such that $f(\alpha)=\rho$ for all $\alpha \in S$ . In particular, choose $\mu, \lambda \in S$ such that $\mu \ne \lambda$ . Thus $f(\mu)=f(\lambda)=\rho$ . Let $V$ be the open set defined by:

$V=\left\{g \in \prod_{\alpha \in W} Y_\alpha: g(\mu)=g(\lambda)=\rho \right\}$

Clearly, $f \in V$ . We show that if $t_\gamma \in V$ , then $\gamma=\rho$ . Suppose $t_\gamma \in V$ . Then $t_\gamma(\mu)=t_\gamma(\lambda)=\rho$ . Consider two cases: Case 1: $\delta \le \mu, \lambda \le \gamma$ ; Case 2: one of $\mu$ and $\lambda>\gamma$ . The definition of $t_\gamma$ indicates that $t_\gamma=h_\gamma$ on the interval $[\delta, \gamma]$ . Note that $h_\gamma$ is a one-to-one function. Since $t_\gamma(\mu)=t_\gamma(\lambda)$ , it cannot be that $\mu, \lambda \in [\delta, \gamma]$ , i.e., Case 1 is not possible. Thus Case 2 holds, say $\mu>\gamma$ . Then by definition, $t_\gamma(\mu)=\gamma$ . Putting everything together, $\gamma=t_\gamma(\mu)=t_\gamma(\lambda)=\rho$ . Thus $V \cap T \subset \left\{t_\rho \right\}$ . This concludes the proof that the set $T$ is a closed and discrete subset of $\prod_{\alpha \in W} Y_\alpha$ . $\blacksquare$