Recall the product space of the Michael line and the space of the irrational numbers. Even though the first factor is a normal space (in fact a paracompact space) and the second factor is a metric space, their product space is not normal. This is one of the classic examples demonstrating that normality is not well behaved with respect to product space. This post presents an even more striking result, i.e., for any non-discrete normal space  , there exists another normal space
, there exists another normal space  such that
such that  is not normal. The example of the non-normal product of the Michael line and the irrationals is not some isolated example. Rather it is part of a wide spread phenomenon. This result guarantees that no matter how nice a space
is not normal. The example of the non-normal product of the Michael line and the irrationals is not some isolated example. Rather it is part of a wide spread phenomenon. This result guarantees that no matter how nice a space  is, a counter part
is, a counter part  can always be found that the product of the two spaces is not normal. This result is known as Morita’s first conjecture and was proved by Atsuji and Rudin. The solution is based on a generalization of Dowker’s theorem and a construction done by Rudin. This post demonstrates how the solution is put together.
can always be found that the product of the two spaces is not normal. This result is known as Morita’s first conjecture and was proved by Atsuji and Rudin. The solution is based on a generalization of Dowker’s theorem and a construction done by Rudin. This post demonstrates how the solution is put together.
All spaces under consideration are Hausdorff.
____________________________________________________________________
Morita’s First Conjecture
In 1976, K. Morita posed the following conjecture.
Morita’s First Conjecture
If  is a normal space such that
is a normal space such that  is a normal space for every normal space
is a normal space for every normal space  , then
, then  is a discrete space.
is a discrete space.
The proof given in this post is for proving the contrapositive of the above statement.
Morita’s First Conjecture
If  is a non-discrete normal space, then there exists some normal space
is a non-discrete normal space, then there exists some normal space  such that
such that  is not a normal space.
is not a normal space.
Though the two forms are logically equivalent, the contrapositive form seems to have a bigger punch. The contrapositive form gives an association. Each non-discrete normal space is paired with a normal space to form a non-normal product. Examples of such pairings are readily available. Michael line is paired with the space of the irrational numbers (as discussed above). The Sogenfrey line is paired with itself. The first uncountable ordinal  is paired with
is paired with 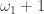 (see here) or paired with the cube
(see here) or paired with the cube  where
where ![I=[0,1]](https://s0.wp.com/latex.php?latex=I%3D%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) with the usual topology (see here). There are plenty of other individual examples that can be cited. In this post, we focus on a constructive proof of finding such a pairing.
with the usual topology (see here). There are plenty of other individual examples that can be cited. In this post, we focus on a constructive proof of finding such a pairing.
Since the conjecture had been affirmed positively, it should no longer be called a conjecture. Calling it Morita’s first theorem is not appropriate since there are other results that are identified with Morita. In this discussion, we continue to call it a conjecture. Just know that it had been proven.
____________________________________________________________________
Dowker’s Theorem
Next, we examine Dowker’s theorem, which characterizes normal countably paracompact spaces. The following is the statement.
Theorem 1 (Dowker’s Theorem)
Let  be a normal space. The following conditions are equivalent.
be a normal space. The following conditions are equivalent.
- The space
 is countably paracompact.
is countably paracompact.
- Every countable open cover of
 has a point-finite open refinement.
has a point-finite open refinement.
- If
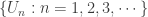 is an open cover of
is an open cover of  , there exists an open refinement
, there exists an open refinement 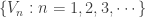 such that
such that 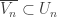 for each
for each  .
.
- The product space
 is normal for any compact metric space
is normal for any compact metric space  .
.
- The product space
![X \times [0,1]](https://s0.wp.com/latex.php?latex=X+%5Ctimes+%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) is normal where
is normal where ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) is the closed unit interval with the usual Euclidean topology.
is the closed unit interval with the usual Euclidean topology.
- For each sequence
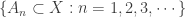 of closed subsets of
of closed subsets of  such that
such that  and
and  , there exist open sets
, there exist open sets  such that
such that  for each
for each  such that
such that  .
.
The theorem is discussed here and proved here. Any normal space that violates any one of the conditions in the theorem is said to be a Dowker space. One such space was constructed by Rudin in 1971 [2]. Any Dowker space would be one factor in a non-normal product space with the other factor being a compact metric space. Actually much more can be said.
The Dowker space constructed by Rudin is the solution of Morita’s conjecture for a large number of spaces. At minimum, the product of any infinite compact metric space and the Dowker space is not normal as indicated by Dowker’s theorem. Any nontrivial convergent sequence plus the limit point is a compact metric space since it is homeomorphic to 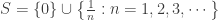 (as a subspace of the real line). Thus Rudin’s Dowker space has non-normal product with
(as a subspace of the real line). Thus Rudin’s Dowker space has non-normal product with  . Furthermore, the product of Rudin’s Dowker space and any space containing a copy of
. Furthermore, the product of Rudin’s Dowker space and any space containing a copy of  is not normal.
is not normal.
Spaces that contain a copy of  extend far beyond the compact metric spaces. Spaces that have lots of convergent sequences include first countable spaces, Frechet spaces and many sequential spaces (see here for an introduction for these spaces). Thus any Dowker space is an answer to Morita’s first conjecture for the non-discrete members of these classes of spaces. Actually, the range for the solution is wider than these spaces. It turns out that any space that has a countable non-discrete subspace would have a non-normal product with a Dowker space. These would include all the classes mentioned above (first countable, Frechet, sequential) as well as countably tight spaces and more.
extend far beyond the compact metric spaces. Spaces that have lots of convergent sequences include first countable spaces, Frechet spaces and many sequential spaces (see here for an introduction for these spaces). Thus any Dowker space is an answer to Morita’s first conjecture for the non-discrete members of these classes of spaces. Actually, the range for the solution is wider than these spaces. It turns out that any space that has a countable non-discrete subspace would have a non-normal product with a Dowker space. These would include all the classes mentioned above (first countable, Frechet, sequential) as well as countably tight spaces and more.
Therefore, any Dowker space, a normal space that is not countably paracompact, is severely lacking in ability in forming normal product with another space. In order to obtain a complete solution to Morita’s first conjecture, we would need a generalized Dowker’s theorem.
____________________________________________________________________
Shrinking Properties
The key is to come up with a generalized Dowker’s theorem, a theorem like Theorem 1 above, except that it is for arbitrary infinite cardinality. Then a  -Dowker space is a space that violates one condition in the theorem. That space would be a candidate for the solution of Morita’s first conjecture. Note that Theorem 1 is for the infinite countable cardinal
-Dowker space is a space that violates one condition in the theorem. That space would be a candidate for the solution of Morita’s first conjecture. Note that Theorem 1 is for the infinite countable cardinal  only. Before stating the theorem, let’s gather all the notions that will go into the theorem.
only. Before stating the theorem, let’s gather all the notions that will go into the theorem.
Let  be a space. Let
be a space. Let  be an open cover of the space
be an open cover of the space  . The open cover
. The open cover  is said to be shrinkable if there is an open cover
is said to be shrinkable if there is an open cover  such that
such that 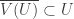 for each
for each 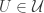 . When this is the case, the open cover
. When this is the case, the open cover  is said to be a shrinking of
is said to be a shrinking of  . If an open cover is shrinkable, we also say that the open cover can be shrunk (or has a shrinking).
. If an open cover is shrinkable, we also say that the open cover can be shrunk (or has a shrinking).
Let  be a cardinal. The space
be a cardinal. The space  is said to be a
is said to be a  -shrinking space if every open cover of cardinality
-shrinking space if every open cover of cardinality 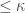 of the space
of the space  is shinkable. The space
is shinkable. The space  is a shrinking space if it is a
is a shrinking space if it is a  -shrinking space for every cardinal
-shrinking space for every cardinal  .
.
When a family of sets are indexed by ordinals, the notion of an increasing or decreasing family of sets is possible. For example, the family 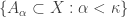 of subsets of the space
of subsets of the space  is said to be increasing if
is said to be increasing if 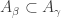 whenever
whenever 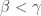 . In other words, for an increasing family, the sets are getting larger whenever the index becomes larger. A decreasing family of sets is defined in the reverse way. These two notions are important for some shrinking properties discussed here – e.g. using an open cover that is increasing or using a family of closed sets that is decreasing.
. In other words, for an increasing family, the sets are getting larger whenever the index becomes larger. A decreasing family of sets is defined in the reverse way. These two notions are important for some shrinking properties discussed here – e.g. using an open cover that is increasing or using a family of closed sets that is decreasing.
In the previous discussion on shrinking spaces, two other shrinking properties are discussed – property  and property
and property  . A space
. A space  is said to have property
is said to have property  if every increasing open cover of cardinality
if every increasing open cover of cardinality 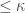 for the space
for the space  is shrinkable. A space
is shrinkable. A space  is said to have property
is said to have property  if every increasing open cover of cardinality
if every increasing open cover of cardinality 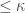 for the space
for the space  has a shrinking that is increasing. See this previous post for a discussion on property
has a shrinking that is increasing. See this previous post for a discussion on property 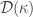 and property
and property  .
.
____________________________________________________________________
An Attempt for a Generalized Dowker’s Theorem
Let  be an infinite cardinal. The space
be an infinite cardinal. The space  is said to be a
is said to be a  -paracompact space if every open cover
-paracompact space if every open cover  of
of  with
with 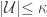 has a locally finite open refinement. Thus a space is paracompact if it is
has a locally finite open refinement. Thus a space is paracompact if it is  -paracompact for every infinite cardinal
-paracompact for every infinite cardinal  . Of course, an
. Of course, an  -paracompact space is a countably paracompact space.
-paracompact space is a countably paracompact space.
For any infinite  , let
, let  be a discrete space of size
be a discrete space of size  . Let
. Let  be a point not in
be a point not in  . Define the space
. Define the space 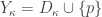 as follows. The subspace
as follows. The subspace  is discrete as before. The open neighborhoods at
is discrete as before. The open neighborhoods at  are of the form
are of the form 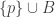 where
where  and
and 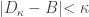 . In other words, any open set containing
. In other words, any open set containing  contains all but less than
contains all but less than  many discrete points.
many discrete points.
Another concept that is needed is the cardinal function called minimal tightness. Let  be any space. Define the minimal tightness
be any space. Define the minimal tightness  as the least infinite cardinal
as the least infinite cardinal  such that there is a non-discrete subspace of
such that there is a non-discrete subspace of  of cardinality
of cardinality  . If
. If  is a discrete space, then let
is a discrete space, then let 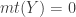 . For any non-discrete space
. For any non-discrete space  ,
, 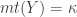 for some infinite
for some infinite  . Note that for the space
. Note that for the space 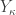 defined above would have
defined above would have 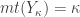 . For any space
. For any space  ,
,  if and only if
if and only if  has a countable non-discrete subspace.
has a countable non-discrete subspace.
The following theorem can be called a  -Dowker’s Theorem.
-Dowker’s Theorem.
Theorem 2
Let  be a normal space. Let
be a normal space. Let  be an infinite cardinal. Consider the following conditions.
be an infinite cardinal. Consider the following conditions.
- The space
 is a
is a  -paracompact space.
-paracompact space.
- The space
 is a
is a  -shrinking space.
-shrinking space.
- For each open cover
 of
of  , there exists an open cover
, there exists an open cover 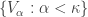 such that
such that 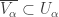 for each
for each 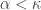 .
.
- The space
 has property
has property 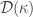 .
.
- For each increasing open cover
 of
of  , there exists an open cover
, there exists an open cover 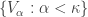 such that
such that 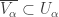 for each
for each 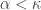 .
.
- For each decreasing family
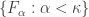 of closed subsets of
of closed subsets of  such that
such that 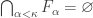 , there exists a family
, there exists a family 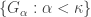 of open subsets of
of open subsets of  such that
such that  and
and 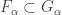 for each
for each 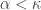 .
.
- The space
 has property
has property  .
.
- For each increasing open cover
 of
of  , there exists an increasing open cover
, there exists an increasing open cover 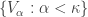 such that
such that 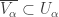 for each
for each 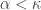 .
.
- The product space
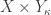 is a normal space.
is a normal space.
- The product space
 is a normal space for some space
is a normal space for some space  with
with 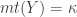 .
.
The following diagram shows how these conditions are related.
Diagram 1

In addition to Diagram 1, we have the relations  and
and  .
.
Remarks
At first glance, Diagram 1 might give the impression that the conditions in the theorem form a loop. It turns out the strongest property is  -paracompactness (condition 1). Since condition 2 does not imply condition 5, condition 2 does not imply condition 1. Thus the conditions do not form a loop.
-paracompactness (condition 1). Since condition 2 does not imply condition 5, condition 2 does not imply condition 1. Thus the conditions do not form a loop.
The implications 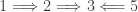 and
and 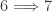 are immediate. The following implications are established in this previous post.
are immediate. The following implications are established in this previous post.
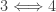 (Theorem 4)
(Theorem 4)
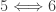 (Theorem 7)
(Theorem 7)
 (Example 1)
(Example 1)
The remaining implications to be shown are 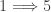 and
and 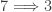 .
.
____________________________________________________________________
Proof of Theorem 2
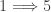
Let 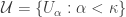 be an increasing open cover of
be an increasing open cover of  . By
. By  -paracompactness, let
-paracompactness, let  be a locally finite open refinement of
be a locally finite open refinement of  . For each
. For each 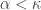 , define
, define 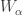 as follows:
as follows:
Then  is still a locally finite refinement of
is still a locally finite refinement of  . Since the space
. Since the space  is normal, any locally finite open cover is shrinkable. Let
is normal, any locally finite open cover is shrinkable. Let 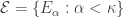 be a shrinking of
be a shrinking of  . The open cover
. The open cover 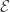 is also locally finite. For each
is also locally finite. For each  , let
, let  . Then
. Then 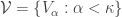 is an increasing open cover of
is an increasing open cover of  . Note that
. Note that
since 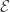 is locally finite and thus closure preserving. Since
is locally finite and thus closure preserving. Since  is increasing,
is increasing,  for all
for all 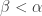 . This means that
. This means that 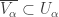 for all
for all  .
.
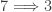
Since condition 3 is equivalent to condition 4, we show  . Suppose that
. Suppose that  is normal where
is normal where  is a space such that
is a space such that 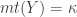 . Let
. Let 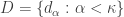 be a non-discrete subset of
be a non-discrete subset of  . Let
. Let  be a point such that
be a point such that 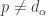 for all
for all  and such that
and such that  is a limit point of
is a limit point of  (this means that every open set containing
(this means that every open set containing  contains some
contains some  ). Let
). Let 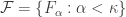 be a decreasing family of closed subsets of
be a decreasing family of closed subsets of  such that
such that 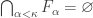 . Define
. Define  and
and  as follows:
as follows:
The sets  and
and  are clearly disjoint. The set
are clearly disjoint. The set  is clearly a closed subset of
is clearly a closed subset of  . To show that
. To show that  is closed, let
is closed, let 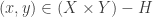 . Two cases to consider:
. Two cases to consider: 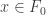 or
or 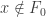 where
where  is the first closed set in the family
is the first closed set in the family  .
.
The first case 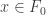 . Let
. Let 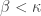 be least such that
be least such that 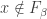 . Then
. Then 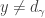 for all
for all  since
since 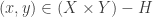 . In the space
. In the space  , any subset of cardinality
, any subset of cardinality  is a closed set. Let
is a closed set. Let 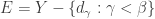 , which is open containing
, which is open containing  . Let
. Let  be open such that
be open such that  and
and  . Then
. Then  and
and  misses points of
misses points of  .
.
Now consider the second case 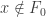 . Let
. Let 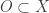 be open such that
be open such that  and
and 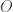 misses
misses  . Then
. Then 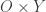 is an open set containing
is an open set containing 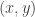 such that
such that 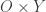 misses
misses  . Thus
. Thus  is a closed subset of
is a closed subset of  .
.
Since  is normal, choose open
is normal, choose open 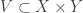 such that
such that 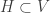 and
and 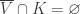 . For each
. For each 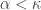 , define
, define 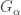 as follows:
as follows:
Note that each 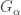 is open in
is open in  and that
and that 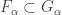 for each
for each 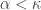 . We claim that
. We claim that  . Let
. Let 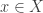 . The point
. The point 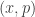 is in
is in  . Thus
. Thus 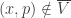 . Choose an open set
. Choose an open set  such that
such that 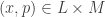 and
and  . Since
. Since 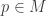 , there is some
, there is some 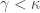 such that
such that 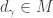 . Since
. Since 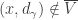 ,
,  . Thus
. Thus 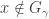 . This establishes the claim that
. This establishes the claim that  .
.
____________________________________________________________________
 -Dowker Space
-Dowker Space
Analogous to the Dowker space, a  -Dowker space is a normal space that violates one condition in Theorem 2. Since the seven conditions listed in Theorem 7 are not all equivalent, which condition to use? Condition 1 is the strongest condition since it implies all the other condition. At the lower left corner of Diagram 1 is condition 3, which follows from every other condition. Thus condition 3 (or 4) is the weakest property. An appropriate definition of a
-Dowker space is a normal space that violates one condition in Theorem 2. Since the seven conditions listed in Theorem 7 are not all equivalent, which condition to use? Condition 1 is the strongest condition since it implies all the other condition. At the lower left corner of Diagram 1 is condition 3, which follows from every other condition. Thus condition 3 (or 4) is the weakest property. An appropriate definition of a  -Dowker space is through negating condition 3 or condition 4. Thus, given an infinite cardinal
-Dowker space is through negating condition 3 or condition 4. Thus, given an infinite cardinal  , a
, a  -Dowker space is a normal space
-Dowker space is a normal space  that satisfies the following condition:
that satisfies the following condition:
There exists a decreasing family 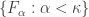 of closed subsets of
of closed subsets of  with
with 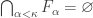 such that for every family
such that for every family 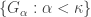 of open subsets of
of open subsets of  with
with 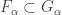 for each
for each  ,
, 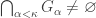 .
.
The definition of  -Dowker space is through negating condition 4. Of course, negating condition 3 would give an equivalent definition.
-Dowker space is through negating condition 4. Of course, negating condition 3 would give an equivalent definition.
When  is the countably infinite cardinal
is the countably infinite cardinal  , a
, a  -Dowker space is simply the ordinary Dowker space constructed by M. E. Rudin [2]. Rudin generalized the construction of the ordinary Dowker space to obtain a
-Dowker space is simply the ordinary Dowker space constructed by M. E. Rudin [2]. Rudin generalized the construction of the ordinary Dowker space to obtain a  -Dowker space for every infinite cardinal
-Dowker space for every infinite cardinal  [4]. The space that Rudin constructed in [4] would be a normal space
[4]. The space that Rudin constructed in [4] would be a normal space  such that condition 4 of Theorem 2 is violated. This means that the space
such that condition 4 of Theorem 2 is violated. This means that the space  would violate condition 7 in Theorem 2. Thus
would violate condition 7 in Theorem 2. Thus  is not normal for every space
is not normal for every space  with
with 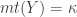 .
.
Here’s the solution of Morita’s first conjecture. Let  be a normal and non-discrete space. Determine the least cardinality
be a normal and non-discrete space. Determine the least cardinality  of a non-discrete subspace of
of a non-discrete subspace of  . Obtain the
. Obtain the  -Dowker space
-Dowker space  as in [4]. Then
as in [4]. Then  is not normal according to the preceding paragraph.
is not normal according to the preceding paragraph.
____________________________________________________________________
Remarks
Answering Morita’s first conjecture is a two-step approach. First, figure out what a generalized Dowker’s theorem should be. Then a  -Dowker space is one that violates an appropriate condition in the generalized Dowker’s theorem. By violating the right condition in the theorem, we have a way to obtain non-normal product space needed in the answer. The second step is of course the proof of the existence of a space that violates the condition in the generalized Dowker’s theorem.
-Dowker space is one that violates an appropriate condition in the generalized Dowker’s theorem. By violating the right condition in the theorem, we have a way to obtain non-normal product space needed in the answer. The second step is of course the proof of the existence of a space that violates the condition in the generalized Dowker’s theorem.
Figuring out the form of the generalized Dowker’s theorem took some work. It is more than just changing the countable infinite cardinal in Dowker’s theorem (Theorem 1 above) to an arbitrary infinite cardinal. This is because the conditions in Theorem 1 are unequal when the cardinality is changed to an uncountable one.
We take the cue from Rudin’s chapter on Dowker spaces [3]. In the last page of that chapter, Rudin pointed out the conditions that should go into a generalized Dowker’s theorem. However, the explanation of the relationship among the conditions is not clear. The previous post and this post are an attempt to sort out the conditions and fill in as much details as possible.
Rudin’s chapter did have the right condition for defining  -Dowker space. It seems that prior to the writing of that chapter, there was some confusion on how to define a
-Dowker space. It seems that prior to the writing of that chapter, there was some confusion on how to define a  -Dowker space, i.e. a condition in the theorem the violation of which would give a
-Dowker space, i.e. a condition in the theorem the violation of which would give a  -Dowker space. If the condition used is a stronger property, the violation may not yield enough information to get non-normal products. According to Diagram 1, condition 3 in Theorem 2 is the right one to use since it is the weakest condition and is down streamed from the conditions about normal product space. So the violation of condition 3 would answer Morita’s first conjecture.
-Dowker space. If the condition used is a stronger property, the violation may not yield enough information to get non-normal products. According to Diagram 1, condition 3 in Theorem 2 is the right one to use since it is the weakest condition and is down streamed from the conditions about normal product space. So the violation of condition 3 would answer Morita’s first conjecture.
We do not discuss the other step in the solution in any details. Any interested reader can review Rudin’s construction in [2] and [4]. The  -Dowker space is an appropriate subspace of a product space with the box topology.
-Dowker space is an appropriate subspace of a product space with the box topology.
One interesting observation about the ordinary Dowker space (the one that violates a condition in Theorem 1) is that the product of any Dowker space and any space with a countable non-discrete subspace is not normal. This shows that Dowker space is badly non-productive with respect to normality. This fact is actually not obvious in the usual formulation of Dowker’s theorem (Theorem 1 above). What makes this more obvious in the direction 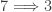 in Theorem 2. For the countably infinite case,
in Theorem 2. For the countably infinite case, 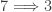 is essentially this: If
is essentially this: If  is normal where
is normal where  has a countable non-discrete subspace, then
has a countable non-discrete subspace, then  is not a Dowker space. Thus if the goal is to find a non-normal product space, a Dowker space should be one space to check.
is not a Dowker space. Thus if the goal is to find a non-normal product space, a Dowker space should be one space to check.
____________________________________________________________________
Loose Ends
In the course of working on the contents in this post and the previous post, there are some questions that we do not know how to answer and have not spent time to verify one way or the other. Possibly there are some loose ends to tie. They for the most parts are not open questions, but they should be interesting questions to consider.
For the  -Dowker’s theorem (Theorem 2), one natural question is on the relative strengths of the conditions. It will be interesting to find out the implications not shown in Diagram 1. For example, for the three shrinking properties (conditions 2, 3 and 5), it is straightforward from definition that
-Dowker’s theorem (Theorem 2), one natural question is on the relative strengths of the conditions. It will be interesting to find out the implications not shown in Diagram 1. For example, for the three shrinking properties (conditions 2, 3 and 5), it is straightforward from definition that 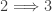 and
and  . The example of
. The example of  (the first uncountable ordinal) shows that
(the first uncountable ordinal) shows that  and hence
and hence 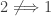 . What about
. What about 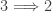 ? In [5], Beslagic and Rudin showed that
? In [5], Beslagic and Rudin showed that 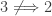 using
using  . A natural question would be: can there be ZFC example? Perhaps searching on more recent papers can yield some answers.
. A natural question would be: can there be ZFC example? Perhaps searching on more recent papers can yield some answers.
Another question is 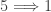 ? The answer is no with the example being a Navy space – Example 7.6 in p. 194 [1]. The other two directions that have not been accounted for are:
? The answer is no with the example being a Navy space – Example 7.6 in p. 194 [1]. The other two directions that have not been accounted for are:  and
and 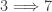 ? We do not know the answer.
? We do not know the answer.
Another small question that we come across is about  (the first uncountable ordinal). This is an example for showing
(the first uncountable ordinal). This is an example for showing  . Thus condition 6 is false. Thus
. Thus condition 6 is false. Thus  is not normal. Here
is not normal. Here  is simply the one-point Lindelofication of a discrete space of cardinality
is simply the one-point Lindelofication of a discrete space of cardinality  . The question is: is condition 7 true for
. The question is: is condition 7 true for  ? The product of
? The product of  and
and  (a space with minimal tightness
(a space with minimal tightness  ) is not normal. Is there a normal
) is not normal. Is there a normal  where
where  is another space with minimal tightness
is another space with minimal tightness  ?
?
Dowker’s theorem and  -Dowker’s theorem show that finding a normal space that is not shrinking is not a simple matter. To find a normal space that is not countably shrinking took 20 years (1951 to 1971). For any uncountable
-Dowker’s theorem show that finding a normal space that is not shrinking is not a simple matter. To find a normal space that is not countably shrinking took 20 years (1951 to 1971). For any uncountable  , the
, the  -Dowker space that is based on the same construction of an ordinary Dowker space is also a space that is not
-Dowker space that is based on the same construction of an ordinary Dowker space is also a space that is not  -shrinking. With an uncountable
-shrinking. With an uncountable  , is the
, is the  -Dowker space countably shrinking? This is not obvious one way or the other just from the definition of
-Dowker space countably shrinking? This is not obvious one way or the other just from the definition of  -Dowker space. Perhaps there is something obvious and we have not connected the dots. Perhaps we need to go into the definition of the
-Dowker space. Perhaps there is something obvious and we have not connected the dots. Perhaps we need to go into the definition of the  -Dowker space in [4] to show that it is countably shrinking. The motivation is that we tried to find a normal space that is countably shrinking but not
-Dowker space in [4] to show that it is countably shrinking. The motivation is that we tried to find a normal space that is countably shrinking but not  -shrinking for some uncountable
-shrinking for some uncountable  . It seems that the
. It seems that the  -Dowker space in [4] is the natural candidate.
-Dowker space in [4] is the natural candidate.
____________________________________________________________________
Reference
- Morita K., Nagata J.,Topics in General Topology, Elsevier Science Publishers, B. V., The Netherlands, 1989.
- Rudin M. E., A Normal Space
 for which
for which 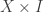 is not Normal, Fund. Math., 73, 179-486, 1971. (link)
is not Normal, Fund. Math., 73, 179-486, 1971. (link)
- Rudin M. E., Dowker Spaces, Handbook of Set-Theoretic Topology (K. Kunen and J. E. Vaughan, eds), Elsevier Science Publishers B. V., Amsterdam, (1984) 761-780.
- Rudin M. E.,
 -Dowker Spaces, Czechoslovak Mathematical Journal, 28, No.2, 324-326, 1978. (link)
-Dowker Spaces, Czechoslovak Mathematical Journal, 28, No.2, 324-326, 1978. (link)
- Rudin M. E., Beslagic A.,Set-Theoretic Constructions of Non-Shrinking Open Covers, Topology Appl., 20, 167-177, 1985. (link)
- Yasui Y., On the Characterization of the
 -Property by the Normality of Product Spaces, Topology and its Applications, 15, 323-326, 1983. (abstract and paper)
-Property by the Normality of Product Spaces, Topology and its Applications, 15, 323-326, 1983. (abstract and paper)
- Yasui Y., Some Characterization of a
 -Property, TSUKUBA J. MATH., 10, No. 2, 243-247, 1986.
-Property, TSUKUBA J. MATH., 10, No. 2, 243-247, 1986.
____________________________________________________________________
where the first factor
is the space of countable ordinals with the usual order topology and the second factor
is the product of continuum many copies of the unit interval
.
is not normal, a result not shown in Steen and Seebach. The proof that was given in this site (see here) is based on an article published in 1976 [1], long before the publication date of the first edition of Steen and Seebach in 1970. It turns out that the non-normality of
was given as an exercise in Steen and Seebach in the problem section at the end of the book (problem 127 in page 211, Dover edition). Problem 127: Show that
is not normal. This indicates that the result not shown in Steen and Seebach was because it was given as a problem and not because the tool for solving it was not yet available. The fact that it is given as an exercise also means that there is a more basic proof of the non-normality of
. So, once this is realized, I set out to find a simpler proof or at least one that does not rely on the result from [1]. Interestingly, this proof brings out a broader discussion that is worthwhile and goes beyond the example at hand. The goal here is to examine the more basic proof and the broader discussion.
and its immediate successor.
is the set of all countable ordinals with the order topology. The ordinal
is the immediate successor of
. It can be regarded as the result of adding one more point to
. The extra point is
, i.e.,
with
greater than all points
. The ordinal
with the order topology is a compact space. Using interval notation,
and
. As ordinals,
is the first uncountable ordinal and
is the first uncountable successor ordinal. For more information, see here.
is a classic example of a product of a normal space (the first factor) and a compact space (the second factor) that is not normal. This example and others like it show that normality is easily broken upon taking product even if one of the factors is as nice as a compact space. The non-normality of
is discussed here. In that proof, two disjoint closed sets
and
are given such that they cannot be separated by disjoint open sets. The
and
are:
is not normal, we show that one of its closed subspaces is not normal. That closed subspace is
. To this end, we show that
can be embedded in the product space
. With a non-normal closed subspace, it follows that
is not normal. The remainder of the proof is to give the embedding.
can be embedded as a closed subspace of
, the product of
many copies of
. This means that
is also a closed subspace of
.
, define
as follows:
by letting
for all
. Consider the correspondence
with
and
. The mapping is clearly one-to-one from
onto
. Upon closer inspection, the mapping in each direction is continuous (this is a good exercise to walk through). Thus, the mapping is a homeomorphism. It follows that
can be considered a subspace of
. Since
is compact, it must be a closed subspace. With the cardinality of
being less than or equal to continuum, it follows that
can be embedded as a closed subspace of
.
, i.e., the Stone-Cech compactification of the first uncountable ordinal is its immediate successor.
, note that every continuous function defined on
is bounded and is eventually constant (see result B here). As a result, every continuous function defined on
can be extended to a continuous function defined on
. For any continuous function
, we can simply define
to be the eventual constant value. A subspace
of a space
is
-embedded in
if every bounded continuous real-valued function on
can be extended to
. According to theorem 19.12 in [4], if
is a compactification of
and if
is
-embedded in
, then
is the Stone-Cech compactification of
. Thus
is
-embedded in
and
is the Stone-Cech compactification of
. In this instance, the Stone-Cech compactification agrees with the one-point compactification. Consider the following class theorem about normality in product space. The theorem is Corollary 3.4 in the chapter on products of normal spaces in the handbook of set-theoretic topology [2].
be a space. The following conditions are equivalent.
is paracompact.
is normal.
is due to the non-normality of
. Based on this theorem, the non-normality of
is due to the non-paracompactness of
. See result G here for a proof that
is not paracompact.
is not normal. One way is the basic proof indicated above. The other way is to use Theorem 1, along with the homeomorphic embedding from
into
, the fact that
and the fact that
is not paracompact. Both are valuable. The first way is basic and is a constructive proof. Because it is more hands-on, it is a better proof to learn from. The second way provides a broader perspective that is informative but requires quoting a couple of fairly deep results. Perhaps it is best used as a second proof for perspective.
contains a copy of
, then the product space
is not normal. The contrapositive statement would be the following:
be a space. If the product space
is normal, then
cannot contain a copy of
.
, note the following about the last point:
but
for any countable
, i.e., the last point is the limit point of the set of all the points preceding it but is not in the closure of any countable set. This means that the space
does not have countable tightness (or is not countably tight). See here for definition. The property of countable tightness is hereditary. If
contains a copy of
, then
is not countably tight (or is uncountably tight). This brings us to the following theorem.
be an infinite compact space. Then
is normal if and only if
has countable tightness.
and the second factor being a compact space, the real story is the tightness of that compact space. If the tightness is countable, the product is normal. Otherwise, the product is not normal. The theorem is another reason that
is not normal. Instead of embedding
into
, we can actually show that
does not have countable tightness. This is the approach that was taken in this previous post.
), see the chapter on products of normal spaces in the handbook of set-theoretic topology [2].
2021 – Dan Ma
