It is a well known result in general topology that in any regular space with the countable chain condition, paracompactness and the Lindelof property are equivalent. The proof of this result hinges on one theorem about the spaces with the countable chain condition. In this post we are to put the spotlight on this theorem (Theorem 1 below) and then use it to prove a few results. These results indicate that in a space with the countable chain condition with some weaker covering property is either Lindelof or paracompact.
This post is centered on a theorem about the CCC property (Theorem 1 and Theorem 1a below). So it can be considered as a continuation of a previous post on CCC called Some basic properties of spaces with countable chain condition. The results that are derived from Theorem 1 are also found in [2]. But the theorem concerning CCC is only a small part of that paper among several other focuses. In this post, the exposition is to explain several interesting theorems that are derived from Theorem 1. One of the theorems is the statement that every locally compact metacompact perfectly normal space is paracompact, a theorem originally proved by Arhangelskii (see Theorem 11 below).
____________________________________________________________________
CCC Spaces
All spaces under consideration are at least  and regular. A space
and regular. A space  is said to have the countable chain condition (to have the CCC for short) if
is said to have the countable chain condition (to have the CCC for short) if  is a disjoint collection of non-empty open subsets of
is a disjoint collection of non-empty open subsets of  (meaning that for any
(meaning that for any 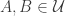 with
with  , we have
, we have 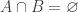 ), then
), then  is countable. In other words, in a space with the CCC, there cannot be uncountably many pairwise disjoint non-empty open sets. For ease of making a statement or stating a result, if
is countable. In other words, in a space with the CCC, there cannot be uncountably many pairwise disjoint non-empty open sets. For ease of making a statement or stating a result, if  has the CCC, we also say that
has the CCC, we also say that  is a CCC space or
is a CCC space or  is CCC.
is CCC.
____________________________________________________________________
A Theorem about CCC Spaces
The theorem of CCC spaces we want to discuss has to do with collections of open sets that are “nice”. We first define what we mean by nice. Let  be a collection of non-empty subsets of the space
be a collection of non-empty subsets of the space  . The collection
. The collection  is said to be point-finite (point-countable) if each point of
is said to be point-finite (point-countable) if each point of  belongs to only finitely (countably) many sets in
belongs to only finitely (countably) many sets in  .
.
Now we define what we mean by “nice” collection of open sets. The collection  is said to be locally finite (locally countable) at a point
is said to be locally finite (locally countable) at a point 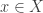 if there exists an open set
if there exists an open set 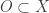 with
with  such that
such that 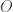 meets at most finitely (countably) many sets in
meets at most finitely (countably) many sets in  . The collection
. The collection  is said to be locally finite (locally countable) if it is locally finite (locally countable) at each
is said to be locally finite (locally countable) if it is locally finite (locally countable) at each 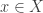 .
.
The property of being a separable space implies the CCC. The reverse is not true. However the CCC property is still a very strong property. The CCC property is equivalent to the property that if a collection of non-empty open sets is “nice” on a dense set of points, then the collection of open sets is a countable collection. The following is a precise statement.
The collections of open sets in the above theorem do not have to be open covers. However, if they are open covers, the theorem can tie CCC spaces with some covering properties. As long as the space has the CCC, any open cover that is locally-countable on a dense set must be countable. Looking at it in the contrapositive angle, in a CCC space, any uncountable open cover is not locally-countable in some open set.
Proof of Theorem 1
Let  be a collection of open subsets of
be a collection of open subsets of  such that the set
such that the set 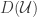 as defined above is dense in the open subspace
as defined above is dense in the open subspace 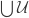 . We show that
. We show that  is countable. Suppose not.
is countable. Suppose not.
For each 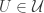 , since
, since 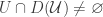 , we can choose a non-empty open set
, we can choose a non-empty open set  such that
such that 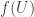 has non-empty intersection with only countably many sets in
has non-empty intersection with only countably many sets in  . Let
. Let 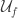 be the following collection:
be the following collection:
For 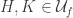 , by a chain from
, by a chain from  to
to  , we mean a finite collection
, we mean a finite collection
such that 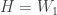 ,
, 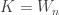 and
and 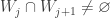 for any
for any 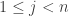 . For each open set
. For each open set 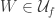 , define
, define  and
and 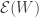 as follows:
as follows:
One observation we make is that for 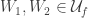 , if
, if 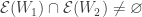 , then
, then  and
and 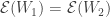 . So the distinct
. So the distinct 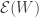 are pairwise disjoint. Because the space
are pairwise disjoint. Because the space  has the CCC, there can be only countably many distinct open sets
has the CCC, there can be only countably many distinct open sets 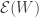 . Thus there can be only countably many distinct collections
. Thus there can be only countably many distinct collections  .
.
Note that each  is a countable collection of open sets. Each
is a countable collection of open sets. Each  meets only countably many open sets in
meets only countably many open sets in  . So each
. So each  can meet only countably many sets in
can meet only countably many sets in 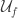 , since for each
, since for each  ,
, 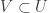 for some
for some 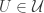 . Thus for each
. Thus for each 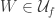 , in considering all finite-length chain starting from
, in considering all finite-length chain starting from  , there can be only countably many open sets in
, there can be only countably many open sets in 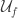 that can be linked to
that can be linked to  . Thus
. Thus  must be countable. In taking the union of all
must be countable. In taking the union of all  , we get back the collection
, we get back the collection 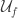 . Thus we have:
. Thus we have:
Because the space  is CCC, there are only countably many distinct collections
is CCC, there are only countably many distinct collections  in the above union. Each
in the above union. Each  is countable. So
is countable. So 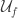 is a countable collection of open sets.
is a countable collection of open sets.
Furthermore, each 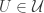 contains at least one set in
contains at least one set in 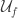 . From the way we choose sets in
. From the way we choose sets in 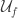 , we see that for each
, we see that for each  ,
, 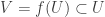 for at most countably many
for at most countably many 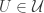 . The argument indicates that we have a one-to-countable mapping from
. The argument indicates that we have a one-to-countable mapping from 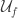 to
to  . Thus the original collection
. Thus the original collection  must be countable.
must be countable. 
The property in Theorem 1 is actually equivalent to the CCC property. Just that the proof of Theorem 1 represents the hard direction that needs to be proved. Theorem 1 can be expanded to be the following theorem.
The direction  has been proved above. The directions
has been proved above. The directions 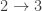 and
and  are straightforward.
are straightforward.
____________________________________________________________________
Tying Theorem 1 to “Nice” Open Covers
One easy application of Theorem 1 is to tie it to locally-finite and locally-countable open covers. We have the following theorem.
Theorem 2
In any CCC space, any locally-countable open cover must be countable. Thus any locally-finite open cover must also be countable.
Theorem 2 gives the well known result that any CCC paracompact space is Lindelof (see Theorem 5 below). In fact, Theorem 2 gives the result that any CCC para-Lindelof space is Lindelof (see Theorem 6 below). A space  is para-Lindelof if every open cover has a locally-countable open refinement.
is para-Lindelof if every open cover has a locally-countable open refinement.
Can Theorem 2 hold for point-finite covers (or point-countable covers)? The answer is no (see Example 1 below). With the additional property of having a Baire space, we have the following theorem.
Theorem 3
In any Baire space with the CCC, any point-finite open cover must be countable.
A Space  is a Baire space if
is a Baire space if 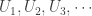 are dense open subsets of
are dense open subsets of  , then
, then 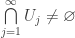 . For more information about Baire spaces, see this previous post.
. For more information about Baire spaces, see this previous post.
.
Proof of Theorem 3
Let  be a Baire space with the CCC. Let
be a Baire space with the CCC. Let  be a point-finite open cover of
be a point-finite open cover of  . Suppose that
. Suppose that  is uncountable. We show that this assumption with lead to a contradiction. Thus
is uncountable. We show that this assumption with lead to a contradiction. Thus  must be countable.
must be countable.
By Theorem 1, there exists an open set 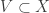 such that
such that  is not locally-countable at any point in
is not locally-countable at any point in  . For each positive integer
. For each positive integer  , let
, let 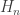 be the following:
be the following:
Note that 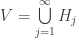 . Furthermore, each
. Furthermore, each 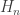 is a closed set in the space
is a closed set in the space  . Since
. Since  is a Baire space, every non-empty open subset of
is a Baire space, every non-empty open subset of  is of second category (i.e. it cannot be a union of countably many closed and nowhere dense sets). Thus it cannot be that each
is of second category (i.e. it cannot be a union of countably many closed and nowhere dense sets). Thus it cannot be that each 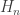 is nowhere dense in
is nowhere dense in  . For some
. For some  ,
, 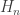 is not nowhere dense. There must exist some open
is not nowhere dense. There must exist some open  such that
such that  is dense in
is dense in  . Because
. Because 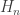 is closed,
is closed,  .
.
Choose  . The point
. The point  is in at most
is in at most  open sets in
open sets in  . Let
. Let 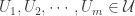 such that
such that 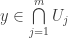 . Clearly
. Clearly 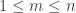 . Let
. Let  . Note that
. Note that  .
.
Every point in  belongs to at most
belongs to at most  many sets in
many sets in  and already belong to
and already belong to  sets in
sets in  . So each point in
. So each point in  can belong to at most
can belong to at most 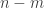 additional open sets in
additional open sets in  . Consider the case
. Consider the case 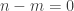 and the case
and the case 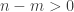 . We show that each case leads to a contradiction.
. We show that each case leads to a contradiction.
Suppose that 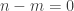 . Then each point of
. Then each point of  can only meet
can only meet  open sets in
open sets in  , namely
, namely 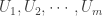 . This contradicts that
. This contradicts that  is not locally-countable at points in
is not locally-countable at points in  .
.
Suppose that 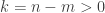 . Let
. Let  . Let
. Let 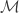 be the following collection:
be the following collection:
Each element of 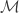 is an open subset of
is an open subset of  that is the intersection of exactly
that is the intersection of exactly  many open sets in
many open sets in  . So
. So 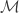 is a collection of pairwise disjoint open sets. The open set
is a collection of pairwise disjoint open sets. The open set  as a topological space has the CCC. So
as a topological space has the CCC. So 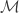 is at most countable. Thus the open set
is at most countable. Thus the open set  meets at most countably many open sets in
meets at most countably many open sets in  , contradicting that
, contradicting that  is not locally-countable at points in
is not locally-countable at points in  .
.
Both cases 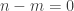 and
and 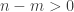 lead to contradiction. So
lead to contradiction. So  must be countable. The proof to Theorem 3 is completed.
must be countable. The proof to Theorem 3 is completed. 
As a corollary to Theorem 3, we have the result that every Baire CCC metacompact space is Lindelof.
____________________________________________________________________
Some Applications of Theorems 2 and 3
In proving paracompactness in some of the theorems, we need a theorem involving the concept of star-countable open cover. A collection  of subsets of a space
of subsets of a space  is said to be star-finite (star-countable) if for each
is said to be star-finite (star-countable) if for each 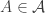 , only finitely (countably) many sets in
, only finitely (countably) many sets in  meets
meets  , i.e., the following set
, i.e., the following set
is finite (countable). The proof of the following theorem can be found in Engleking (see the direction (iv) implies (i) in the proof of Theorem 5.3.10 on page 326 in [1]).
Theorem 4
If every open cover of a regular space  has a star-countable open refinement, then
has a star-countable open refinement, then  is paracompact.
is paracompact.
As indicated in the above section, Theorem 2 and Theorem 3 have some obvious applications. We have the following theorems.
Theorem 5
Let  be a CCC space. Then
be a CCC space. Then  is paracompact if and only of
is paracompact if and only of  is Lindelof.
is Lindelof.
Proof of Theorem 5
The direction  follows from the fact that any regular Lindelof space is paracompact.
follows from the fact that any regular Lindelof space is paracompact.
The direction 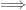 follows from Theorem 2.
follows from Theorem 2. 
Theorem 6
Every CCC para-Lindelof space is Lindelof.
Proof of Theorem 6
This also follows from Theorem 2. 
Theorem 7
Every Baire CCC metacompact space is Lindelof.
Proof of Theorem 7
Let  be a Baire CCC metacompact space. Let
be a Baire CCC metacompact space. Let  be an open cover of
be an open cover of  . By metacompactness, let
. By metacompactness, let  be a point-finite open refinement of
be a point-finite open refinement of  . By Theorem 3,
. By Theorem 3,  must be countable.
must be countable. 
Theorem 8
Every Baire CCC hereditarily metacompact space is hereditarily Lindelof.
Proof of Theorem 8
Let  be a Baire CCC hereditarily metacompact space. To show that
be a Baire CCC hereditarily metacompact space. To show that  is hereditarily Lindelof, it suffices to show that every non-empty open subset is Lindelof. Let
is hereditarily Lindelof, it suffices to show that every non-empty open subset is Lindelof. Let 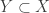 be open. Then
be open. Then  has the CCC and is also metacompact. Being a Baire space is hereditary with respect to open subspaces. So
has the CCC and is also metacompact. Being a Baire space is hereditary with respect to open subspaces. So  is a Baire space too. By Theorem 7,
is a Baire space too. By Theorem 7,  is Lindelof.
is Lindelof. 
Theorem 9
Every locally CCC regular para-Lindelof space is paracompact.
Proof of Theorem 9
A space is locally CCC if every point has an open neighborhood that has the CCC. Let  be a regular space that is locally CCC and para-Lindelof. Let
be a regular space that is locally CCC and para-Lindelof. Let  be an open cover of
be an open cover of  . Using the locally CCC assumption and by taking a refinement of
. Using the locally CCC assumption and by taking a refinement of  if necessary, we can assume that each open set in
if necessary, we can assume that each open set in  has the CCC. By the para-Lindelof assumption, let
has the CCC. By the para-Lindelof assumption, let  be a locally-countable open refinement of
be a locally-countable open refinement of  . So each open set in
. So each open set in  has the CCC too.
has the CCC too.
Now we show that  is star-countable. Let
is star-countable. Let  . Let
. Let  be the following collection:
be the following collection:
which is is open cover of  . Within the subspace
. Within the subspace  ,
,  is a locally-countable open cover. By Theorem 2,
is a locally-countable open cover. By Theorem 2,  must be countable. The collection
must be countable. The collection  represents all the open sets in
represents all the open sets in  that have non-empty intersection with
that have non-empty intersection with  . Thus only countably many open sets in
. Thus only countably many open sets in  can meet
can meet  . So
. So  is a star-countable open refinement of
is a star-countable open refinement of  . By Theorem 4,
. By Theorem 4,  is paracompact.
is paracompact. 
Theorem 10
Every locally CCC regular metacompact Baire space is paracompact.
Proof of Theorem 10
Let  be a regular space that is locally CCC and is a metacompact Baire space. Let
be a regular space that is locally CCC and is a metacompact Baire space. Let  be an open cover of
be an open cover of  . Using the locally CCC assumption and by taking a refinement of
. Using the locally CCC assumption and by taking a refinement of  if necessary, we can assume that each open set in
if necessary, we can assume that each open set in  has the CCC. By the metacompact assumption, let
has the CCC. By the metacompact assumption, let  be a point-finite open refinement of
be a point-finite open refinement of  . So each open set in
. So each open set in  has the CCC too. Each open set in
has the CCC too. Each open set in  is also a Baire space.
is also a Baire space.
Now we show that  is star-countable. Let
is star-countable. Let  . Let
. Let  be the following collection:
be the following collection:
which is is open cover of  . Within the subspace
. Within the subspace  ,
,  is a point-finite open cover. By Theorem 3,
is a point-finite open cover. By Theorem 3,  must be countable. The collection
must be countable. The collection  represents all the open sets in
represents all the open sets in  that have non-empty intersection with
that have non-empty intersection with  . Thus only countably many open sets in
. Thus only countably many open sets in  can meet
can meet  . So
. So  is a star-countable open refinement of
is a star-countable open refinement of  . By Theorem 4,
. By Theorem 4,  is paracompact.
is paracompact. 
Theorem 11
Every locally compact metacompact perfectly normal space is paracompact.
Proof of Theorem 11
This follows from Theorem 10 after we prove the following two points:
- Any locally compact space is a Baire space.
- Any perfect locally compact space is locally CCC.
To see the first point, let  be a locally compact space. Let
be a locally compact space. Let 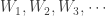 be dense open sets in
be dense open sets in  . Let
. Let 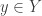 and let
and let 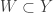 be open such that
be open such that  and
and  is compact. We show that
is compact. We show that  contains a point that belongs to all
contains a point that belongs to all  . Let
. Let 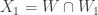 , which is open and non-empty. Next choose non-empty open
, which is open and non-empty. Next choose non-empty open 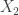 such that
such that  and
and 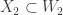 . Next choose non-empty open
. Next choose non-empty open 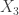 such that
such that  and
and  . Continue in this manner, we have a sequence of open sets
. Continue in this manner, we have a sequence of open sets  such that for each
such that for each  ,
, 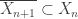 and
and  is compact. The intersection of all the
is compact. The intersection of all the 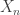 is non-empty. The points in the intersection must belong to each
is non-empty. The points in the intersection must belong to each  .
.
To see the second point, let  be a locally compact space such that every closed set is a
be a locally compact space such that every closed set is a  -set. Suppose that
-set. Suppose that  is not locally CCC at
is not locally CCC at 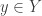 . Let
. Let 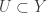 be open such that
be open such that 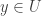 and
and 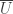 is compact. Then
is compact. Then  must not have the CCC. Let
must not have the CCC. Let 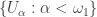 be a pairwise disjoint collection of open subsets of
be a pairwise disjoint collection of open subsets of  . Let
. Let  and let
and let 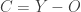 .
.
Let  where each
where each 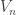 is open in
is open in  and
and 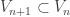 for each integer
for each integer  . For each
. For each  , pick
, pick 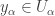 . For each
. For each 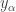 , there is some integer
, there is some integer 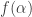 such that
such that 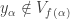 . So there must exist some integer
. So there must exist some integer  such that
such that 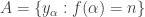 is uncountable.
is uncountable.
The set  is an infinite subset of the compact set
is an infinite subset of the compact set 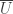 . So
. So  has a limit point, say
has a limit point, say  (also called cluster point). Clearly
(also called cluster point). Clearly 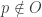 . So
. So 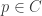 . In particular,
. In particular, 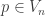 . Then
. Then 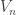 contains some points of
contains some points of  . But for any
. But for any  ,
,  , a contradiction. So
, a contradiction. So  must be locally CCC at each
must be locally CCC at each 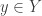 .
. 
____________________________________________________________________
Some Examples
Example 1
A CCC space  with an uncountable point-finite open covers. This example demonstrates that in Theorem 2, locally-finite or locally-countable cannot be replaced by point-finite. Consider the following product space:
with an uncountable point-finite open covers. This example demonstrates that in Theorem 2, locally-finite or locally-countable cannot be replaced by point-finite. Consider the following product space:
i.e, the product space of  many copies of the two-point discrete space
many copies of the two-point discrete space 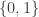 . Let
. Let  be the set of all points
be the set of all points 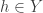 such that
such that 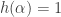 for only finitely many
for only finitely many  .
.
The product space  is the product of separable spaces, hence has the CCC. The space
is the product of separable spaces, hence has the CCC. The space  is dense in
is dense in  . Hence
. Hence  has the CCC. For each
has the CCC. For each  , define
, define 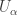 as follows:
as follows:
Then 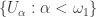 is a point-finite open cover of
is a point-finite open cover of  . Of course,
. Of course,  in this example is not a Baire space.
in this example is not a Baire space. 
The following three examples center around the four properties in Theorem 7 (Baire + CCC + metacompact imply Lindelof). These examples show that each property in the hypothesis is crucial.
Example 2
A separable non-Lindelof space that is a Baire space. This example shows that the metacompact assumption is crucial for Theorem 7.
The example is the Sorgenfrey plane  where
where  is the real line with the Sorgenfrey topology (generated by the half-open intervals of the form
is the real line with the Sorgenfrey topology (generated by the half-open intervals of the form 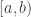 ). It is well known that
). It is well known that  is not Lindelof. The Sorgenfrey plane is Baire and is separable (hence CCC). Furthermore,
is not Lindelof. The Sorgenfrey plane is Baire and is separable (hence CCC). Furthermore,  is not metacompact (if it were, it would be Lindelof by Theorem 7).
is not metacompact (if it were, it would be Lindelof by Theorem 7). 
Example 3
A non-Lindelof metacompact Baire space  . This example shows that the CCC assumption in Theorem 7 is necessary.
. This example shows that the CCC assumption in Theorem 7 is necessary.
This space  is the subspace of Bing’s Example G that has finite support (defined and discussed in the post A subspace of Bing’s example G. It is normal and not collectionwise normal (hence cannot be Lindelof) and metacompact. The space
is the subspace of Bing’s Example G that has finite support (defined and discussed in the post A subspace of Bing’s example G. It is normal and not collectionwise normal (hence cannot be Lindelof) and metacompact. The space  does not have CCC since it has uncountably many isolated points. Any space with a dense set of isolated points is a Baire space. Thus the space
does not have CCC since it has uncountably many isolated points. Any space with a dense set of isolated points is a Baire space. Thus the space  is also a Baire space.
is also a Baire space. 
Example 4
A non-Lindelof CCC metacompact non-Baire space  . This example shows that the Baire space assumption in Theorem 7 is necessary.
. This example shows that the Baire space assumption in Theorem 7 is necessary.
Let  be the set of all non-empty finite subsets of the real line with the Pixley-Roy topology. Note that
be the set of all non-empty finite subsets of the real line with the Pixley-Roy topology. Note that  is non-Lindelof and has the CCC and is metacompact. Of course it is not Baire. For more information on Pixley-Roy spaces, see the post called Pixley-Roy hyperspaces. For the purpose of this example, the Pixley-Roy space can be built on any uncountable separable metrizable space.
is non-Lindelof and has the CCC and is metacompact. Of course it is not Baire. For more information on Pixley-Roy spaces, see the post called Pixley-Roy hyperspaces. For the purpose of this example, the Pixley-Roy space can be built on any uncountable separable metrizable space.
____________________________________________________________________
Reference
- Engelking, R., General Topology, Revised and Completed edition, Heldermann Verlag, Berlin, 1989.
- Tall, F. D., The Countable Chain Condition Versus Separability – Applications of Martin’s Axiom, Gen. Top. Appl., 4, 315-339, 1974.
____________________________________________________________________

be a mapping from a topological space
onto a topological space
. If
is a perfect map and
is a Lindelof space, then so is
. If
is a closed map and
is a paracompact space, then so is
. In other words, the pre-image of a Lindelof space under a perfect map is always a Lindelof space. Likewise, the pre-image of a paracompact space under a closed map is always a paracompact space. After proving these two facts, we show that for any compact space
, the product
is Lindelof (paracompact) for any Lindelof (paracompact) space
. All spaces under consideration are Hausdorff.
if the following holds: for any mapping
belonging to
, if
has the property, then so does
. In contrast, a topological property is an invariance of a class of mappings
if for any mapping
belonging to
, if
has the property, then so does
.
, where
, is a closed map if for any closed subset
of
,
is closed in
. A mapping
, where
, is a perfect map if
is a closed map and that the point inverse
is compact for each
.
be a closed map with
. Let
be an open subset of
. Define
. Then the set
is open in
and that
.
be a perfect map with
. Suppose
is Lindelof. Let
be an open cover of
. Without loss of generality, we can assume that
is closed under finite unions. For each
, define
. By Lemma 3, each
is an open subset of
. We claim that
is an open cover of
. To this end, let
. Since
is a perfect map, the point inverse
is compact. As a result, we can find a finite
such that
. Since
is closed under finite unions,
. It follows that
. Since
is Lindelof, there exists a countable
such that
. For each
,
for some
. We claim that
is a cover of
. To this end, let
. Then for some
,
. This implies that
. Thus, the open cover
has a countable subcover. This concludes the proof of Theorem 1.
be a perfect map with
. Suppose
is paracompact. Let
be an open cover of
. For each
, define
as in Lemma 3. By Lemma 3, each
is an open subset of
. Let
. As shown in the proof of Theorem 1,
is an open cover of
. Since
is paracompact, there exists a locally finite open refinement
of
. Let
.
. (1) It is an open cover of
. (2) It is a locally finite collection in
. (3) It is a refinement of
. To see (1), note that
is an open cover of
. As a result,
is an open cover of
. To see (2), let
. We find an open
such that
and such that
intersects only finitely many elements of
. Since
is locally finite in
, there exists an open
such that
and such that
intersects only finitely many elements of
, say,
. Let
. Clearly,
. It can be verified that the only elements of
having non-empty intersections with
are
,
,
. To see (3), let
where
. Then
for some
and some
. We claim that
. Let
. Then
. This implies that
. It follows that
is a locally finite open refinement of the open cover
. This completes the proof of Theorem 2.
is productively paramcompact if
is paracompact for every paracompact space
. The definition for productively Lindelof can be stated in a similar way. For some reason, the term “productively paracompact” is not used in the literature but is a topic that had been extensively studied. It is also a topic found in this site. The following four classes of spaces are productively paracompact (see here and here).
-compact spaces
-locally compact spaces
any compact space. Then
is Lindelof for every Lindelof space
.
any compact space. Then
is paracompact for every paracompact space
.
is compact. Then the projection map from
onto
is a closed map. The paracompactness of
follows whenever
is paracompact. The projection map is also perfect since the point inverses are compact due to the compactness of the factor
. Then the Lindelofness of
follows whenever
is Lindelof.
2023 – Dan Ma
