Like the Sorgenfrey line, the Michael line is a classic counterexample that is covered in standard topology textbooks and in first year topology courses. This easily accessible example helps transition students from the familiar setting of the Euclidean topology on the real line to more abstract topological spaces. One of the most famous results regarding the Michael line is that the product of the Michael line with the space of the irrational numbers is not normal. Thus it is an important example in demonstrating the pathology in products of paracompact spaces. The product of two paracompact spaces does not even have be to be normal, even when one of the factors is a complete metric space. In this post, we discuss this classical result and various other basic results of the Michael line.
Let  be the real number line. Let
be the real number line. Let  be the set of all irrational numbers. Let
be the set of all irrational numbers. Let  , the set of all rational numbers. Let
, the set of all rational numbers. Let  be the usual topology of the real line
be the usual topology of the real line  . The following is a base that defines a topology on
. The following is a base that defines a topology on  .
.
The real line with the topology generated by  is called the Michael line and is denoted by
is called the Michael line and is denoted by  . In essense, in
. In essense, in  , points in
, points in  are made isolated and points in
are made isolated and points in 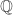 retain the usual Euclidean open sets.
retain the usual Euclidean open sets.
The Euclidean topology  is coarser (weaker) than the Michael line topology (i.e.
is coarser (weaker) than the Michael line topology (i.e.  being a subset of the Michael line topology). Thus the Michael line is Hausdorff. Since the Michael line topology contains a metrizable topology,
being a subset of the Michael line topology). Thus the Michael line is Hausdorff. Since the Michael line topology contains a metrizable topology,  is submetrizable (submetrized by the Euclidean topology). It is clear that
is submetrizable (submetrized by the Euclidean topology). It is clear that  is first countable. Having uncountably many isolated points, the Michael line does not have the countable chain condition (thus is not separable). The following points are discussed in more details.
is first countable. Having uncountably many isolated points, the Michael line does not have the countable chain condition (thus is not separable). The following points are discussed in more details.
- The space
 is paracompact.
is paracompact.
- The space
 is not Lindelof.
is not Lindelof.
- The extent of the space
 is
is  where
where  is the cardinality of the real line.
is the cardinality of the real line.
- The space
 is not locally compact.
is not locally compact.
- The space
 is not perfectly normal, thus not metrizable.
is not perfectly normal, thus not metrizable.
- The space
 is not a Moore space, but has a
is not a Moore space, but has a  -diagonal.
-diagonal.
- The product
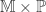 is not normal where
is not normal where  has the usual topology.
has the usual topology.
- The product
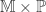 is metacompact.
is metacompact.
- The space
 has a point-countable base.
has a point-countable base.
- For each
 , the product
, the product 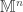 is paracompact.
is paracompact.
- The product
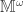 is not normal.
is not normal.
- There exist a Lindelof space
 and a separable metric space
and a separable metric space  such that
such that 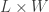 is not normal.
is not normal.
Results 10, 11 and 12 are shown in some subsequent posts.
___________________________________________________________________________________
Baire Category Theorem
Before discussing the Michael line in greater details, we point out one connection between the Michael line topology and the Euclidean topology on the real line. The Michael line topology on 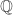 coincides with the Euclidean topology on
coincides with the Euclidean topology on 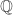 . A set is said to be a
. A set is said to be a  -set if it is the intersection of countably many open sets. By the Baire category theorem, the set
-set if it is the intersection of countably many open sets. By the Baire category theorem, the set 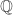 is not a
is not a  -set in the Euclidean real line (see the section called “Discussion of the Above Question” in the post A Question About The Rational Numbers). Thus the set
-set in the Euclidean real line (see the section called “Discussion of the Above Question” in the post A Question About The Rational Numbers). Thus the set 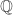 is not a
is not a  -set in the Michael line. This fact is used in Result 5.
-set in the Michael line. This fact is used in Result 5.
The fact that 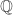 is not a
is not a  -set in the Euclidean real line implies that
-set in the Euclidean real line implies that  is not an
is not an 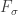 -set in the Euclidean real line. This fact is used in Result 7.
-set in the Euclidean real line. This fact is used in Result 7.
___________________________________________________________________________________
Result 1
Let  be an open cover of
be an open cover of  . We proceed to derive a locally finite open refinement
. We proceed to derive a locally finite open refinement  of
of  . Recall that
. Recall that  is the usual topology on
is the usual topology on  . Assume that
. Assume that  consists of open sets in the base
consists of open sets in the base  . Let
. Let 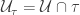 . Let
. Let  . Note that
. Note that  is a Euclidean open subspace of the real line (hence it is paracompact). Then there is
is a Euclidean open subspace of the real line (hence it is paracompact). Then there is  such that
such that  is a locally finite open refinement
is a locally finite open refinement  of
of  and such that
and such that  covers
covers  (locally finite in the Euclidean sense). Then add to
(locally finite in the Euclidean sense). Then add to  all singleton sets
all singleton sets 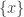 where
where 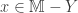 and let
and let  denote the resulting open collection.
denote the resulting open collection.
The resulting  is a locally finite open collection in the Michael line
is a locally finite open collection in the Michael line  . Furthermore,
. Furthermore,  is also a refinement of the original open cover
is also a refinement of the original open cover  .
. 
A similar argument shows that  is hereditarily paracompact.
is hereditarily paracompact.
___________________________________________________________________________________
Result 2
To see that  is not Lindelof, observe that there exist Euclidean uncountable closed sets consisting entirely of irrational numbers (i.e. points in
is not Lindelof, observe that there exist Euclidean uncountable closed sets consisting entirely of irrational numbers (i.e. points in  ). For example, it is possible to construct a Cantor set entirely within
). For example, it is possible to construct a Cantor set entirely within  .
.
Let  be an uncountable Euclidean closed set consisting entirely of irrational numbers. Then this set
be an uncountable Euclidean closed set consisting entirely of irrational numbers. Then this set  is an uncountable closed and discrete set in
is an uncountable closed and discrete set in  . In any Lindelof space, there exists no uncountable closed and discrete subset. Thus the Michael line
. In any Lindelof space, there exists no uncountable closed and discrete subset. Thus the Michael line  cannot be Lindelof.
cannot be Lindelof. 
___________________________________________________________________________________
Result 3
The argument in Result 2 indicates a more general result. First, a brief discussion of the cardinal function extent. The extent of a space  is the smallest infinite cardinal number
is the smallest infinite cardinal number 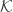 such that every closed and discrete set in
such that every closed and discrete set in  has cardinality
has cardinality 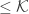 . The extent of the space
. The extent of the space  is denoted by
is denoted by 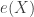 . When the cardinal number
. When the cardinal number 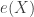 is
is 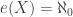 (the first infinite cardinal number), the space
(the first infinite cardinal number), the space  is said to have countable extent, meaning that in this space any closed and discrete set must be countably infinite or finite. When
is said to have countable extent, meaning that in this space any closed and discrete set must be countably infinite or finite. When 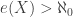 , there are uncountable closed and discrete subsets in the space.
, there are uncountable closed and discrete subsets in the space.
It is straightforward to see that if a space  is Lindelof, the extent is
is Lindelof, the extent is 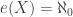 . However, the converse is not true.
. However, the converse is not true.
The argument in Result 2 exhibits a closed and discrete subset of  of cardinality
of cardinality  . Thus we have
. Thus we have 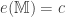 .
. 
___________________________________________________________________________________
Result 4
The Michael line  is not locally compact at all rational numbers. Observe that the Michael line closure of any Euclidean open interval is not compact in
is not locally compact at all rational numbers. Observe that the Michael line closure of any Euclidean open interval is not compact in  .
. 
___________________________________________________________________________________
Result 5
A set is said to be a  -set if it is the intersection of countably many open sets. A space is perfectly normal if it is a normal space with the additional property that every closed set is a
-set if it is the intersection of countably many open sets. A space is perfectly normal if it is a normal space with the additional property that every closed set is a  -set. In the Michael line
-set. In the Michael line  , the set
, the set 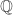 of rational numbers is a closed set. Yet,
of rational numbers is a closed set. Yet, 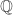 is not a
is not a  -set in the Michael line (see the discussion above on the Baire category theorem). Thus
-set in the Michael line (see the discussion above on the Baire category theorem). Thus  is not perfectly normal and hence not a metrizable space.
is not perfectly normal and hence not a metrizable space. 
___________________________________________________________________________________
Result 6
The diagonal of a space  is the subset of its square
is the subset of its square 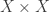 that is defined by
that is defined by 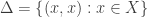 . If the space is Hausdorff, the diagonal is always a closed set in the square. If
. If the space is Hausdorff, the diagonal is always a closed set in the square. If  is a
is a  -set in
-set in 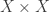 , the space
, the space  is said to have a
is said to have a  -diagonal. It is well known that any metric space has
-diagonal. It is well known that any metric space has  -diagonal. Since
-diagonal. Since  is submetrizable (submetrized by the usual topology of the real line), it has a
is submetrizable (submetrized by the usual topology of the real line), it has a  -diagonal too.
-diagonal too.
Any Moore space has a  -diagonal. However, the Michael line is an example of a space with
-diagonal. However, the Michael line is an example of a space with  -diagonal but is not a Moore space. Paracompact Moore spaces are metrizable. Thus
-diagonal but is not a Moore space. Paracompact Moore spaces are metrizable. Thus  is not a Moore space. For a more detailed discussion about Moore spaces, see Sorgenfrey Line is not a Moore Space.
is not a Moore space. For a more detailed discussion about Moore spaces, see Sorgenfrey Line is not a Moore Space. 
___________________________________________________________________________________
Result 7
We now show that 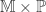 is not normal where
is not normal where  has the usual topology. In this proof, the following two facts are crucial:
has the usual topology. In this proof, the following two facts are crucial:
- The set
 is not an
is not an 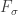 -set in the real line.
-set in the real line.
- The set
 is dense in the real line.
is dense in the real line.
Let  and
and  be defined by the following:
be defined by the following:
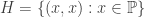
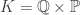 .
.
The sets  and
and  are disjoint closed sets in
are disjoint closed sets in 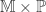 . We show that they cannot be separated by disjoint open sets. To this end, let
. We show that they cannot be separated by disjoint open sets. To this end, let  and
and  where
where  and
and  are open sets in
are open sets in 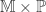 .
.
To make the notation easier, for the remainder of the proof of Result 7, by an open interval 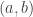 , we mean the set of all real numbers
, we mean the set of all real numbers  with
with 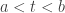 . By
. By  , we mean
, we mean  . For each
. For each 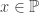 , choose an open interval
, choose an open interval  such that
such that 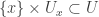 . We also assume that
. We also assume that  is the midpoint of the open interval
is the midpoint of the open interval 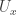 . For each positive integer
. For each positive integer  , let
, let 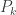 be defined by:
be defined by:
Note that  . For each
. For each  , let
, let 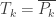 (Euclidean closure in the real line). It is clear that
(Euclidean closure in the real line). It is clear that 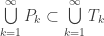 . On the other hand,
. On the other hand, 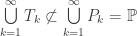 (otherwise
(otherwise  would be an
would be an 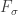 -set in the real line). So there exists
-set in the real line). So there exists 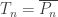 such that
such that  . So choose a rational number
. So choose a rational number  such that
such that 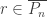 .
.
Choose a positive integer  such that
such that 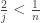 . Since
. Since  is dense in the real line, choose
is dense in the real line, choose  such that
such that 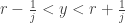 . Now we have
. Now we have 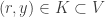 . Choose another integer
. Choose another integer  such that
such that  and
and  .
.
Since 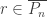 , choose
, choose 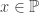 such that
such that  . Now it is clear that
. Now it is clear that 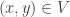 . The following inequalities show that
. The following inequalities show that 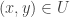 .
.
The open interval 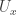 is chosen to have length
is chosen to have length 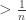 . Since
. Since  ,
, 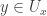 . Thus
. Thus 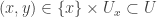 . We have shown that
. We have shown that  . Thus
. Thus 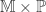 is not normal.
is not normal. 
Remark
As indicated above, the proof of Result 7 hinges on two facts about  , namely that it is not an
, namely that it is not an 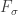 -set in the real line and it is dense in the real line. We can modify the construction of the Michael line by using other partition of the real line (where one set is isolated and its complement retains the usual topology). As long as the set
-set in the real line and it is dense in the real line. We can modify the construction of the Michael line by using other partition of the real line (where one set is isolated and its complement retains the usual topology). As long as the set  that is isolated is not an
that is isolated is not an 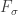 -set in the real line and is dense in the real line, the same proof will show that the product of the modified Michael line and the space
-set in the real line and is dense in the real line, the same proof will show that the product of the modified Michael line and the space  (with the usual topology) is not normal. This will be how Result 12 is derived.
(with the usual topology) is not normal. This will be how Result 12 is derived.
___________________________________________________________________________________
Result 8
The product 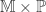 is not paracompact since it is not normal. However,
is not paracompact since it is not normal. However, 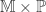 is metacompact.
is metacompact.
A collection of subsets of a space  is said to be point-finite if every point of
is said to be point-finite if every point of  belongs to only finitely many sets in the collection. A space
belongs to only finitely many sets in the collection. A space  is said to be metacompact if each open cover of
is said to be metacompact if each open cover of  has an open refinement that is a point-finite collection.
has an open refinement that is a point-finite collection.
Note that 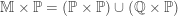 . The first
. The first  in
in 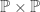 is discrete (a subspace of the Michael line) and the second
is discrete (a subspace of the Michael line) and the second  has the Euclidean topology.
has the Euclidean topology.
Let  be an open cover of
be an open cover of 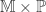 . For each
. For each 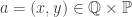 , choose
, choose  such that
such that 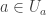 . We can assume that
. We can assume that 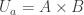 where
where  is a usual open interval in
is a usual open interval in  and
and  is a usual open interval in
is a usual open interval in  . Let
. Let 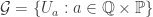 .
.
Fix 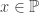 . For each
. For each 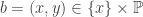 , choose some
, choose some  such that
such that  . We can assume that
. We can assume that 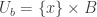 where
where  is a usual open interval in
is a usual open interval in  . Let
. Let 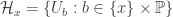 .
.
As a subspace of the Euclidean plane,  is metacompact. So there is a point-finite open refinement
is metacompact. So there is a point-finite open refinement 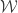 of
of  . For each
. For each 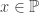 ,
, 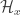 has a point-finite open refinement
has a point-finite open refinement  . Let
. Let  be the union of
be the union of 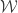 and all the
and all the  where
where 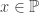 . Then
. Then  is a point-finite open refinement of
is a point-finite open refinement of  .
.
Note that the point-finite open refinement  may not be locally finite. The vertical open intervals in
may not be locally finite. The vertical open intervals in 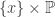 ,
, 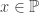 can “converge” to a point in
can “converge” to a point in 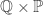 . Thus, metacompactness is the best we can hope for.
. Thus, metacompactness is the best we can hope for. 
___________________________________________________________________________________
Result 9
A collection of sets is said to be point-countable if every point in the space belongs to at most countably many sets in the collection. A base  for a space
for a space  is said to be a point-countable base if
is said to be a point-countable base if  , in addition to being a base for the space
, in addition to being a base for the space  , is also a point-countable collection of sets. The Michael line is an example of a space that has a point-countable base and that is not metrizable. The following is a point-countable base for
, is also a point-countable collection of sets. The Michael line is an example of a space that has a point-countable base and that is not metrizable. The following is a point-countable base for  :
:
where 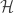 is the set of all Euclidean open intervals with rational endpoints. One reason for the interest in point-countable base is that any countable compact space (hence any compact space) with a point-countable base is metrizable (see Metrization Theorems for Compact Spaces).
is the set of all Euclidean open intervals with rational endpoints. One reason for the interest in point-countable base is that any countable compact space (hence any compact space) with a point-countable base is metrizable (see Metrization Theorems for Compact Spaces).
___________________________________________________________________________________
Reference
- Engelking, R., General Topology, Revised and Completed edition, Heldermann Verlag, Berlin, 1989.
- Willard, S., General Topology, Addison-Wesley Publishing Company, 1970.
___________________________________________________________________________________
be a perfect map onto the space
. Then
, i.e., the weight of
is no greater than the weight of
.
and
be spaces. Let
be a map (or function) from
onto
. The map
is said to be a closed map if
is closed in
for any closed subset
of
. The map
is a perfect map if
is continuous,
is a closed map, and
is compact for every
. In words, the last condition is that every point inverse is compact. A point inverse
is also referred to as a fiber. Thus, we can say that a perfect map is a continuous closed surjective map with compact fibers. The following lemma is helpful for proving Theorem 1.
be a closed map such that
. Let
be open. Let
. Then
is open in
and
.
is closed in
. To this end, we show
. Note that
is closed in
since
is a closed map. First, we show
. Let
. Then
for some
. Since
and
, we have
. This implies that
.
. Let
. Since
,
. Choose
, which implies that
. Thus,
.
. Let
. We have
. As a result,
for some
.
be a base for
. We derive a base
for
such that
, i.e., the cardinality of
is no more than the cardinality of
. This implies that the minimal cardinality of a base in
is no more than the minimal cardinality of a base in
, i.e.,
.
is closed under finite unions. We show that
is a base for
. Note that
is defined in Lemma 2. Let
be an open set. Let
. For each
, choose
such that
and
. Since
is compact, there exists finite
such that
. Note that
. Since
, we have
. We also have
. Thus, every open subset
of
is the union of elements of
. This means that
is a base for
. Theorem 1 is established.
be a perfect map onto the space
. Then if
is a separable metric space, then
is a separable metric space.
in Theorem 1 is an open map, then Lemma 2 is not needed and
would be a base for
. However, we cannot assume
is an open map simply because it is a perfect map. To see this, let
be the real line with the usual topology. Collapse the closed interval
to one point called
. The resulting quotient space is
where
. In
, the open neighborhoods of points in
are the usual Euclidean neighborhoods. The open neighborhoods of the point
are the usual Euclidean open sets containing the interval
. The resulting quotient map
is an identity map on
and it maps points in
to the point
. It can be verified that
is a perfect map. For the open set
,
, which is not open in
. For the open set
,
, which is not open in
. Lemma 2 says that for any open
,
may not be open but has an open subset
if
has non-empty interior. The interior sets
can work as a base in
.
be a property of topological spaces. We say that
is an invariant of the perfect maps or that
is invariant under the perfect maps if the property
is preserved by perfect maps, i.e., for each perfect map
where
, if the space
has
, so does
. On the other hand,
is an inverse invariant of the perfect maps if this holds: for each perfect map
where
, if
has
, so does
.
” is an invariant of the perfect maps.
2023 – Dan Ma

