Drawing Sorgenfrey continuous functions

Posted on September 5, 2017 by Dan Ma

The Sorgenfrey line is a well known topological space. It is the real number line with open intervals defined as sets of the form $[a,b)$ . Though this is a seemingly small tweak, it generates a vastly different space than the usual real number line. In this post, we look at the Sorgenfrey line from the continuous function perspective, in particular, the continuous functions that map the Sorgenfrey line into the real number line. In the process, we obtain insight into the space of continuous functions on the Sorgenfrey line.

The next post is a continuation on the theme of drawing Sorgenfrey continuous functions.

The Sorgenfrey Line

Let $\mathbb{R}$ denote the real number line. The usual open intervals are of the form $(a,b)=\left\{x \in \mathbb{R}: a<x<b \right\}$ . The union of such open intervals is called an open set. If more than one topologies are considered on the real line, these open sets are referred to as the usual open sets or Euclidean open sets (on the real line). The open intervals $(a,b)$ form a base for the usual topology on the real line. One important fact abut the usual open sets is that the usual open sets can be generated by the intervals $(a,b)$ where both end points are rational numbers. Thus the usual topology on the real line is said to have a countable base.

Now tweak the usual topology by calling sets of the form $[a,b)=\left\{x \in \mathbb{R}: a \le x<b \right\}$ open intervals. Then form open sets by taking unions of all such open intervals. The collection of such open sets is called the Sorgenfrey topology (on the real line). The real number line $\mathbb{R}$ with the Sorgenfry topology is called the Sorgenfrey line, denoted by $\mathbb{S}$ . The Sorgenfrey line has been discussed in this blog, starting with this post. This post examines continuous functions from $\mathbb{S}$ into the real line. In the process, we gain insight on the space of continuous functions defined on $\mathbb{S}$ .

Note that any usual open interval $(a,b)$ is the union of intervals of the form $[c,d)$ . Thus any usual (Euclidean) open set is an open set in the Sorgenfrey line. Thus the usual topology (on the real line) is contained in the Sorgenfrey topology, i.e. the usual topology is a weaker (coarser) topology.

Let $C(\mathbb{R})$ be the set of all continuous functions $f:\mathbb{R} \rightarrow \mathbb{R}$ where the domain is the real number line with the usual topology. Let $C(\mathbb{S})$ be the set of all continuous functions $f:\mathbb{S} \rightarrow \mathbb{R}$ where the domain is the Sorgenfrey line. In both cases, the range is always the number line with the usual topology. Based on the preceding paragraph, any continuous function $f:\mathbb{R} \rightarrow \mathbb{R}$ is also continuous with respect to the Sorgenfrey line, i.e. $C(\mathbb{R}) \subset C(\mathbb{S})$ .

Pictures of Continuous Functions

Consider the following two continuous functions.

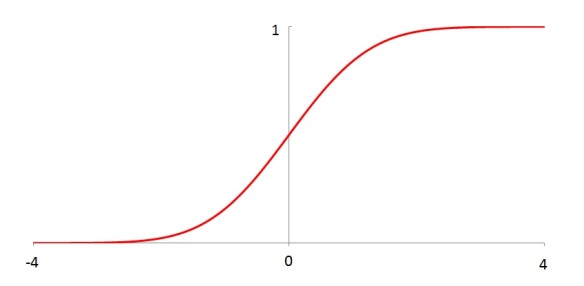
Figure 1 – CDF of the standard normal distribution

Figure 2 – CDF of the uniform distribution

The first one (Figure 1) is the cumulative distribution function (CDF) of the standard normal distribution. The second one (Figure 2) is the CDF of the uniform distribution on the interval $(0,a)$ where $a>0$ . Both of these are continuous in the usual Euclidean topology (in the domain). Such graphs would make regular appearance in a course on probability and statistics. They also show up in a calculus course as an everywhere differentiable curve (Figure 1) and as a differentiable curve except at finitely many points (Figure 2). Both of these functions can also be regarded as continuous functions on the Sorgenfrey line.

Consider a function that is continuous in the Sorgenfrey line but not continuous in the usual topology.

Figure 3 – Right continuous function

Figure 3 is a function that maps the interval $(-\infty,0)$ to -1 and maps the interval $[0,\infty)$ to 1. It is not continuous in the usual topology because of the jump at $x=0$ . But it is a continuous function when the domain is considered to be the Sorgenfrey line. Because of the open intervals being $[a,b)$ , continuous functions defined on the Sorgenfrey line are right continuous.

The cumulative distribution function of a discrete probability distribution is always right continuous, hence continuous in the Sorgenfrey line. Here’s an example.

Figure 4 – CDF of a discrete uniform distribution

Figure 4 is the CDF of the uniform distribution on the finite set $\left\{0,1,2,3,4 \right\}$ , where each point has probability 0.2. There is a jump of height 0.2 at each of the points from 0 to 4. Figure 3 and Figure 4 are step functions. As long as the left point of a step is solid and the right point is hollow, the step functions are continuous on the Sorgenfrey line.

The take away from the last four figures is that the real-valued continuous functions defined on the Sorgenfrey line are right continuous and that step functions (with the left point solid and the right point hollow) are Sorgenfrey continuous.

A Family of Sorgenfrey Continuous Functions

The four examples of continuous functions shown above are excellent examples to illustrate the Sorgenfrey topology. We now introduce a family of continuous functions $f_a:\mathbb{S} \rightarrow \mathbb{R}$ for $0<a<1$ . These continuous functions will lead to additional insight on the function space whose domain space is the Sorgenfrey line.

For any $0<a<1$ , the following gives the definition and the graph of the function $f_a$ .

$\displaystyle f_a(x) = \left\{ \begin{array}{ll} \displaystyle 0 &\ \ \ \ \ \ -\infty<x<-1 \\ \text{ } & \text{ } \\ \displaystyle 1 &\ \ \ \ \ \ -1 \le x<-a \\ \text{ } & \text{ } \\ 0 &\ \ \ \ \ \ -a \le x <a \\ \text{ } & \text{ } \\ 1 &\ \ \ \ \ \ a \le x <1 \\ \text{ } & \text{ } \\ 0 &\ \ \ \ \ \ 1 \le x <\infty \end{array} \right.$

Figure 5 – a family of Sorgenfrey continuous functions

Function Space on the Sorgenfrey Line

This is the place where we switch the focus to function space. The set $C(\mathbb{S})$ is a subset of the product space $\mathbb{R}^\mathbb{R}$ . So we can consider $C(\mathbb{S})$ as a topological space endowed with the topology inherited as a subspace of $\mathbb{R}^\mathbb{R}$ . This topology on $C(\mathbb{S})$ is called the pointwise convergence topology and $C(\mathbb{S})$ with the product subspace topology is denoted by $C_p(\mathbb{S})$ . See here for comments on how to work with the pointwise convergence topology.

For the present discussion, all we need is some notation on a base for $C_p(\mathbb{S})$ . For $x \in \mathbb{S}$ , and for any open interval $(a,b)$ (open in the usual topology of the real number line), let $[x,(a,b)]=\left\{h \in C_p(\mathbb{S}): h(x) \in (a, b) \right\}$ . Then the collection of intersections of finitely many $[x,(a,b)]$ would form a base for $C_p(\mathbb{S})$ .

The following is the main fact we wish to establish.

The function space $C_p(\mathbb{S})$ contains a closed and discrete subspace of cardinality continuum. In particular, the set $F=\left\{f_a: 0<a<1 \right\}$ is a closed and discrete subspace of $C_p(\mathbb{S})$ .

The above result will derive several facts on the function space $C_p(\mathbb{S})$ , which are discussed in a section below. More interestingly, the proof of the fact that $F=\left\{f_a: 0<a<1 \right\}$ is a closed and discrete subspace of $C_p(\mathbb{S})$ is based purely on the definition of the functions $f_a$ and the Sorgenfrey topology. The proof given below does not use any deep or high powered results from function space theory. So it should be a nice exercise on the Sorgenfrey topology.

I invite readers to either verify the fact independently of the proof given here or follow the proof closely. Lots of drawing of the functions $f_a$ on paper will be helpful in going over the proof. In this one instance at least, drawing continuous functions can help gain insight on function spaces.

Working out the Proof

The following diagram was helpful to me as I worked out the different cases in showing the discreteness of the family $F=\left\{f_a: 0<a<1 \right\}$ . The diagram is a valuable aid in convincing myself that a given case is correct.

Figure 6 – A comparison of three Sorgenfrey continuous functions

Now the proof. First, $F$ is relatively discrete in $C_p(\mathbb{S})$ . We show that for each $a$ , there is an open set $O$ containing $f_a$ such that $O$ does not contain $f_w$ for any $w \ne a$ . To this end, let $O=[a,V_1] \cap [-a,V_2]$ where $V_1$ and $V_2$ are the open intervals $V_1=(0.9,1.1)$ and $V_2=(-0.1,0.1)$ . With Figure 6 as an aid, it follows that for $0<b<a$ , $f_b \notin O$ and for $a<c<1$ , $f_c \notin O$ .

The open set $O=[a,V_1] \cap [-a,V_2]$ contains $f_a$ , the function in the middle of Figure 6. Note that for $0<b<a$ , $f_b(-a)=1$ and $f_b(-a) \notin V_2$ . Thus $f_b \notin O$ . On the other hand, for $a<c<1$ , $f_c(a)=0$ and $f_c(a) \notin V_1$ . Thus $f_c \notin O$ . This proves that the set $F$ is a discrete subspace of $C_p(\mathbb{S})$ relative to $F$ itself.

Now we show that $F$ is closed in $C_p(\mathbb{S})$ . To this end, we show that

$g \in C_p(\mathbb{S})$

$U$

$g$

$U$

$F$

Actually, this has already been done above with points $g$ that are in $F$ . One thing to point out is that the range of $f_a$ is $\left\{0,1 \right\}$ . As we consider $g \in C_p(\mathbb{S})$ , we only need to consider $g$ that maps into $\left\{0,1 \right\}$ . Let $g \in C_p(\mathbb{S})$ . The argument is given in two cases regarding the function $g$ .

Case 1. There exists some $a \in (0,1)$ such that $g(a) \ne g(-a)$ .

We assume that $g(a)=0$ and $g(-a)=1$ . Then for all $0<b<a$ , $f_b(a)=1$ and for all $a<c<1$ , $f_c(-a)=0$ . Let $U=[a,(-0.1,0.1)] \cap [-a,(0.9,1.1)]$ . Then $g \in U$ and $U$ contains no $f_b$ for any $0<b<a$ and $f_c$ for any $a<c<1$ . To help see this argument, use Figure 6 as a guide. The case that $g(a)=1$ and $g(-a)=0$ has a similar argument.

Case 2. For every $a \in (0,1)$ , we have $g(a) = g(-a)$ .

Claim. The function $g$ is constant on the interval $(-1,1)$ . Suppose not. Let $0<b<a<1$ such that $g(a) \ne g(b)$ . Suppose that $0=g(b) < g(a)=1$ . Consider $W=\left\{w<a: g(w)=0 \right\}$ . Clearly the number $a$ is an upper bound of $W$ . Let $u \le a$ be a least upper bound of $W$ . The function $g$ has value 1 on the interval $(u,a)$ . Otherwise, $u$ would not be the least upper bound of the set $W$ . There is a sequence of points $\left\{x_n \right\}$ in the interval $(b,u)$ such that $x_n \rightarrow u$ from the left such that $g(x_n)=0$ for all $n$ . Otherwise, $u$ would not be the least upper bound of the set $W$ .

It follows that $g(u)=1$ . Otherwise, the function $g$ is not continuous at $u$ . Now consider the 6 points $-a<-u<-b<b<u<a$ . By the assumption in Case 2, $g(u)=g(-u)=1$ and $g(b)=g(-b)=0$ . Since $g(x_n)=0$ for all $n$ , $g(-x_n)=0$ for all $n$ . Note that $-x_n \rightarrow -u$ from the right. Since $g$ is right continuous, $g(-u)=0$ , contradicting $g(-u)=1$ . Thus we cannot have $0=g(b) < g(a)=1$ .

Now suppose we have $1=g(b) > g(a)=0$ where $0<b<a<1$ . Consider $W=\left\{w<a: g(w)=1 \right\}$ . Clearly $W$ has an upper bound, namely the number $a$ . Let $u \le a$ be a least upper bound of $W$ . The function $g$ has value 0 on the interval $(u,a)$ . Otherwise, $u$ would not be the least upper bound of the set $W$ . There is a sequence of points $\left\{x_n \right\}$ in the interval $(b,u)$ such that $x_n \rightarrow u$ from the left such that $g(x_n)=1$ for all $n$ . Otherwise, $u$ would not be the least upper bound of the set $W$ .

It follows that $g(u)=0$ . Otherwise, the function $g$ is not continuous at $u$ . Now consider the 6 points $-a<-u<-b<b<u<a$ . By the assumption in Case 2, $g(u)=g(-u)=0$ and $g(b)=g(-b)=1$ . Since $g(x_n)=1$ for all $n$ , $g(-x_n)=1$ for all $n$ . Note that $-x_n \rightarrow -u$ from the right. Since $g$ is right continuous, $g(-u)=1$ , contradicting $g(-u)=0$ . Thus we cannot have $1=g(b) > g(a)=0$ .

The claim that the function $g$ is constant on the interval $(-1,1)$ is established. To wrap up, first assume that the function $g$ is 1 on the interval $(-1,1)$ . Let $U=[0,(0.9,1.1)]$ . It is clear that $g \in U$ . It is also clear from Figure 5 that $U$ contains no $f_a$ . Now assume that the function $g$ is 0 on the interval $(-1,1)$ . Since $g$ is Sorgenfrey continuous, it follows that $g(-1)=0$ . Let $U=[-1,(-0.1,0.1)]$ . It is clear that $g \in U$ . It is also clear from Figure 5 that $U$ contains no $f_a$ .

We have established that the set $F=\left\{f_a: 0<a<1 \right\}$ is a closed and discrete subspace of $C_p(\mathbb{S})$ .

What does it Mean?

The above argument shows that the set $F$ is a closed an discrete subspace of the function space $C_p(\mathbb{S})$ . We have the following three facts.

Three Results

$C_p(\mathbb{S})$ is separable.
$C_p(\mathbb{S})$ is not hereditarily separable.
$C_p(\mathbb{S})$ is not a normal space.

To show that $C_p(\mathbb{S})$ is separable, let’s look at one basic helpful fact on $C_p(X)$ . If $X$ is a separable metric space, e.g. $X=\mathbb{R}$ , then $C_p(X)$ has quite a few nice properties (discussed here). One is that $C_p(X)$ is hereditarily separable. Thus $C_p(\mathbb{R})$ , the space of real-valued continuous functions defined on the number line with the pointwise convergence topology, is hereditarily separable and thus separable. Recall that continuous functions in $C_p(\mathbb{R})$ are also Soregenfrey line continuous. Thus $C_p(\mathbb{R})$ is a subspace of $C_p(\mathbb{S})$ . The space $C_p(\mathbb{R})$ is also a dense subspace of $C_p(\mathbb{S})$ . Thus the space $C_p(\mathbb{S})$ contains a dense separable subspace. It means that $C_p(\mathbb{S})$ is separable.

Secondly, $C_p(\mathbb{S})$ is not hereditarily separable since the subspace $F=\left\{f_a: 0<a<1 \right\}$ is a closed and discrete subspace.

Thirdly, $C_p(\mathbb{S})$ is not a normal space. According to Jones’ lemma, any separable space with a closed and discrete subspace of cardinality of continuum is not a normal space (see Corollary 1 here). The subspace $F=\left\{f_a: 0<a<1 \right\}$ is a closed and discrete subspace of the separable space $C_p(\mathbb{S})$ . Thus $C_p(\mathbb{S})$ is not normal.

Remarks

The topology of the Sorgenfrey line is vastly different from the usual topology on the real line even though the the Sorgenfrey topology is obtained by a seemingly small tweak from the usual topology. The real line is a metric space while the Sorgenfrey line is not metrizable. The real number line is connected while the Sorgenfrey line is not. The countable power of the real number line is a metric space and thus a normal space. On the other hand, the Sorgenfrey line is a classic example of a normal space whose square is not normal. See here for a basic discussion of the Sorgenfrey line.

The pictures of Sorgenfrey continuous functions demonstrated here show that the real number line and the Sorgenfrey line are also very different from a function space perspective. The function space $C_p(\mathbb{R})$ has a whole host of nice properties: normal, Lindelof (hence paracompact and collectionwise normal), hereditarily Lindelof (hence hereditarily normal), hereditarily separable, and perfectly normal (discussed here).

Though separable, the function space $C_p(\mathbb{S})$ contains a closed and discrete subspace of cardinality continuum, making it not hereditarily separable and not normal.

For more information about $C_p(X)$ in general and $C_p(\mathbb{S})$ in particular, see [1] and [2]. A different proof that $C_p(\mathbb{S})$ contains a closed and discrete subspace of cardinality continuum can be found in Problem 165 in [2].

The next post is a continuation on the theme of drawing Sorgenfrey continuous functions.

Reference

Arkhangelskii, A. V., Topological Function Spaces, Mathematics and Its Applications Series, Kluwer Academic Publishers, Dordrecht, 1992.
Tkachuk V. V., A $C_p$ -Theory Problem Book, Topological and Function Spaces, Springer, New York, 2011.

$\text{ }$

$\copyright$ 2017 – Dan Ma

Normality in Cp(X)

Posted on August 15, 2017 by Dan Ma

Any collectionwise normal space is a normal space. Any perfectly normal space is a hereditarily normal space. In general these two implications are not reversible. In function spaces $C_p(X)$ , the two implications are reversible. There is a normal space that is not countably paracompact (such a space is called a Dowker space). If a function space $C_p(X)$ is normal, it is countably paracompact. Thus normality in $C_p(X)$ is a strong property. This post draws on Dowker’s theorem and other results, some of them are previously discussed in this blog, to discuss this remarkable aspect of the function spaces $C_p(X)$ .

Since we are discussing function spaces, the domain space $X$ has to have sufficient quantity of real-valued continuous functions, e.g. there should be enough continuous functions to separate the points from closed sets. The ideal setting is the class of completely regular spaces (also called Tychonoff spaces). See here for a discussion on completely regular spaces in relation to function spaces.

Let $X$ be a completely regular space. Let $C(X)$ be the set of all continuous functions from $X$ into the real line $\mathbb{R}$ . When $C(X)$ is endowed with the pointwise convergence topology, the space is denoted by $C_p(X)$ (see here for further comments on the definition of the pointwise convergence topology).

When Function Spaces are Normal

Let $X$ be a completely regular space. We discuss these four facts of $C_p(X)$ :

If the function space $C_p(X)$ is normal, then $C_p(X)$ is countably paracompact.
If the function space $C_p(X)$ is hereditarily normal, then $C_p(X)$ is perfectly normal.
If the function space $C_p(X)$ is normal, then $C_p(X)$ is collectionwise normal.
Let $X$ be a normal space. If $C_p(X)$ is normal, then $X$ has countable extent, i.e. every closed and discrete subset of $X$ is countable, implying that $X$ is collectionwise normal.

Fact #1 and Fact #2 rely on a representation of $C_p(X)$ as a product space with one of the factors being the real line. For $x \in X$ , let $Y_x=\left\{f \in C_p(X): f(x)=0 \right\}$ . Then $C_p(X) \cong Y_x \times \mathbb{R}$ . This representation is discussed here.

Another useful tool is Dowker’s theorem, which essentially states that for any normal space $W$ , the space $W$ is countably paracompact if and only if $W \times C$ is normal for all compact metric space $C$ if and only if $W \times [0,1]$ is normal. For the full statement of the theorem, see Theorem 1 in this previous post, which has links to the proofs and other discussion.

To show Fact #1, suppose that $C_p(X)$ is normal. Immediately we make use of the representation $C_p(X) \cong Y_x \times \mathbb{R}$ where $x \in X$ . Since $Y_x \times \mathbb{R}$ is normal, $Y_x \times [0,1]$ is also normal. By Dowker’s theorem, $Y_x$ is countably paracompact. Note that $Y_x$ is a closed subspace of the normal $C_p(X)$ . Thus $Y_x$ is also normal.

One more helpful tool is Theorem 5 in in this previous post, which is like an extension of Dowker’s theorem, which states that a normal space $W$ is countably paracompact if and only if $W \times T$ is normal for any $\sigma$ -compact metric space $T$ . This means that $Y_x \times \mathbb{R} \times \mathbb{R}$ is normal.

We want to show $C_p(X) \cong Y_x \times \mathbb{R}$ is countably paracompact. Since $Y_x \times \mathbb{R} \times \mathbb{R}$ is normal (based on the argument in the preceding paragraph), $(Y_x \times \mathbb{R}) \times [0,1]$ is normal. Thus according to Dowker’s theorem, $C_p(X) \cong Y_x \times \mathbb{R}$ is countably paracompact.

For Fact #2, a helpful tool is Katetov’s theorem (stated and proved here), which states that for any hereditarily normal $X \times Y$ , one of the factors is perfectly normal or every countable subset of the other factor is closed (in that factor).

To show Fact #2, suppose that $C_p(X)$ is hereditarily normal. With $C_p(X) \cong Y_x \times \mathbb{R}$ and according to Katetov’s theorem, $Y_x$ must be perfectly normal. The product of a perfectly normal space and any metric space is perfectly normal (a proof is found here). Thus $C_p(X) \cong Y_x \times \mathbb{R}$ is perfectly normal.

The proof of Fact #3 is found in Problems 294 and 295 of [2]. The key to the proof is a theorem by Reznichenko, which states that any dense convex normal subspace of $[0,1]^X$ has countable extent, hence is collectionwise normal (problem 294). See here for a proof that any normal space with countable extent is collectionwise normal (see Theorem 2). The function space $C_p(X)$ is a dense convex subspace of $[0,1]^X$ (problem 295). Thus if $C_p(X)$ is normal, then it has countable extent and hence collectionwise normal.

Fact #4 says that normality of the function space imposes countable extent on the domain. This result is discussed in this previous post (see Corollary 3 and Corollary 5).

Remarks

The facts discussed here give a flavor of what function spaces are like when they are normal spaces. For further and deeper results, see [1] and [2].

Fact #1 is essentially driven by Dowker’s theorem. It follows from the theorem that whenever the product space $X \times Y$ is normal, one of the factor must be countably paracompact if the other factor has a non-trivial convergent sequence (see Theorem 2 in this previous post). As a result, there is no Dowker space that is a $C_p(X)$ . No pathology can be found in $C_p(X)$ with respect to finding a Dowker space. In fact, not only $C_p(X) \times C$ is normal for any compact metric space $C$ , it is also true that $C_p(X) \times T$ is normal for any $\sigma$ -compact metric space $T$ when $C_p(X)$ is normal.

The driving force behind Fact #2 is Katetov’s theorem, which basically says that the hereditarily normality of $X \times Y$ is a strong statement. Coupled with the fact that $C_p(X)$ is of the form $Y_x \times \mathbb{R}$ , Katetov’s theorem implies that $Y_x \times \mathbb{R}$ is perfectly normal. The argument also uses the basic fact that perfectly normality is preserved when taking product with metric spaces.

There are examples of normal but not collectionwise normal spaces (e.g. Bing’s Example G). Resolution of the question of whether normal but not collectionwise normal Moore space exists took extensive research that spanned decades in the 20th century (the normal Moore space conjecture). The function $C_p(X)$ is outside of the scope of the normal Moore space conjecture. The function space $C_p(X)$ is usually not a Moore space. It can be a Moore space only if the domain $X$ is countable but then $C_p(X)$ would be a metric space. However, it is still a powerful fact that if $C_p(X)$ is normal, then it is collectionwise normal.

On the other hand, a more interesting point is on the normality of $X$ . Suppose that $X$ is a normal Moore space. If $C_p(X)$ happens to be normal, then Fact #4 says that $X$ would have to be collectionwise normal, which means $X$ is metrizable. If the goal is to find a normal Moore space $X$ that is not collectionwise normal, the normality of $C_p(X)$ would kill the possibility of $X$ being the example.

Reference

Arkhangelskii, A. V., Topological Function Spaces, Mathematics and Its Applications Series, Kluwer Academic Publishers, Dordrecht, 1992.
Tkachuk V. V., A $C_p$ -Theory Problem Book, Topological and Function Spaces, Springer, New York, 2011.

$\text{ }$

$\copyright$ 2017 – Dan Ma

Looking for spaces in which every compact subspace is metrizable

Posted on June 11, 2017 by Dan Ma

Once it is known that a topological space is not metrizable, it is natural to ask, from a metrizability standpoint, which subspaces are metrizable, e.g. whether every compact subspace is metrizable. This post discusses several classes of spaces in which every compact subspace is metrizable. Though the goal here is not to find a complete characterization of such spaces, this post discusses several classes of spaces and various examples that have this property. The effort brings together many interesting basic and well known facts. Thus the notion “every compact subspace is metrizable” is an excellent learning opportunity.

Several Classes of Spaces

The notion “every compact subspace is metrizable” is a very broad class of spaces. It includes well known spaces such as Sorgenfrey line, Michael line and the first uncountable ordinal $\omega_1$ (with the order topology) as well as Moore spaces. Certain function spaces are in the class “every compact subspace is metrizable”. The following diagram is a good organizing framework.

$\displaystyle \begin{aligned} &1. \ \text{Metrizable} \\&\ \ \ \ \ \ \ \ \ \Downarrow \\&2. \ \text{Submetrizable} \Longleftarrow 5. \ \exists \ \text{countable network} \\&\ \ \ \ \ \ \ \ \ \Downarrow \\&3. \ \exists \ G_\delta \text{ diagonal} \\&\ \ \ \ \ \ \ \ \ \Downarrow \\&4. \ \text{Every compact subspace is metrizable} \end{aligned}$

Let $(X, \tau)$ be a space. It is submetrizable if there is a topology $\tau_1$ on the set $X$ such that $\tau_1 \subset \tau$ and $(X, \tau_1)$ is a metrizable space. The topology $\tau_1$ is said to be weaker (coarser) than $\tau$ . Thus a space $X$ is submetrizable if it has a weaker metrizable topology.

Let $\mathcal{N}$ be a set of subsets of the space $X$ . $\mathcal{N}$ is said to be a network for $X$ if for every open subset $O$ of $X$ and for each $x \in O$ , there exists $N \in \mathcal{N}$ such that $x \in N \subset O$ . Having a network that is countable in size is a strong property (see here for a discussion on spaces with a countable network).

The diagonal of the space $X$ is the subset $\Delta=\left\{(x,x): x \in X \right\}$ of the square $X \times X$ . The space $X$ has a $G_\delta$ -diagonal if $\Delta$ is a $G_\delta$ -subset of $X \times X$ , i.e. $\Delta$ is the intersection of countably many open subsets of $X \times X$ .

The implication $1 \Longrightarrow 2$ is clear. For $5 \Longrightarrow 2$ , see Lemma 1 in this previous post on countable network. The implication $2 \Longrightarrow 3$ is left as an exercise. To see $3 \Longrightarrow 4$ , let $K$ be a compact subset of $X$ . The property of having a $G_\delta$ -diagonal is hereditary. Thus $K$ has a $G_\delta$ -diagonal. According to a well known result, any compact space with a $G_\delta$ -diagonal is metrizable (see here).

None of the implications in the diagram is reversible. The first uncountable ordinal $\omega_1$ is an example for $4 \not \Longrightarrow 3$ . This follows from the well known result that any countably compact space with a $G_\delta$ -diagonal is metrizable (see here). The Mrowka space is an example for $3 \not \Longrightarrow 2$ (see here). The Sorgenfrey line is an example for both $2 \not \Longrightarrow 5$ and $2 \not \Longrightarrow 1$ .

To see where the examples mentioned earlier are placed, note that Sorgenfrey line and Michael line are submetrizable, both are submetrizable by the usual Euclidean topology on the real line. Each compact subspace of the space $\omega_1$ is countable and is thus contained in some initial segment $[0,\alpha]$ which is metrizable. Any Moore space has a $G_\delta$ -diagonal. Thus compact subspaces of a Moore space are metrizable.

Function Spaces

We now look at some function spaces that are in the class “every compact subspace is metrizable.” For any Tychonoff space (completely regular space) $X$ , $C_p(X)$ is the space of all continuous functions from $X$ into $\mathbb{R}$ with the pointwise convergence topology (see here for basic information on pointwise convergence topology).

Theorem 1
Suppose that $X$ is a separable space. Then every compact subspace of $C_p(X)$ is metrizable.

Proof
The proof here actually shows more than is stated in the theorem. We show that $C_p(X)$ is submetrizable by a separable metric topology. Let $Y$ be a countable dense subspace of $X$ . Then $C_p(Y)$ is metrizable and separable since it is a subspace of the separable metric space $\mathbb{R}^{\omega}$ . Thus $C_p(Y)$ has a countable base. Let $\mathcal{E}$ be a countable base for $C_p(Y)$ .

Let $\pi:C_p(X) \longrightarrow C_p(Y)$ be the restriction map, i.e. for each $f \in C_p(X)$ , $\pi(f)=f \upharpoonright Y$ . Since $\pi$ is a projection map, it is continuous and one-to-one and it maps $C_p(X)$ into $C_p(Y)$ . Thus $\pi$ is a continuous bijection from $C_p(X)$ into $C_p(Y)$ . Let $\mathcal{B}=\left\{\pi^{-1}(E): E \in \mathcal{E} \right\}$ .

We claim that $\mathcal{B}$ is a base for a topology on $C_p(X)$ . Once this is established, the proof of the theorem is completed. Note that $\mathcal{B}$ is countable and elements of $\mathcal{B}$ are open subsets of $C_p(X)$ . Thus the topology generated by $\mathcal{B}$ is coarser than the original topology of $C_p(X)$ .

For $\mathcal{B}$ to be a base, two conditions must be satisfied – $\mathcal{B}$ is a cover of $C_p(X)$ and for $B_1,B_2 \in \mathcal{B}$ , and for $f \in B_1 \cap B_2$ , there exists $B_3 \in \mathcal{B}$ such that $f \in B_3 \subset B_1 \cap B_2$ . Since $\mathcal{E}$ is a base for $C_p(Y)$ and since elements of $\mathcal{B}$ are preimages of elements of $\mathcal{E}$ under the map $\pi$ , it is straightforward to verify these two points. $\square$

Theorem 1 is actually a special case of a duality result in $C_p$ function space theory. More about this point later. First, consider a corollary of Theorem 1.

Corollary 2
Let $X=\prod_{\alpha<c} X_\alpha$ where $c$ is the cardinality continuum and each $X_\alpha$ is a separable space. Then every compact subspace of $C_p(X)$ is metrizable.

The key fact for Corollary 2 is that the product of continuum many separable spaces is separable (this fact is discussed here). Theorem 1 is actually a special case of a deep result.

Theorem 3
Suppose that $X=\prod_{\alpha<\kappa} X_\alpha$ is a product of separable spaces where $\kappa$ is any infinite cardinal. Then every compact subspace of $C_p(X)$ is metrizable.

Theorem 3 is a much more general result. The product of any arbitrary number of separable spaces is not separable if the number of factors is greater than continuum. So the proof for Theorem 1 will not work in the general case. This result is Problem 307 in [2].

A Duality Result

Theorem 1 is stated in a way that gives the right information for the purpose at hand. A more correct statement of Theorem 1 is: $X$ is separable if and only if $C_p(X)$ is submetrizable by a separable metric topology. Of course, the result in the literature is based on density and weak weight.

The cardinal function of density is the least cardinality of a dense subspace. For any space $Y$ , the weight of $Y$ , denoted by $w(Y)$ , is the least cardinaility of a base of $Y$ . The weak weight of a space $X$ is the least $w(Y)$ over all space $Y$ for which there is a continuous bijection from $X$ onto $Y$ . Thus if the weak weight of $X$ is $\omega$ , then there is a continuous bijection from $X$ onto some separable metric space, hence $X$ has a weaker separable metric topology.

There is a duality result between density and weak weight for $X$ and $C_p(X)$ . The duality result:

The density of $X$ coincides with the weak weight of $C_p(X)$ and the weak weight of $X$ coincides with the density of $C_p(X)$ . These are elementary results in $C_p$ -theory. See Theorem I.1.4 and Theorem I.1.5 in [1].

$\text{ }$

Reference

Arkhangelskii, A. V., Topological Function Spaces, Mathematics and Its Applications Series, Kluwer Academic Publishers, Dordrecht, 1992.
Tkachuk V. V., A $C_p$ -Theory Problem Book, Topological and Function Spaces, Springer, New York, 2011.

$\text{ }$

$\copyright$ 2017 – Dan Ma

Comparing two function spaces

Posted on August 5, 2014 by Dan Ma

Let $\omega_1$ be the first uncountable ordinal, and let $\omega_1+1$ be the successor ordinal to $\omega_1$ . Furthermore consider these ordinals as topological spaces endowed with the order topology. It is a well known fact that any continuous real-valued function $f$ defined on either $\omega_1$ or $\omega_1+1$ is eventually constant, i.e., there exists some $\alpha<\omega_1$ such that the function $f$ is constant on the ordinals beyond $\alpha$ . Now consider the function spaces $C_p(\omega_1)$ and $C_p(\omega_1+1)$ . Thus individually, elements of these two function spaces appear identical. Any $f \in C_p(\omega_1)$ matches a function $f^* \in C_p(\omega_1+1)$ where $f^*$ is the result of adding the point $(\omega_1,a)$ to $f$ where $a$ is the eventual constant real value of $f$ . This fact may give the impression that the function spaces $C_p(\omega_1)$ and $C_p(\omega_1+1)$ are identical topologically. The goal in this post is to demonstrate that this is not the case. We compare the two function spaces with respect to some convergence properties (countably tightness and Frechet-Urysohn property) as well as normality.

____________________________________________________________________

Tightness

One topological property that is different between $C_p(\omega_1)$ and $C_p(\omega_1+1)$ is that of tightness. The function space $C_p(\omega_1+1)$ is countably tight, while $C_p(\omega_1)$ is not countably tight.

Let $X$ be a space. The tightness of $X$ , denoted by $t(X)$ , is the least infinite cardinal $\kappa$ such that for any $A \subset X$ and for any $x \in X$ with $x \in \overline{A}$ , there exists $B \subset A$ for which $\lvert B \lvert \le \kappa$ and $x \in \overline{B}$ . When $t(X)=\omega$ , we say that $X$ has countable tightness or is countably tight. When $t(X)>\omega$ , we say that $X$ has uncountable tightness or is uncountably tight.

First, we show that the tightness of $C_p(\omega_1)$ is greater than $\omega$ . For each $\alpha<\omega_1$ , define $f_\alpha: \omega_1 \rightarrow \left\{0,1 \right\}$ such that $f_\alpha(\beta)=0$ for all $\beta \le \alpha$ and $f_\alpha(\beta)=1$ for all $\beta>\alpha$ . Let $g \in C_p(\omega_1)$ be the function that is identically zero. Then $g \in \overline{F}$ where $F$ is defined by $F=\left\{f_\alpha: \alpha<\omega_1 \right\}$ . It is clear that for any countable $B \subset F$ , $g \notin \overline{B}$ . Thus $C_p(\omega_1)$ cannot be countably tight.

The space $\omega_1+1$ is a compact space. The fact that $C_p(\omega_1+1)$ is countably tight follows from the following theorem.

Theorem 1
Let $X$ be a completely regular space. Then the function space $C_p(X)$ is countably tight if and only if $X^n$ is Lindelof for each $n=1,2,3,\cdots$ .

Theorem 1 is a special case of Theorem I.4.1 on page 33 of [1] (the countable case). One direction of Theorem 1 is proved in this previous post, the direction that will give us the desired result for $C_p(\omega_1+1)$ .

____________________________________________________________________

The Frechet-Urysohn property

In fact, $C_p(\omega_1+1)$ has a property that is stronger than countable tightness. The function space $C_p(\omega_1+1)$ is a Frechet-Urysohn space (see this previous post). Of course, $C_p(\omega_1)$ not being countably tight means that it is not a Frechet-Urysohn space.

____________________________________________________________________

Normality

The function space $C_p(\omega_1+1)$ is not normal. If $C_p(\omega_1+1)$ is normal, then $C_p(\omega_1+1)$ would have countable extent. However, there exists an uncountable closed and discrete subset of $C_p(\omega_1+1)$ (see this previous post). On the other hand, $C_p(\omega_1)$ is Lindelof. The fact that $C_p(\omega_1)$ is Lindelof is highly non-trivial and follows from [2]. The author in [2] showed that if $X$ is a space consisting of ordinals such that $X$ is first countable and countably compact, then $C_p(X)$ is Lindelof.

____________________________________________________________________

Embedding one function space into the other

The two function space $C_p(\omega_1+1)$ and $C_p(\omega_1)$ are very different topologically. However, one of them can be embedded into the other one. The space $\omega_1+1$ is the continuous image of $\omega_1$ . Let $g: \omega_1 \longrightarrow \omega_1+1$ be a continuous surjection. Define a map $\psi: C_p(\omega_1+1) \longrightarrow C_p(\omega_1)$ by letting $\psi(f)=f \circ g$ . It is shown in this previous post that $\psi$ is a homeomorphism. Thus $C_p(\omega_1+1)$ is homeomorphic to the image $\psi(C_p(\omega_1+1))$ in $C_p(\omega_1)$ . The map $g$ is also defined in this previous post.

The homeomposhism $\psi$ tells us that the function space $C_p(\omega_1)$ , though Lindelof, is not hereditarily normal.

On the other hand, the function space $C_p(\omega_1)$ cannot be embedded in $C_p(\omega_1+1)$ . Note that $C_p(\omega_1+1)$ is countably tight, which is a hereditary property.

____________________________________________________________________

Remark

There is a mapping that is alluded to at the beginning of the post. Each $f \in C_p(\omega_1)$ is associated with $f^* \in C_p(\omega_1+1)$ which is obtained by appending the point $(\omega_1,a)$ to $f$ where $a$ is the eventual constant real value of $f$ . It may be tempting to think of the mapping $f \rightarrow f^*$ as a candidate for a homeomorphism between the two function spaces. The discussion in this post shows that this particular map is not a homeomorphism. In fact, no other one-to-one map from one of these function spaces onto the other function space can be a homeomorphism.

____________________________________________________________________

Reference

Arkhangelskii, A. V., Topological Function Spaces, Mathematics and Its Applications Series, Kluwer Academic Publishers, Dordrecht, 1992.
Buzyakova, R. Z., In search of Lindelof $C_p$ ‘s, Comment. Math. Univ. Carolinae, 45 (1), 145-151, 2004.

____________________________________________________________________
$\copyright \ 2014 \text{ by Dan Ma}$

Cp(omega 1 + 1) is monolithic and Frechet-Urysohn

Posted on August 4, 2014 by Dan Ma

This is another post that discusses what $C_p(X)$ is like when $X$ is a compact space. In this post, we discuss the example $C_p(\omega_1+1)$ where $\omega_1+1$ is the first compact uncountable ordinal. Note that $\omega_1+1$ is the successor to $\omega_1$ , which is the first (or least) uncountable ordinal. The function space $C_p(\omega_1+1)$ is monolithic and is a Frechet-Urysohn space. Interestingly, the first property is possessed by $C_p(X)$ for all compact spaces $X$ . The second property is possessed by all compact scattered spaces. After we discuss $C_p(\omega_1+1)$ , we discuss briefly the general results for $C_p(X)$ .

____________________________________________________________________

Initial discussion

The function space $C_p(\omega_1+1)$ is a dense subspace of the product space $\mathbb{R}^{\omega_1}$ . In fact, $C_p(\omega_1+1)$ is homeomorphic to a subspace of the following subspace of $\mathbb{R}^{\omega_1}$ :

$\Sigma(\omega_1)=\left\{x \in \mathbb{R}^{\omega_1}: x_\alpha \ne 0 \text{ for at most countably many } \alpha < \omega_1 \right\}$

The subspace $\Sigma(\omega_1)$ is the $\Sigma$ -product of $\omega_1$ many copies of the real line $\mathbb{R}$ . The $\Sigma$ -product of separable metric spaces is monolithic (see here). The $\Sigma$ -product of first countable spaces is Frechet-Urysohn (see here). Thus $\Sigma(\omega_1)$ has both of these properties. Since the properties of monolithicity and being Frechet-Urysohn are carried over to subspaces, the function space $C_p(\omega_1+1)$ has both of these properties. The key to the discussion is then to show that $C_p(\omega_1+1)$ is homeopmophic to a subspace of the $\Sigma$ -product $\Sigma(\omega_1)$ .

____________________________________________________________________

Connection to $\Sigma$ -product

We show that the function space $C_p(\omega_1+1)$ is homeomorphic to a subspace of the $\Sigma$ -product of $\omega_1$ many copies of the real lines. Let $Y_0$ be the following subspace of $C_p(\omega_1+1)$ :

$Y_0=\left\{f \in C_p(\omega_1+1): f(\omega_1)=0 \right\}$

Every function in $Y_0$ has non-zero values at only countably points of $\omega_1+1$ . Thus $Y_0$ can be regarded as a subspace of the $\Sigma$ -product $\Sigma(\omega_1)$ .

By Theorem 1 in this previous post, $C_p(\omega_1+1) \cong Y_0 \times \mathbb{R}$ , i.e, the function space $C_p(\omega_1+1)$ is homeomorphic to the product space $Y_0 \times \mathbb{R}$ . On the other hand, the product $Y_0 \times \mathbb{R}$ can also be regarded as a subspace of the $\Sigma$ -product $\Sigma(\omega_1)$ . Basically adding one additional factor of the real line to $Y_0$ still results in a subspace of the $\Sigma$ -product. Thus we have:

$C_p(\omega_1+1) \cong Y_0 \times \mathbb{R} \subset \Sigma(\omega_1) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)$

Thus $C_p(\omega_1+1)$ possesses all the hereditary properties of $\Sigma(\omega_1)$ . Another observation we can make is that $\Sigma(\omega_1)$ is not hereditarily normal. The function space $C_p(\omega_1+1)$ is not normal (see here). The $\Sigma$ -product $\Sigma(\omega_1)$ is normal (see here). Thus $\Sigma(\omega_1)$ is not hereditarily normal.

____________________________________________________________________

A closer look at $C_p(\omega_1+1)$

In fact $C_p(\omega_1+1)$ has a stronger property that being monolithic. It is strongly monolithic. We use homeomorphic relation in (1) above to get some insight. Let $h$ be a homeomorphism from $C_p(\omega_1+1)$ onto $Y_0 \times \mathbb{R}$ . For each $\alpha<\omega_1$ , let $H_\alpha$ be defined as follows:

$H_\alpha=\left\{f \in C_p(\omega_1+1): f(\gamma)=0 \ \forall \ \alpha<\gamma<\omega_1 \right\}$

Clearly $H_\alpha \subset Y_0$ . Furthermore $H_\alpha$ can be considered as a subspace of $\mathbb{R}^\omega$ and is thus metrizable. Let $A$ be a countable subset of $C_p(\omega_1+1)$ . Then $h(A) \subset H_\alpha \times \mathbb{R}$ for some $\alpha<\omega_1$ . The set $H_\alpha \times \mathbb{R}$ is metrizable. The set $H_\alpha \times \mathbb{R}$ is also a closed subset of $Y_0 \times \mathbb{R}$ . Then $\overline{A}$ is contained in $H_\alpha \times \mathbb{R}$ and is therefore metrizable. We have shown that the closure of every countable subspace of $C_p(\omega_1+1)$ is metrizable. In other words, every separable subspace of $C_p(\omega_1+1)$ is metrizable. This property follows from the fact that $C_p(\omega_1+1)$ is strongly monolithic.

____________________________________________________________________

Monolithicity and Frechet-Urysohn property

As indicated at the beginning, the $\Sigma$ -product $\Sigma(\omega_1)$ is monolithic (in fact strongly monolithic; see here) and is a Frechet-Urysohn space (see here). Thus the function space $C_p(\omega_1+1)$ is both strongly monolithic and Frechet-Urysohn.

Let $\tau$ be an infinite cardinal. A space $X$ is $\tau$ -monolithic if for any $A \subset X$ with $\lvert A \lvert \le \tau$ , we have $nw(\overline{A}) \le \tau$ . A space $X$ is monolithic if it is $\tau$ -monolithic for all infinite cardinal $\tau$ . It is straightforward to show that $X$ is monolithic if and only of for every subspace $Y$ of $X$ , the density of $Y$ equals to the network weight of $Y$ , i.e., $d(Y)=nw(Y)$ . A longer discussion of the definition of monolithicity is found here.

A space $X$ is strongly $\tau$ -monolithic if for any $A \subset X$ with $\lvert A \lvert \le \tau$ , we have $w(\overline{A}) \le \tau$ . A space $X$ is strongly monolithic if it is strongly $\tau$ -monolithic for all infinite cardinal $\tau$ . It is straightforward to show that $X$ is strongly monolithic if and only if for every subspace $Y$ of $X$ , the density of $Y$ equals to the weight of $Y$ , i.e., $d(Y)=w(Y)$ .

In any monolithic space, the density and the network weight coincide for any subspace, and in particular, any subspace that is separable has a countable network. As a result, any separable monolithic space has a countable network. Thus any separable space with no countable network is not monolithic, e.g., the Sorgenfrey line. On the other hand, any space that has a countable network is monolithic.

In any strongly monolithic space, the density and the weight coincide for any subspace, and in particular any separable subspace is metrizable. Thus being separable is an indicator of metrizability among the subspaces of a strongly monolithic space. As a result, any separable strongly monolithic space is metrizable. Any separable space that is not metrizable is not strongly monolithic. Thus any non-metrizable space that has a countable network is an example of a monolithic space that is not strongly monolithic, e.g., the function space $C_p([0,1])$ . It is clear that all metrizable spaces are strongly monolithic.

The function space $C_p(\omega_1+1)$ is not separable. Since it is strongly monolithic, every separable subspace of $C_p(\omega_1+1)$ is metrizable. We can see this by knowing that $C_p(\omega_1+1)$ is a subspace of the $\Sigma$ -product $\Sigma(\omega_1)$ , or by using the homeomorphism $h$ as in the previous section.

For any compact space $X$ , $C_p(X)$ is countably tight (see this previous post). In the case of the compact uncountable ordinal $\omega_1+1$ , $C_p(\omega_1+1)$ has the stronger property of being Frechet-Urysohn. A space $Y$ is said to be a Frechet-Urysohn space (also called a Frechet space) if for each $y \in Y$ and for each $M \subset Y$ , if $y \in \overline{M}$ , then there exists a sequence $\left\{y_n \in M: n=1,2,3,\cdots \right\}$ such that the sequence converges to $y$ . As we shall see below, $C_p(X)$ is rarely Frechet-Urysohn.

____________________________________________________________________

General discussion

For any compact space $X$ , $C_p(X)$ is monolithic but does not have to be strongly monolithic. The monolithicity of $C_p(X)$ follows from the following theorem, which is Theorem II.6.8 in [1].

Theorem 1
Then the function space $C_p(X)$ is monolithic if and only if $X$ is a stable space.

See chapter 3 section 6 of [1] for a discussion of stable spaces. We give the definition here. A space $X$ is stable if for any continuous image $Y$ of $X$ , the weak weight of $Y$ , denoted by $ww(Y)$ , coincides with the network weight of $Y$ , denoted by $nw(Y)$ . In [1], $ww(Y)$ is notated by $iw(Y)$ . The cardinal function $ww(Y)$ is the minimum cardinality of all $w(T)$ , the weight of $T$ , for which there exists a continuous bijection from $Y$ onto $T$ .

All compact spaces are stable. Let $X$ be compact. For any continuous image $Y$ of $X$ , $Y$ is also compact and $ww(Y)=w(Y)$ , since any continuous bijection from $Y$ onto any space $T$ is a homeomorphism. Note that $ww(Y) \le nw(Y) \le w(Y)$ always holds. Thus $ww(Y)=w(Y)$ implies that $ww(Y)=nw(Y)$ . Thus we have:

Corollary 2
Let $X$ be a compact space. Then the function space $C_p(X)$ is monolithic.

However, the strong monolithicity of $C_p(\omega_1+1)$ does not hold in general for $C_p(X)$ for compact $X$ . As indicated above, $C_p([0,1])$ is monolithic but not strongly monolithic. The following theorem is Theorem II.7.9 in [1] and characterizes the strong monolithicity of $C_p(X)$ .

Theorem 3
Let $X$ be a space. Then $C_p(X)$ is strongly monolithic if and only if $X$ is simple.

A space $X$ is $\tau$ -simple if whenever $Y$ is a continuous image of $X$ , if the weight of $Y$ $\le \tau$ , then the cardinality of $Y$ $\le \tau$ . A space $X$ is simple if it is $\tau$ -simple for all infinite cardinal numbers $\tau$ . Interestingly, any separable metric space that is uncountable is not $\omega$ -simple. Thus $[0,1]$ is not $\omega$ -simple and $C_p([0,1])$ is not strongly monolithic, according to Theorem 3.

For compact spaces $X$ , $C_p(X)$ is rarely a Frechet-Urysohn space as evidenced by the following theorem, which is Theorem III.1.2 in [1].

Theorem 4
Let $X$ be a compact space. Then the following conditions are equivalent.

$C_p(X)$ is a Frechet-Urysohn space.
$C_p(X)$ is a k-space.
The compact space $X$ is a scattered space.

A space $X$ is a scattered space if for every non-empty subspace $Y$ of $X$ , there exists an isolated point of $Y$ (relative to the topology of $Y$ ). Any space of ordinals is scattered since every non-empty subset has a least element. Thus $\omega_1+1$ is a scattered space. On the other hand, the unit interval $[0,1]$ with the Euclidean topology is not scattered. According to this theorem, $C_p([0,1])$ cannot be a Frechet-Urysohn space.

____________________________________________________________________

Reference

Arkhangelskii, A. V., Topological Function Spaces, Mathematics and Its Applications Series, Kluwer Academic Publishers, Dordrecht, 1992.

____________________________________________________________________
$\copyright \ 2014 \text{ by Dan Ma}$

A useful representation of Cp(X)

Posted on August 4, 2014 by Dan Ma

Let $X$ be a completely regular space. The space $C_p(X)$ is the space of all real-valued continuous functions defined on $X$ endowed with the pointwise convergence topology. In this post, we show that $C_p(X)$ can be represented as the product of a subspace of $C_p(X)$ with the real line $\mathbb{R}$ . We prove the following theorem. See here for an application of this theorem.

Theorem 1
Let $X$ be a completely regular space. Let $x \in X$ . Let $Y$ be defined by:

$Y=\left\{f \in C_p(X): f(x)=0 \right\}$

Then $C_p(X)$ is homeomorphic to $Y \times \mathbb{R}$ .

The above theorem can be found in [1] (see Theorem I.5.4 on p. 37). In [1], the homeomorphism is stated without proof. For the sake of completeness, we provide a detailed proof of Theorem 1.

Proof of Theorem 1
Define $h: C_p(X) \rightarrow Y \times \mathbb{R}$ by $h(f)=(f-f(x),f(x))$ for any $f \in C_p(X)$ . The map $h$ is a homeomorphism.

The map is one-to-one

First, we show that it is a one-to-one map. Let $f,g \in C_p(X)$ where $f \ne g$ . Assume that $f(x) \ne g(x)$ . Then $h(f) \ne h(g)$ . So assume that $f(x)=g(x)$ . Then the functions $f-f(x)$ and $g-g(x)$ are different, which means $h(f) \ne h(g)$ .

The map is onto

Now we show $h$ maps $C_p(X)$ onto $Y \times \mathbb{R}$ . Let $(g,t) \in Y \times \mathbb{R}$ . Let $f=g+t$ . Note that $f(x)=g(x)+t=t$ . Then $f-f(x)=g$ . We have $h(f)=(g,t)$ .

Note. Showing the continuity of $h$ and $h^{-1}$ is a matter of working with the basic open sets in the function space carefully (e.g. making the necessary shifting). Some authors just skip the details and declare them continuous, e.g. [1]. Readers are welcome to work out enough of the details to see the key idea.

The map is continuous

Show that $h$ is continuous. Let $f \in C_p(X)$ . Let $U \times V$ be an open set in $Y \times \mathbb{R}$ such that $h(f) \in U \times V$ and,

$U=\left\{g \in Y: \forall \ i=1,\cdots,n, g(x_i) \in U_i \right\}$

$\forall \ i=1,\cdots,n, \ U_i=(f(x_i)-f(x)-\frac{1}{k},f(x_i)-f(x)+\frac{1}{k})$

$V=(f(x)-\frac{1}{k},f(x)+\frac{1}{k})$

where $x_1,\cdots,x_n$ are arbitrary points in $X$ and $k$ is some large positive integer. Define the following:

$\forall \ i=1,\cdots,n, \ W_i=(f(x_i)-\frac{1}{2k},f(x_i)+\frac{1}{2k})$

$W_{n+1}=(f(x)-\frac{1}{2k},f(x)+\frac{1}{2k})$

$x_{n+1}=x$

Then define the open set $W$ as follows:

$W=\left\{q \in C_p(X): \forall \ i=1,\cdots,n,n+1, q(x_i) \in W_i \right\}$

Clearly $f \in W$ . We need to show $h(W) \subset U \times V$ . Let $q \in W$ . Then $h(q)=(q-q(x),q(x))$ . We need to show that $q-q(x) \in U$ and $q(x) \in V$ . Note that $q(x_{n+1})=q(x) \in W_{n+1}$ . For each $i=1,\cdots,n$ , $q(x_i) \in W_i$ . So we have the following:

$f(x_i)-\frac{1}{2k}<q(x_i)<f(x_i)+\frac{1}{2k}$

$f(x)-\frac{1}{2k}<q(x)<f(x)+\frac{1}{2k}$

Subtracting the above two inequalities, we have the following:

$f(x_i)-f(x)-\frac{1}{k}<q(x_i)-q(x)<f(x_i)-f(x)+\frac{1}{k}$

The above inequality shows that for each $i=1,\cdots,n$ , $q(x_i) -q(x) \in U_i$ . Hence $q-q(x) \in U$ . It is clear that $q(x) \in V$ . This completes the proof that the map $h$ is continuous.

The inverse is continuous

We now show that $h^{-1}$ is continuous. Let $(g,t) \in Y \times \mathbb{R}$ . Note that $h^{-1}(g,t)=g+t$ . Let $M$ be an open set in $C_p(X)$ such that $g+t \in M$ and

$M=\left\{f \in C_p(X): \forall \ i=1,\cdots,n+1, f(x_i) \in M_i \right\}$

$\forall \ i=1,\cdots,n, \ M_i=(g(x_i)+t-\frac{1}{m},g(x_i)+t+\frac{1}{m})$

$x_{n+1}=x$

$M_{n+1}=(t-\frac{1}{m},t+\frac{1}{m})$

where $x_1,\cdots,x_n$ are arbitrary points of $X$ and $m$ is some large positive integer. Now define an open subset $G \times T$ of $Y \times \mathbb{R}$ such that $(g,t) \in G \times T$ and

$G=\left\{q \in Y: \forall \ i=1,\cdots,n+1, q(x_i) \in G_i \right\}$

$\forall \ i=1,\cdots,n, \ G_i=(g(x_i)-\frac{1}{2m},g(x_i)+\frac{1}{2m})$

$T=(t-\frac{1}{2m},t+\frac{1}{2m})$

We need to show that $h^{-1}(G \times T) \subset M$ . Let $(q,a) \in G \times T$ . We then have the following inequalities.

$\forall \ i=1,\cdots,n, \ g(x_i)-\frac{1}{2m}<q(x_i)<g(x_i)+\frac{1}{2m}$

$t-\frac{1}{2m}<a<t+\frac{1}{2m}$

Adding the above two inequalities, we obtain:

$\forall \ i=1,\cdots,n, \ g(x_i)+t-\frac{1}{m}<q(x_i)+a<g(x_i)+t+\frac{1}{m}$

The above implies that $\forall \ i=1,\cdots,n$ , $q(x_i)+a \in M_i$ . It is clear that $q(x_{n+1})+a=q(x)+a=a \in M_{n+1}$ . Thus $q+a \in M$ . This completes the proof that $h^{-1}$ is continuous.

____________________________________________________________________

Reference

Arkhangelskii, A. V., Topological Function Spaces, Mathematics and Its Applications Series, Kluwer Academic Publishers, Dordrecht, 1992.

____________________________________________________________________
$\copyright \ 2014 \text{ by Dan Ma}$

A useful embedding for Cp(X)

Posted on August 4, 2014 by Dan Ma

Let $X$ be a Tychonoff space (also called completely regular space). By $C_p(X)$ we mean the space of all continuous real-valued functions defined on $X$ endowed with the pointwise convergence topology. In this post we discuss a scenario in which a function space can be embedded into another function space. We prove the following theorem. An example follows the proof.

Theorem 1
Suppose that the space $Y$ is a continuous image of the space $X$ . Then $C_p(Y)$ can be embedded into $C_p(X)$ .

Proof of Theorem 1
Let $t:X \rightarrow Y$ be a continuous surjection, i.e., $t$ is a continuous function from $X$ onto $Y$ . Define the map $\psi: C_p(Y) \rightarrow C_p(X)$ by $\psi(f)=f \circ t$ for all $f \in C_p(Y)$ . We show that $\psi$ is a homeomorphism from $C_p(Y)$ into $C_p(X)$ .

First we show $\psi$ is a one-to-one map. Let $f,g \in C_p(Y)$ with $f \ne g$ . There exists some $y \in Y$ such that $f(y) \ne g(y)$ . Choose some $x \in X$ such that $t(x)=y$ . Then $f \circ t \ne g \circ t$ since $(f \circ t)(x)=f(t(x))=f(y)$ and $(g \circ t)(x)=g(t(x))=g(y)$ .

Next we show that $\psi$ is continuous. Let $f \in C_p(Y)$ . Let $U$ be open in $C_p(X)$ with $\psi(f) \in U$ such that

$U=\left\{q \in C_p(X): \forall \ i=1,\cdots,n, \ q(x_i) \in U_i \right\}$

where $x_1,\cdots,x_n$ are arbitrary points of $X$ and each $U_i$ is an open interval of the real line $\mathbb{R}$ . Note that for each $i$ , $f(t(x_i)) \in U_i$ . Now consider the open set $V$ defined by:

$V=\left\{r \in C_p(Y): \forall \ i=1,\cdots,n, \ r(t(x_i)) \in U_i \right\}$

Clearly $f \in V$ . It follows that $\psi(V) \subset U$ since for each $r \in V$ , it is clear that $\psi(r)=r \circ t \in U$ .

Now we show that $\psi^{-1}: \psi(C_p(Y)) \rightarrow C_p(Y)$ is continuous. Let $\psi(f)=f \circ t \in \psi(C_p(Y))$ where $f \in C_p(Y)$ . Let $G$ be open with $\psi^{-1}(f \circ t)=f \in G$ such that

$G=\left\{r \in C_p(Y): \forall \ i=1,\cdots,m, \ r(y_i) \in G_i \right\}$

where $y_1,\cdots,y_m$ are arbitrary points of $Y$ and each $G_i$ is an open interval of $\mathbb{R}$ . Choose $x_1,\cdots,x_m \in X$ such that $t(x_i)=y_i$ for each $i$ . We have $f(t(x_i)) \in G_i$ for each $i$ . Define the open set $H$ by:

$H=\left\{q \in \psi(C_p(Y)) \subset C_p(X): \forall \ i=1,\cdots,m, \ q(x_i) \in G_i \right\}$

Clearly $f \circ t \in H$ . Note that $\psi^{-1}(H) \subset G$ . To see this, let $r \circ t \in H$ where $r \in C_p(Y)$ . Now $r(t(x_i))=r(y_i) \in G_i$ for each $i$ . Thus $\psi^{-1}(r \circ t)=r \in G$ . It follows that $\psi^{-1}$ is continuous. The proof of the theorem is now complete. $\blacksquare$

____________________________________________________________________

Example

The proof of Theorem 1 is not difficult. It is a matter of notating carefully the open sets in both function spaces. However, the embedding makes it easy in some cases to understand certain function spaces and in some cases to relate certain function spaces.

Let $\omega_1$ be the first uncountable ordinal, and let $\omega_1+1$ be the successor ordinal to $\omega_1$ . Furthermore consider these ordinals as topological spaces endowed with the order topology. As an application of Theorem 1, we show that $C_p(\omega_1+1)$ can be embedded as a subspace of $C_p(\omega_1)$ . Define a continuous surjection $g:\omega_1 \rightarrow \omega_1+1$ as follows:

$g(\gamma) = \begin{cases} \omega_1 & \mbox{if } \ \gamma =0 \\ \gamma-1 & \mbox{if } \ 1 \le \gamma < \omega \\ \gamma & \mbox{if } \ \omega \le \gamma < \omega_1 \end{cases}$

The map $g$ is continuous from $\omega_1$ onto $\omega_1+1$ . By Theorem 1, $C_p(\omega_1+1)$ can be embedded as a subspace of $C_p(\omega_1)$ . On the other hand, $C_p(\omega_1)$ cannot be embedded in $C_p(\omega_1+1)$ . The function space $C_p(\omega_1+1)$ is a Frechet-Urysohn space, which is a property that is carried over to any subspace. The function $C_p(\omega_1)$ is not Frechet-Urysohn. Thus $C_p(\omega_1)$ cannot be embedded in $C_p(\omega_1+1)$ . A further comparison of these two function spaces is found in this subsequent post.

____________________________________________________________________
$\copyright \ 2014 \text{ by Dan Ma}$

Cp(X) is countably tight when X is compact

Posted on August 3, 2014 by Dan Ma

Let $X$ be a completely regular space (also called Tychonoff space). If $X$ is a compact space, what can we say about the function space $C_p(X)$ , the space of all continuous real-valued functions with the pointwise convergence topology? When $X$ is an uncountable space, $C_p(X)$ is not first countable at every point. This follows from the fact that $C_p(X)$ is a dense subspace of the product space $\mathbb{R}^X$ and that no dense subspace of $\mathbb{R}^X$ can be first countable when $X$ is uncountable. However, when $X$ is compact, $C_p(X)$ does have a convergence property, namely $C_p(X)$ is countably tight.

____________________________________________________________________

Tightness

Let $X$ be a completely regular space. The tightness of $X$ , denoted by $t(X)$ , is the least infinite cardinal $\kappa$ such that for any $A \subset X$ and for any $x \in X$ with $x \in \overline{A}$ , there exists $B \subset A$ for which $\lvert B \lvert \le \kappa$ and $x \in \overline{B}$ . When $t(X)=\omega$ , we say that $Y$ has countable tightness or is countably tight. When $t(X)>\omega$ , we say that $X$ has uncountable tightness or is uncountably tight. Clearly any first countable space is countably tight. There are other convergence properties in between first countability and countable tightness, e.g., the Frechet-Urysohn property. The notion of countable tightness and tightness in general is discussed in further details here.

The fact that $C_p(X)$ is countably tight for any compact $X$ follows from the following theorem.

Theorem 1
Let $X$ be a completely regular space. Then the function space $C_p(X)$ is countably tight if and only if $X^n$ is Lindelof for each $n=1,2,3,\cdots$ .

Theorem 1 is the countable case of Theorem I.4.1 on page 33 of [1]. We prove one direction of Theorem 1, the direction that will give us the desired result for $C_p(X)$ where $X$ is compact.

Proof of Theorem 1
The direction $\Longleftarrow$
Suppose that $X^n$ is Lindelof for each positive integer. Let $f \in C_p(X)$ and $f \in \overline{H}$ where $H \subset C_p(X)$ . For each positive integer $n$ , we define an open cover $\mathcal{U}_n$ of $X^n$ .

Let $n$ be a positive integer. Let $t=(x_1,\cdots,x_n) \in X^n$ . Since $f \in \overline{H}$ , there is an $h_t \in H$ such that $\lvert h_t(x_j)-f(x_j) \lvert <\frac{1}{n}$ for all $j=1,\cdots,n$ . Because both $h_t$ and $f$ are continuous, for each $j=1,\cdots,n$ , there is an open set $W(x_j) \subset X$ with $x_j \in W(x_j)$ such that $\lvert h_t(y)-f(y) \lvert < \frac{1}{n}$ for all $y \in W(x_j)$ . Let the open set $U_t$ be defined by $U_t=W(x_1) \times W(x_2) \times \cdots \times W(x_n)$ . Let $\mathcal{U}_n=\left\{U_t: t=(x_1,\cdots,x_n) \in X^n \right\}$ .

For each $n$ , choose $\mathcal{V}_n \subset \mathcal{U}_n$ be countable such that $\mathcal{V}_n$ is a cover of $X^n$ . Let $K_n=\left\{h_t: t \in X^n \text{ such that } U_t \in \mathcal{V}_n \right\}$ . Let $K=\bigcup_{n=1}^\infty K_n$ . Note that $K$ is countable and $K \subset H$ .

We now show that $f \in \overline{K}$ . Choose an arbitrary positive integer $n$ . Choose arbitrary points $y_1,y_2,\cdots,y_n \in X$ . Consider the open set $U$ defined by

$U=\left\{g \in C_p(X): \forall \ j=1,\cdots,n, \lvert g(y_j)-f(y_j) \lvert <\frac{1}{n} \right\}$

We wish to show that $U \cap K \ne \varnothing$ . Choose $U_t \in \mathcal{V}_n$ such that $(y_1,\cdots,y_n) \in U_t$ where $t=(x_1,\cdots,x_n) \in X^n$ . Consider the function $h_t$ that goes with $t$ . It is clear from the way $h_t$ is chosen that $\lvert h_t(y_j)-f(x_j) \lvert<\frac{1}{n}$ for all $j=1,\cdots,n$ . Thus $h_t \in K_n \cap U$ , leading to the conclusion that $f \in \overline{K}$ . The proof that $C_p(X)$ is countably tight is completed.

The direction $\Longrightarrow$
See Theorem I.4.1 of [1].

____________________________________________________________________

Remarks

As shown above, countably tightness is one convergence property of $C_p(X)$ that is guaranteed when $X$ is compact. In general, it is difficult for $C_p(X)$ to have stronger convergence properties such as the Frechet-Urysohn property. It is well known $C_p(\omega_1+1)$ is Frechet-Urysohn. According to Theorem II.1.2 in [1], for any compact space $X$ , $C_p(X)$ is a Frechet-Urysohn space if and only if the compact space $X$ is a scattered space.

____________________________________________________________________

Reference

Arkhangelskii, A. V., Topological Function Spaces, Mathematics and Its Applications Series, Kluwer Academic Publishers, Dordrecht, 1992.

____________________________________________________________________
$\copyright \ 2014 - 2015 \text{ by Dan Ma}$

Cp(omega 1 + 1) is not normal

Posted on August 2, 2014 by Dan Ma

In this and subsequent posts, we consider $C_p(X)$ where $X$ is a compact space. Recall that $C_p(X)$ is the space of all continuous real-valued functions defined on $X$ and that it is endowed with the pointwise convergence topology. One of the compact spaces we consider is $\omega_1+1$ , the first compact uncountable ordinal. There are many interesting results about the function space $C_p(\omega_1+1)$ . In this post we show that $C_p(\omega_1+1)$ is not normal. An even more interesting fact about $C_p(\omega_1+1)$ is that $C_p(\omega_1+1)$ does not have any dense normal subspace [1].

Let $\omega_1$ be the first uncountable ordinal, and let $\omega_1+1$ be the successor ordinal to $\omega_1$ . The set $\omega_1$ is the first uncountable ordinal. Furthermore consider these ordinals as topological spaces endowed with the order topology. As mentioned above, the space $\omega_1+1$ is the first compact uncountable ordinal. In proving that $C_p(\omega_1+1)$ is not normal, a theorem that is due to D. P. Baturov is utilized [2]. This theorem is also proved in this previous post.

For the basic working of function spaces with the pointwise convergence topology, see the post called Working with the function space Cp(X).

The fact that $C_p(\omega_1+1)$ is not normal is established by the following two points.

If $C_p(\omega_1+1)$ is normal, then $C_p(\omega_1+1)$ has countable extent, i.e. every closed and discrete subspace of $C_p(\omega_1+1)$ is countable.
There exists an uncountable closed and discrete subspace of $C_p(\omega_1 +1)$ .

We discuss each of the bullet points separately.

The function space $C_p(\omega_1+1)$ is a dense subspace of $\mathbb{R}^{\omega_1}$ , the product of $\omega_1$ many copies of $\mathbb{R}$ . According to a result of D. P. Baturov [2], any dense normal subspace of the product of $\omega_1$ many separable metric spaces has countable extent (also see Theorem 1a in this previous post). Thus $C_p(\omega_1+1)$ cannot be normal if the second bullet point above is established.

Now we show that there exists an uncountable closed and discrete subspace of $C_p(\omega_1 +1)$ . For each $\alpha$ with $0<\alpha<\omega_1$ , define $h_\alpha:\omega_1 + 1 \rightarrow \left\{0,1 \right\}$ by:

$h_\alpha(\gamma) = \begin{cases} 1 & \mbox{if } \gamma \le \alpha \\ 0 & \mbox{if } \alpha<\gamma \le \omega_1 \end{cases}$

Clearly, $h_\alpha \in C_p(\omega_1 +1)$ for each $\alpha$ . Let $H=\left\{h_\alpha: 0<\alpha<\omega_1 \right\}$ . We show that $H$ is a closed and discrete subspace of $C_p(\omega_1 +1)$ . The fact that $H$ is closed in $C_p(\omega_1 +1)$ is establish by the following claim.

Let $h \in C_p(\omega_1 +1) \backslash H$ . We wish to establish the following claim. Once the claim is established, it follows that $H$ is a closed subset of $C_p(\omega_1 +1)$ .

Claim 1
There exists an open subset $U$ of $C_p(\omega_1 +1)$ such that $h \in U$ and $U \cap H=\varnothing$ .

Consider the two mutually exclusive cases. Case 1. There exists some $\alpha<\omega_1$ such that $h(\alpha) \notin \left\{0,1 \right\}$ . Case 2. $h(\omega_1+1) \subset \left\{0,1 \right\}$ .

For Case 1, let $U=\left\{f \in C_p(\omega_1 +1): f(\alpha) \in \mathbb{R} \backslash \left\{0,1 \right\} \right\}$ . Clearly $h \in U$ and $U \cap H=\varnothing$ .

Now assume Case 2. Within this case, there are three sub cases. Case 2.1. $h$ is a constant function with value 0. Case 2.2. $h$ is a constant function with value 1. Case 2.3. $h$ is not a constant function.

Case 2.1. If $h(\alpha)=0$ for all $\alpha \le \omega_1$ , then consider the open set $U$ where $U=\left\{f \in C_p(\omega_1 +1): f(0) \in \mathbb{R} \backslash \left\{1 \right\} \right\}$ . Clearly $h \in U$ and $U \cap H=\varnothing$ .

Case 2.2. Suppose $h$ is a constant function with value 1. Then let $U$ be the open set: $U=\left\{f \in C_p(\omega_1 +1): f(\omega_1) \in \mathbb{R} \backslash \left\{0 \right\} \right\}$ . It is clear that no function in $H$ can be in $U$ .

Case 2.3. Suppose $h$ is not a constant function. This case be broken down into two cases. Case 2.3.1. $h(\omega_1)=1$ . Case 2.3.2. $h(\omega_1)=0$ .

Case 2.3.1. Just like in Case 2.2, let $U=\left\{f \in C_p(\omega_1 +1): f(\omega_1) \in \mathbb{R} \backslash \left\{0 \right\} \right\}$ . Then $h \in U$ and $U \cap H=\varnothing$ .

Case 2.3.2. Assume that $h(\omega_1)=0$ . Since $h$ is not a constant function, it must takes on a value of 1 at some point. Let $\alpha<\omega_1$ be the largest such that $h(\alpha)=1$ . This $\alpha$ exists because $h$ is continuous and $h(\omega_1)=0$ . This case can be further broken into 2 cases. Case 2.3.2.1. There exists $\beta<\alpha$ such that $h(\beta)=0$ . Case 2.3.2.2. $h(\beta)=1$ for all $\beta<\alpha$ .

Case 2.3.2.1. Define $U=\left\{f \in C_p(\omega_1 +1): f(\beta) \in (-0.1,0.1) \text{ and } f(\alpha) \in (0.9,1.1) \right\}$ . Note that $h \in U$ and $U \cap H=\varnothing$ .

Case 2.3.2.2. In this case, $h(\beta)=1$ for all $\beta \le \alpha$ and $h(\gamma)=0$ for all $\alpha<\gamma \le \omega_1$ . This means that $h=h_\alpha$ . This is a contradiction since $h \notin H$ .

In all the cases except the last one, Claim 1 is true. The last case is not possible. Thus Claim 1 is established. The set $H$ is a closed subset of $C_p(\omega_1 +1)$ .

Next we show that $H$ is discrete in $C_p(\omega_1 +1)$ . Fix $h_\alpha$ where $0<\alpha<\omega_1$ . Let $W=\left\{f \in C_p(\omega_1 +1): f(\alpha) \in (0.9,1.1) \text{ and } f(\alpha+1) \in (-0.1,0.1) \right\}$ . It is clear that $h_\alpha \in W$ . Furthermore, $h_\gamma \notin W$ for all $\alpha < \gamma$ and $h_\gamma \notin W$ for all $\gamma <\alpha$ . Thus $W$ is open such that $\left\{h_\alpha \right\}=W \cap H$ . This completes the proof that $H$ is discrete.

We have established that $H$ is an uncountable closed and discrete subspace of $C_p(\omega_1 +1)$ . This implies that $C_p(\omega_1 +1)$ is not normal.

Remarks

The set $H=\left\{h_\alpha: 0<\alpha<\omega_1 \right\}$ as defined above is closed and discrete in $C_p(\omega_1 +1)$ . However, the set $H$ is not discrete in a larger subspace of the product space. The set $H$ is also a subset of the following $\Sigma$ -product:

$\Sigma(\omega_1)=\left\{x \in \mathbb{R}^{\omega_1}: x_\alpha \ne 0 \text{ for at most countably many } \alpha < \omega_1 \right\}$

Because $\Sigma(\omega_1)$ is the $\Sigma$ -product of separable metric spaces, it is normal (see here). By Theorem 1a in this previous post, $\Sigma(\omega_1)$ would have countable extent. Thus the set $H$ cannot be closed and discrete in $\Sigma(\omega_1)$ . We can actually see this directly. Let $\alpha<\omega_1$ be a limit ordinal. Define $t:\omega_1 + 1 \rightarrow \left\{0,1 \right\}$ by $t(\beta)=1$ for all $\beta<\alpha$ and $t(\beta)=0$ for all $\beta \ge \alpha$ . Clearly $t \notin C_p(\omega_1 +1)$ and $t \in \Sigma(\omega_1)$ . Furthermore, $t \in \overline{H}$ (the closure is taken in $\Sigma(\omega_1)$ ).

The function space $C_p(\omega_1)$ , in contrast, is a Lindelof space and hence a normal space. If we restrict the above defined functions $h_\alpha$ to just $\omega_1$ , would the resulting functions form a closed and discrete set in $C_p(\omega_1)$ ? For each $\alpha$ with $0<\alpha<\omega_1$ , let $g_\alpha=h_\alpha \upharpoonright \omega_1$ . Let $G=\left\{g_\alpha: 0<\alpha<\omega_1 \right\}$ .

Is $G$ a closed and discrete subset of $C_p(\omega_1)$ ? It turns out that $G$ is a discrete subspace of $C_p(\omega_1)$ (relatively discrete). However it is not closed in $C_p(\omega_1)$ . Let $g:\omega_1 \rightarrow \{0, 1\}$ that takes on the constant value of 1. It follows that $g \in \overline{G}$ (the closure is in $C_p(\omega_1)$ ).

It seems that the argument above for showing $H$ is closed and discrete in $C_p(\omega_1+1)$ can be repeated for $G$ . Note that the argument for $H$ relies on the fact that the functions $h_\alpha$ takes on a value at the point $\omega_1$ . So the same argument cannot show that $G$ is a closed and discrete set. Thus $G$ is not discrete in $C_p(\omega_1)$ . Because $C_p(\omega_1)$ is Lindelof (hence normal), it has countable extent. It follows that any uncountable discrete subspace of $C_p(\omega_1)$ cannot be closed in $C_p(\omega_1)$ (the set $G$ is a demonstration). Any uncountable closed subset of $C_p(\omega_1)$ cannot be closed.

Reference

Arhangel’skii, A. V., Normality and Dense Subspaces, Proc. Amer. Math. Soc., 48, no. 2, 283-291, 2001.
Baturov, D. P., Normality in dense subspaces of products, Topology Appl., 36, 111-116, 1990.

Revised 9/17/2018

The canonical evaluation map with a function space perspective

Posted on August 1, 2014 by Dan Ma

The evaluation map is a useful tool for embedding a space into a product space and plays an important role in many theorems and problems in topology. See here for a previous discussion. In this post, we present the evaluation map with the perspective that the map can be used for embedding a space into a function space of continuous functions. This post will be useful background for subsequent posts on $C_p(X)$ . In this post, we take a leisurely approach in setting up the scene. Once the map is defined properly, we show what additional conditions will make the evaluation map a homeomorphism. Then a function space perspective is presented as indicated above. After presenting an application, we conclude with some special cases for evaluation maps.

____________________________________________________________________

The general setting

Let $X$ be a set (later we will add a topology). Let $\mathcal{F}$ be a set of real-valued functions defined on $X$ . Another way to view $\mathcal{F}$ is that it is a subspace of the product space $\mathbb{R}^X$ . For each $x \in X$ , consider the map $\pi_x: \mathbb{R}^X \longrightarrow \mathbb{R}$ defined by $\pi_x(f)=f(x)$ for all $f \in \mathbb{R}^X$ . One way to look at $\pi_x$ is that it is the projection map from the product space $\mathbb{R}^X$ to one of the factors. Thus $\pi_x$ is continuous when $\mathbb{R}^X$ has the product topology. In fact, the product topology is the smallest topology that can be defined on $\mathbb{R}^X$ that would make the $\pi_x$ continuous. When we restrict the map $\pi_x$ to the subspace $\mathcal{F}$ , the map $\pi_x: \mathcal{F} \longrightarrow \mathbb{R}$ is still continuous.

One more comment before defining the evaluation map. The set $\mathcal{F}$ of functions is a subspace of the product space $\mathbb{R}^X$ . Therefore the set $\mathcal{F}$ inherits the subspace topology from the product space. It makes sense to consider the function space $C_p(\mathcal{F})$ , the space of all continuous real-valued functions defined on $\mathcal{F}$ endowed with the pointwise convergence topology. Thus we can write $\pi_x \in C_p(\mathcal{F})$ .

We now define the evaluation map. Define the map $E_\mathcal{F}: X \longrightarrow C_p(\mathcal{F})$ by letting $E_\mathcal{F}(x)=\pi_x$ for each $x \in X$ , or more explicitly, by letting, for each $x \in X$ , $E_\mathcal{F}(x)$ be the map such that $E_\mathcal{F}(x)(f)=f(x)$ for all $f \in \mathcal{F}$ .

The map $E_\mathcal{F}$ is called the evaluation map defined by the family $\mathcal{F}$ . When the set $\mathcal{F}$ is understood, we can omit the subscript and denote the evaluation map by $E$ . We say $E_\mathcal{F}$ is the canonical evaluation map.

____________________________________________________________________

What makes the evaluation map works

The goal of the evaluation map is that it be a homeomorphism. For that to happen, we need to make a few more additional assumptions. In defining the evaluation map above, the functions in the family $\mathcal{F}$ are not required to be continuous. In fact, the set $X$ is just a set in the above section. Now we require that $X$ is a topological space (it must be a completely regular space) and that all functions in $\mathcal{F}$ are continuous. Thus we have $\mathcal{F} \subset C_p(X)$ . With this assumption, the evaluation map is then a continuous function. We have the following theorem.

Theorem 1
Let $X$ be a space. Let $\mathcal{F} \subset C_p(X)$ . Then the evaluation map $E_\mathcal{F}: X \longrightarrow C_p(\mathcal{F})$ is always continuous.

Proof of Theorem 1
Let $x \in X$ . Let $U$ be open in $C_p(\mathcal{F})$ with $E_\mathcal{F}(x)=\pi_x \in U$ such that

$U=\left\{q \in C_p(\mathcal{F}): \forall \ i=1,\cdots,n, \ q(f_i) \in U_i \right\}$

where $f_1,\cdots,f_n$ are arbitrary points of $\mathcal{F}$ and each $U_i$ is an open interval of $\mathbb{R}$ . For each $i=1,\cdots,n$ , $\pi_x(f_i)=f_i(x) \in U_i$ . Let $V=\bigcap_{i=1}^n f_i^{-1}(U_i)$ , which is open in $X$ since each $f_i$ is a continuous function. We show that $E_\mathcal{F}(V) \subset U$ . For each $y \in V$ and for each $i=1,\cdots,n$ , $E_\mathcal{F}(y)(f_i)=\pi_y(f_i)=f_i(y) \in U_i$ . This means that for each $y \in V$ , $E_\mathcal{F}(y)=\pi_y \in U$ . The continuity of the evaluation map is established. $\blacksquare$

In order to make the evaluation map a homeomorphism, we consider two more definitions. A family $\mathcal{F} \subset \mathbb{R}^X$ is said to separate points of $X$ if for any $x,y \in X$ with $x \ne y$ , there exists an $f \in \mathcal{F}$ such that $f(x) \ne f(y)$ . A family $\mathcal{F} \subset \mathbb{R}^X$ is said to separate points from closed subsets of $X$ if for each $x \in X$ and for each closed subset $C$ of $X$ with $x \notin C$ , there exists an $f \in \mathcal{F}$ such that $f(x) \notin \overline{f(C)}$ . We have the following theorem.

Theorem 2
Let $X$ be a space. Let $\mathcal{F} \subset C_p(X)$ . Then the following are true about the evaluation map $E_\mathcal{F}: X \longrightarrow C_p(\mathcal{F})$ .

If $\mathcal{F}$ separates the points of $X$ , then the evaluation map $\mathcal{F}$ is a one-to-one.
If $\mathcal{F}$ separates the points from closed subsets of $X$ , then the evaluation map $\mathcal{F}$ is a homeomorphism.

Proof of Theorem 2
To prove the bullet point 1, suppose that $\mathcal{F}$ separates the points of $X$ . Let $x,y \in X$ with $x \ne y$ . Then there is some $f \in \mathcal{F}$ such that $f(x) \ne f(y)$ . It follows that the functions $E_\mathcal{F}(x)=\pi_x$ and $E_\mathcal{F}(y)=\pi_y$ differ at the point $f \in \mathcal{F}$ . This completes the proof for the bullet 1 of Theorem 2.

To prove the bullet point 2, suppose that the family $\mathcal{F}$ separates the points from closed subsets of $X$ . It suffices to show that the evaluation map $E_\mathcal{F}$ is an open map. Let $U \subset X$ be a non-empty open set. We show that $E_\mathcal{F}(U)$ is open in image $E_\mathcal{F}(X)$ . Let $E_\mathcal{F}(x)=\pi_x \in E_\mathcal{F}(U)$ where $x \in U$ . Since $\mathcal{F}$ separates the points from closed subsets of $X$ , there exists an $f \in \mathcal{F}$ such that $f(x) \notin \overline{f(X \backslash U})$ . Let $V=\mathbb{R}-\overline{f(X \backslash U})$ . Consider the following open set.

$W=\left\{q \in E_\mathcal{F}(X): q(f) \in V \right\}$

Clearly $E_\mathcal{F}(x)=\pi_x \in W$ . We show that $W \subset E_\mathcal{F}(U)$ . Choose $q \in W$ . Then $q=E_\mathcal{F}(y)=\pi_y$ for some $y \in X$ . It is also the case that $q(f)=\pi_y(f)=f(y) \in V$ . Thus $f(y) \notin \overline{f(X \backslash U})$ . This means that $y \in U$ and that $q=E_\mathcal{F}(y)=\pi_y \in E_\mathcal{F}(U)$ . This completes the proof for the bullet 2 of Theorem 2. $\blacksquare$

____________________________________________________________________

Embedding every space into a function space

In defining the evaluation map, we start with a space $X$ . Then take a family of continuous maps $\mathcal{F} \subset C_p(X)$ . As long as the family of functions $\mathcal{F}$ separates points from closed sets, we know for sure that the evaluation map is a homeomorphism from $X$ into a subspace of $C_p(\mathcal{F})$ . We now look at some choices for $\mathcal{F}$ . One is that $\mathcal{F} = C_p(X)$ . Then we have the following corollary.

Corollary 3a
Any space $X$ is homeomorphic to a subspace of the function space $C_p(C_p(X))$ .

Because $X$ is a completely regular space, the family $\mathcal{F} = C_p(X)$ clearly separates points from closed sets. Thus Corollary 3a is valid. In fact, the complete regularity of $X$ only requires that we use $\mathcal{F} = C_p(X,I)$ , the set of all continuous functions from $X$ into $I$ where $I=[0,1]$ . We have the following corollary.

Corollary 3b
Any space $X$ is homeomorphic to a subspace of the function space $C_p(C_p(X,I))$ .

We can also let $\mathcal{F} = C_p^0(X)$ , the set of all bounded real-valued continuous functions defined on $X$ . It is clear that $C_p^0(X)$ separates points from closed sets. So we also have:

Corollary 3c
Any space $X$ is homeomorphic to a subspace of the function space $C_p(C_p^0(X))$ .

____________________________________________________________________

One application

We demonstrate one application of Corollary 3a. When $X$ is a separable metric space, $C_p(X)$ has a countable network (see this previous post). It is natural to ask whether every space with a countable network can be embedded in a $C_p(Y)$ for some separable metric space $Y$ ? The answer is yes. We have the following theorem. One direction of the theorem is Theorem III.1.13 in [1].

Theorem 4
Let $X$ be a space. Then the following conditions are equivalent.

The space $X$ has a countable network.
The space $X$ can be embedded in a $C_p(Y)$ for some separable metric space $Y$ .

Proof of Theorem 4
The direction $2 \longrightarrow 1$ is clear. As shown here, $C_p(Y)$ has a countable network whenever $Y$ has a countable base. Having a countable network carries over to subspaces. The direction $1 \longrightarrow 2$ is the one that uses evaluation map.

$1 \longrightarrow 2$
Suppose that $\mathcal{M}$ is a countable network for $X$ . Then $C_p(X)$ has a countable network, e.g., the set of all $[M,V]$ where $M \in \mathcal{M}$ , $V$ is any open interval with rational endpoints and $[M,V]$ is the set of all $f \in C_p(X)$ such that $f(M) \subset V$ .

Any space with a countable network is the continuous image of a separable metric space. Thus there exists a separable metric space $Y$ such that $C_p(X)$ is the continuous image of $Y$ . Let $g: Y \longrightarrow C_p(X)$ be a continuous surjection. Then $C_p(C_p(X))$ can be embedded into $C_p(Y)$ . The embedding $\rho:C_p(C_p(X)) \longrightarrow C_p(Y)$ is defined by $\rho(f)=f \circ g$ .

By Corollary 3a, $X$ is embedded into $C_p(C_p(X))$ . Then $X$ is embedded into $C_p(Y)$ . $\blacksquare$

____________________________________________________________________

More on the evaluation map

In this section, we consider some special cases. As shown in Theorem 2, what makes the evaluation map a one-to-one map is that the family $\mathcal{F} \subset C_p(X)$ separates points of $X$ (for short, the family is point separating). What makes the evaluation map a homeomorphism is that the family $\mathcal{F}$ separates points from closed subsets of $X$ . In this section, we present one property that implies the property of separating points from closed sets. It is clear that if $\mathcal{F}$ is dense in $C_p(X)$ , then $\mathcal{F}$ separates points of $X$ . In general, the fact that $\mathcal{F}$ is point separating does not mean it separates point from closed sets. We show that whenever $X$ is compact, the fact that $\mathcal{F}$ is dense in $C_p(X)$ does imply that $\mathcal{F}$ separates points from closed sets.

The family $\mathcal{F} \subset C_p(X)$ is said to be a generating set of functions if it determines the topology of $X$ , i.e., the following set is a base for the topology of $X$ .

$\mathcal{B}_{\mathcal{F}}=\left\{f^{-1}(U) \subset X: f \in \mathcal{F} \text{ and } U \text{ is open in } \mathbb{R} \right\}$

Since $X$ is assumed to be a completely regular space, we observe that if $\mathcal{B}_{\mathcal{F}}$ is a base for $X$ , then the family $\mathcal{F}$ separates points from closed subsets of $X$ . The following theorem captures the observations we make.

Theorem 5
Let $X$ be a space. Let $\mathcal{F} \subset C_p(X)$ . Then if $\mathcal{F}$ is a generating set of functions, then $\mathcal{F}$ separates points from closed subsets of $X$ , hence the evaluation map $E_\mathcal{F}: X \longrightarrow C_p(\mathcal{F})$ as defined above is a homeomorphism.

We now show that if $X$ is compact and if $\mathcal{F}$ is dense in $C_p(X)$ , then $\mathcal{F}$ separates points from closed subsets of $X$ , making the evaluation map a homeomorphism.

First one definition. Let $X$ be a space. For any finite $F=\left\{f_1,\cdots,f_n \right\}$ consisting of functions in $C_p(X)$ , define the maximum of $F$ to be the function $f:X \longrightarrow \mathbb{R}$ such that for each $x \in X$ , $f(x)$ is the maximum of the real values in $\left\{f_1(x),\cdots,f_n(x) \right\}$ . In other words, the maximum of $F$ is the pointwise maximum of the functions in $F$ . It is not too difficult to show that the pointwise maximum of finitely many continuous real-valued functions is also continuous. We have the following lemma and corollary.

Lemma 6
Let the space $X$ be compact. Suppose the family $\mathcal{F}$ is dense in $C_p(X)$ such that the pointwise maximum of any finite set of functions in $\mathcal{F}$ is also in $\mathcal{F}$ . Then $\mathcal{F}$ separates points from closed subsets of $X$ .

Proof of Lemma 6
Let $x \in X$ and let $C$ be a closed subset of $X$ such that $x \notin C$ . For each $y \in C$ , consider the open set:

$U_y=\left\{f \in C_p(X): f(x) \in O_1 \text{ and } f(y) \in O_2 \right\}$

where $O_1$ is the open interval $(-0.1,0.1)$ and $O_2$ is the open interval $(2,\infty)$ . For each $y \in C$ , choose $f_y \in \mathcal{F} \cap U_y$ . The set of all $f_y^{-1}(O_2)$ is an open cover of the compact set $C$ . Choose $y_1,y_2,\cdots,y_n \in C$ such that $V_{1},V_{2},\cdots,V_{n}$ cover $C$ where each $V_i=f_{y_i}^{-1}(O_2)$ . Let $g:X \longrightarrow \mathbb{R}$ be the pointwise maximum of $\left\{f_{y_1},\cdots, f_{y_n} \right\}$ . By assumption, $g \in \mathcal{F}$ . It is clear that for all $y \in C$ , $2<g(y)$ . Thus $\overline{g(C)} \subset [2,\infty)$ .

Let $W=\bigcap_{i=1}^n f_{y_i}^{-1}(O_1)$ . It is also clear that $f_{y_i}(x) \in O_1=(-0.1,0.1)$ for all $i$ , implying $g(x) <0.1<1$ . Thus $g(x) \notin \overline{g(C)}$ . Thus completes the proof that $\mathcal{F}$ separates points from closed subsets of $X$ . $\blacksquare$

Corollary 7
Let the space $X$ be compact. If $\mathcal{F}$ is a dense subspace of $C_p(X)$ , then the evaluation map $E_\mathcal{F}: X \longrightarrow C_p(\mathcal{F})$ as defined above is a one-to-one map.

In Corollary 7, even if $\mathcal{F}$ is not closed under taking pointwise maximum of finitely many functions, then throw all pointwise maxima of all finite subsets of $\mathcal{F}$ into $\mathcal{F}$ and then apply Lemma 6. Throwing in all pointwise maxima will not increase the cardinality of $\mathcal{F}$ . For example, suppose that $X$ is compact, $C_p(X)$ is separable and $\mathcal{F}$ is a countable dense subspace of $C_p(X)$ . Even if $\mathcal{F}$ does not contain all the pointwise maxima of finite subspaces, we can then throw in all pointwise maxima and the subspace $\mathcal{F}$ is still countable. Then the compact space $X$ is homeomorphic to a subspace of $C_p(\mathcal{F})$ . Since $C_p(\mathcal{F}) \subset \mathbb{R}^\omega$ , $C_p(\mathcal{F})$ is separable and metrizable. Thus the compact space $X$ is separable and metrizable. The following corollary captures this observation.

Corollary 8
If $X$ is a compact space and the function space $C_p(X)$ is separable, then $X$ is metrizable.

____________________________________________________________________

Reference

Arkhangelskii, A. V., Topological Function Spaces, Mathematics and Its Applications Series, Kluwer Academic Publishers, Dordrecht, 1992.

____________________________________________________________________
$\copyright \ 2014 \text{ by Dan Ma}$

Dan Ma's Topology Blog

Expository Articles In General Topology

Tag Archives: Pointwise convergence topology

Drawing Sorgenfrey continuous functions

Normality in Cp(X)

Looking for spaces in which every compact subspace is metrizable

Comparing two function spaces

Cp(omega 1 + 1) is monolithic and Frechet-Urysohn

A useful representation of Cp(X)

A useful embedding for Cp(X)

Cp(X) is countably tight when X is compact

Cp(omega 1 + 1) is not normal

The canonical evaluation map with a function space perspective