Is every normal dense subspace of a product of separable metric spaces collectionwise normal? This question was posed by Arkhangelskii (see Problem I.5.25 in [2]). One partial positive answer is a theorem attributed to Corson: if  is a normal dense subspace of a product of separable spaces such that
is a normal dense subspace of a product of separable spaces such that 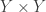 is normal, then
is normal, then  is collectionwise normal. Another partial positive answer: assuming
is collectionwise normal. Another partial positive answer: assuming  , any normal dense subspace of the product space of continuum many separable metric factors is collectionwise normal (see Corollary 4 in this previous post). Another partial positive answer to Arkhangelskii’s question is the theorem due to Reznichenko: If
, any normal dense subspace of the product space of continuum many separable metric factors is collectionwise normal (see Corollary 4 in this previous post). Another partial positive answer to Arkhangelskii’s question is the theorem due to Reznichenko: If 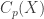 , which is a dense subspace of the product space
, which is a dense subspace of the product space 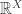 , is normal, then it is collectionwise normal (see Theorem I.5.12 in [2]). In this post, we highlight another partial positive answer to the question posted in [2]. Specifically, we prove the following theorem:
, is normal, then it is collectionwise normal (see Theorem I.5.12 in [2]). In this post, we highlight another partial positive answer to the question posted in [2]. Specifically, we prove the following theorem:
Theorem 1
Let 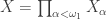 be a product space where each factor
be a product space where each factor  is a separable metric space. Let
is a separable metric space. Let  be a dense subspace of
be a dense subspace of  . Then if
. Then if  is normal, then
is normal, then  is collectionwise normal.
is collectionwise normal.
Since any normal space with countable extent is collectionwise normal (see Theorem 2 in this previous post), it suffices to prove the following theorem:
Theorem 1a
Let 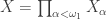 be a product space where each factor
be a product space where each factor  is a separable metric space. Let
is a separable metric space. Let  be a dense subspace of
be a dense subspace of  . Then if
. Then if  is normal, then every closed and discrete subspace of
is normal, then every closed and discrete subspace of  is countable, i.e.,
is countable, i.e.,  has countable extent.
has countable extent.
Arkhangelskii’s question was studied by the author of [3] and [4]. Theorem 1 as presented in this post is essentially the Theorem 1 found in [3]. The proof given in [3] is a beautiful proof. The proof in this post is modeled on the proof in [3] with the exception that all the crucial details are filled in. Theorem 1a (as stated above) is used in [1] to show that the function space  contains no dense normal subspace.
contains no dense normal subspace.
It is natural to wonder if Theorem 1 can be generalized to product space of  many separable metric factors where
many separable metric factors where  is an arbitrary uncountable cardinal. The work of [4] shows that the question at the beginning of this post cannot be answered positively in ZFC. Recall the above mentioned result that assuming
is an arbitrary uncountable cardinal. The work of [4] shows that the question at the beginning of this post cannot be answered positively in ZFC. Recall the above mentioned result that assuming  , any normal dense subspace of the product space of continuum many separable metric factors is collectionwise normal (see Corollary 4 in this previous post). A theorem in [4] implies that assuming
, any normal dense subspace of the product space of continuum many separable metric factors is collectionwise normal (see Corollary 4 in this previous post). A theorem in [4] implies that assuming  , for any separable metric space
, for any separable metric space  with at least 2 points, the product of continuum many copies of
with at least 2 points, the product of continuum many copies of  contains a normal dense subspace
contains a normal dense subspace  that is not collectionwise normal. A side note: for this normal subspace
that is not collectionwise normal. A side note: for this normal subspace  ,
, 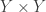 is necessarily not normal (according to Corson’s theorem). Thus [3] and [4] collectively show that Arkhangelskii’s question stated here at the beginning of the post is answered positively (in ZFC) among product spaces of
is necessarily not normal (according to Corson’s theorem). Thus [3] and [4] collectively show that Arkhangelskii’s question stated here at the beginning of the post is answered positively (in ZFC) among product spaces of  many separable metric factors and that outside of the
many separable metric factors and that outside of the  case, it is impossible to answer the question positively in ZFC.
case, it is impossible to answer the question positively in ZFC.
____________________________________________________________________
Proving Theorem 1a
We use the following lemma. For a proof of this lemma, see the proof for Lemma 1 in this previous post.
Lemma 2
Let 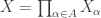 be a product of separable metrizable spaces. Let
be a product of separable metrizable spaces. Let  be a dense subspace of
be a dense subspace of  . Then the following conditions are equivalent.
. Then the following conditions are equivalent.
 is normal.
is normal.- For any pair of disjoint closed subsets
 and
and  of
of  , there exists a countable
, there exists a countable  such that
such that 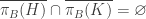 .
.
- For any pair of disjoint closed subsets
 and
and  of
of  , there exists a countable
, there exists a countable  such that
such that  and
and 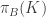 are separated in
are separated in  , meaning that
, meaning that  .
.
For any  , let
, let  be the natural projection from the product space
be the natural projection from the product space 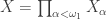 into the subproduct space
into the subproduct space  .
.
Proof of Theorem 1a
Let  be a dense subspace of the product space
be a dense subspace of the product space 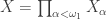 where each factor
where each factor  has a countable base. Suppose that
has a countable base. Suppose that  is an uncountable closed and discrete subset of
is an uncountable closed and discrete subset of  . We then construct a pair of disjoint closed subsets
. We then construct a pair of disjoint closed subsets  and
and  of
of  such that for all countable
such that for all countable  ,
,  and
and 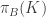 are not separated, specifically
are not separated, specifically 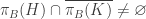 . Here the closure is taken in the space
. Here the closure is taken in the space  . By Lemma 2, the dense subspace
. By Lemma 2, the dense subspace  of
of  is not normal.
is not normal.
For each  , let
, let 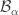 be a countable base for the space
be a countable base for the space  . The standard basic open sets in the product space
. The standard basic open sets in the product space  are of the form
are of the form  such that
such that
- each
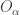 is an open subset of
is an open subset of  ,
,
- if
 , then
, then  ,
,
 for all but finitely many
for all but finitely many  .
.
We use  to denote the finite set of
to denote the finite set of  such that
such that  . Technically we should be working with standard basic open subsets of
. Technically we should be working with standard basic open subsets of  , i.e., sets of the form
, i.e., sets of the form 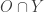 where
where 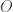 is a standard basic open set as described above. Since
is a standard basic open set as described above. Since  is dense in the product space, every standard open set contains points of
is dense in the product space, every standard open set contains points of  . Thus we can simply work with standard basic open sets in the product space as long as we are working with points of
. Thus we can simply work with standard basic open sets in the product space as long as we are working with points of  in the construction.
in the construction.
Let 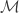 be the collection of all standard basic open sets as described above. Since there are only
be the collection of all standard basic open sets as described above. Since there are only  many factors in the product space,
many factors in the product space, 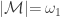 . Recall that
. Recall that  is an uncountable closed and discrete subset of
is an uncountable closed and discrete subset of  . Let
. Let 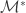 be the following:
be the following:
Claim 1.  .
.
First we show that 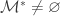 . Let
. Let  be countable. Consider these two cases: Case 1.
be countable. Consider these two cases: Case 1.  is an uncountable subset of
is an uncountable subset of  ; Case 2.
; Case 2.  is countable.
is countable.
Suppose Case 1 is true. Since  is a product of countably many separable metric spaces, it is hereditarily Lindelof. Then there exists a point
is a product of countably many separable metric spaces, it is hereditarily Lindelof. Then there exists a point 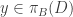 such that every open neighborhood of
such that every open neighborhood of  (open in
(open in  ) contains uncountably many points of
) contains uncountably many points of  . Thus every standard basic open set
. Thus every standard basic open set 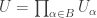 , with
, with 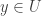 , contains uncountably many points of
, contains uncountably many points of  . Suppose Case 2 is true. There exists one point
. Suppose Case 2 is true. There exists one point 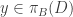 such that
such that  for uncountably many
for uncountably many 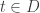 . Then in either case, every standard basic open set
. Then in either case, every standard basic open set  , with
, with  and
and 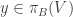 , contains uncountably many points of
, contains uncountably many points of  . Any one such
. Any one such  is a member of
is a member of 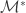 .
.
We can partition the index set  into
into  many disjoint countable sets
many disjoint countable sets  . Then for each such
. Then for each such  , obtain a
, obtain a 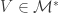 in either Case 1 or Case 2. Since
in either Case 1 or Case 2. Since  , all such open sets
, all such open sets  are distinct. Thus Claim 1 is established.
are distinct. Thus Claim 1 is established.
Claim 2.
There exists an uncountable 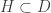 such that for each
such that for each 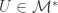 ,
, 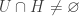 and
and  .
.
Enumerate 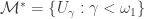 . Choose
. Choose 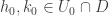 with
with 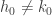 . Suppose that for all
. Suppose that for all 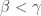 , two points
, two points 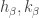 are chosen such that
are chosen such that 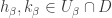 ,
, 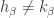 and such that
and such that 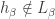 and
and 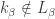 where
where 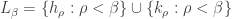 . Then choose
. Then choose 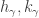 with
with 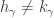 such that
such that 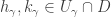 and
and 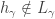 and
and 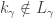 where
where 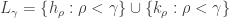 .
.
Let  and let
and let  . Note that
. Note that 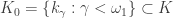 . Based on the inductive process that is used to obtain
. Based on the inductive process that is used to obtain  and
and  , it is clear that
, it is clear that  satisfies Claim 2.
satisfies Claim 2.
Claim 3.
For each countable  , the sets
, the sets  and
and 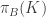 are not separated in the space
are not separated in the space  .
.
Let  be countable. Consider the two cases: Case 1.
be countable. Consider the two cases: Case 1.  is uncountable; Case 2.
is uncountable; Case 2.  is countable. Suppose Case 1 is true. Since
is countable. Suppose Case 1 is true. Since  is a product of countably many separable metric spaces, it is hereditarily Lindelof. Then there exists a point
is a product of countably many separable metric spaces, it is hereditarily Lindelof. Then there exists a point 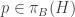 such that every open neighborhood of
such that every open neighborhood of  (open in
(open in  ) contains uncountably many points of
) contains uncountably many points of  . Choose
. Choose  such that
such that  . Then the following statement holds:
. Then the following statement holds:
- For every basic open set
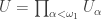 with
with 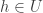 such that
such that  , the open set
, the open set  contains uncountably many points of
contains uncountably many points of  .
.
Suppose Case 2 is true. There exists some 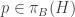 such that
such that  for uncountably many
for uncountably many  . Choose
. Choose  such that
such that  . Then statement 1 also holds.
. Then statement 1 also holds.
In either case, there exists  such that statement 1 holds. The open sets
such that statement 1 holds. The open sets  described in statement 1 are members of
described in statement 1 are members of 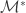 . By Claim 2, the open sets described in statement 1 also contain points of
. By Claim 2, the open sets described in statement 1 also contain points of  . Since the open sets described in statement 1 have supports
. Since the open sets described in statement 1 have supports 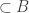 , the following statement holds:
, the following statement holds:
- For every basic open set
 with
with  , the open set
, the open set  contains points of
contains points of 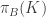 .
.
Statement 2 indicates that 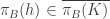 . Thus
. Thus 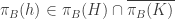 . The closure here can be taken in either
. The closure here can be taken in either  or
or  (to apply Lemma 2, we only need the latter). Thus Claim 3 is established.
(to apply Lemma 2, we only need the latter). Thus Claim 3 is established.
Claim 3 is the negation of condition 3 of Lemma 2. Therefore  is not normal.
is not normal. 
____________________________________________________________________
Remark
The proof of Theorem 1a, though a proof in ZFC only, clearly relies on the fact that the product space is a product of  many factors. For example, in the inductive step in the proof of Claim 2, it is always possible to pick a pair of points not chosen previously. This is because the previously chosen points form a countable set and each open set in
many factors. For example, in the inductive step in the proof of Claim 2, it is always possible to pick a pair of points not chosen previously. This is because the previously chosen points form a countable set and each open set in 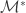 contains
contains  many points of the closed and discrete set
many points of the closed and discrete set  . With the “
. With the “ versus
versus  ” situation, at each step, there are always points not previously chosen. When more than
” situation, at each step, there are always points not previously chosen. When more than  many factors are involved, there may be no such guarantee in the inductive process.
many factors are involved, there may be no such guarantee in the inductive process.
____________________________________________________________________
Reference
- Arkhangelskii, A. V., Normality and dense subspaces, Proc. Amer. Math. Soc., 130 (1), 283-291, 2001.
- Arkhangelskii, A. V., Topological Function Spaces, Mathematics and Its Applications Series, Kluwer Academic Publishers, Dordrecht, 1992.
- Baturov, D. P., Normality in dense subspaces of products, Topology Appl., 36, 111-116, 1990.
- Baturov, D. P., On perfectly normal dense subspaces of products, Topology Appl., 154, 374-383, 2007.
- Engelking, R., General Topology, Revised and Completed edition, Heldermann Verlag, Berlin, 1989.
____________________________________________________________________

is Lindelof if every open cover
has a countable subcollection that also is a cover of
. A topological space
is hereditarily Lindelof if every subspace of
, with respect to the subspace topology, is a Lindelof space. In this post, we prove a theorem that gives two equivalent conditions for the hereditarily Lindelof property. We consider the following theorem.
be a topological space. The following conditions are equivalent.
is a hereditarily Lindelof space.
is Lindelof.
of
, there exists a point
such that every open subset of
containing
contains uncountably many points of
.
is the exercise 3.12.7(d) on page 224 of [1]. The equivalence of the 3 conditions of Theorem 1 is mentioned on page 182 (chapter d-8) of [2].
is immediate. The direction
is straightforward.
. Suppose
is a non-Lindelof subspace of
. Let
be an open cover of
such that no countable subcollection of
can cover
. By a transfinite inductive process, choose a set of points
and a collection of open sets
such that for each
,
and
. The inductive process is possible since no countable subcollection of
can cover
. Now let
. Note that each
can at most contain countably many points of
, namely the points in
.
, let
be an open subset of
such that
. We can now conclude: for every point
of
, there exists an open set
containing
such that
contains only countably many points of
. This is the negation of condition 3.
. We say
is a limit point of the set
if every open set containing
contains a point of
different from
. Being a limit point of
, we only know that each open set containing
contain infinitely many points of
(assuming a
space). Thus the limit points indicated in condition 3 are a special type of limit points. According to the terminology of [1], if
is a limit point of
satisfying condition 3, then
is said to be a condensation point of
. According to Theorem 1, existence of condensation point in every uncountable set is a strong topological property (being equivalent to the hereditarily property). It is easy to see that of condition 3 holds, all but countably many points of any uncountable set
is a condensation point of
.
is hereditarily Lindelof, then every uncountable subspace
of
contains one of its limit points.
is Lindelof, then every uncountable subspace
of
has a limit point.
of
has a limit point” has another name. When a space satisfies this condition, it is said to have countable extent. The ideas in Corollary 2 and Theorem 3 are also discussed in this previous post.
