This is a small attempt toward making sense of the spaces with small diagonal. What makes the property of small diagonal interesting is the longstanding open problem that is discussed below. We use examples to help make sense of the definition of small diagonal. Then we discuss briefly the open problem regarding small diagonal. We discuss the following three examples of compact spaces:
 with the ordered topology
with the ordered topology- The one-point compactification of a discrete space of cardinality

- The double arrow space
By a space we mean a topological space that is Tychonoff, i.e. Hausdorff and completely regular (defined here). Let  be a space. The subset
be a space. The subset 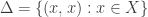 of the square
of the square 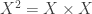 is called the diagonal of the space
is called the diagonal of the space  .
.
We want to focus on two diagonal properties. The space  is said to have a
is said to have a  -diagonal if
-diagonal if  is a
is a  -set in
-set in 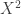 , i.e.
, i.e.  is the intersection of countably many open subsets of
is the intersection of countably many open subsets of 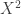 . The space
. The space  is said to have a small diagonal if for each uncountable subset
is said to have a small diagonal if for each uncountable subset  of
of  , there is an open subset
, there is an open subset 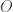 of
of 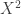 such that
such that  and
and  misses uncountably many points of
misses uncountably many points of  .
.
How do these two diagonal properties relate? Any space that has a  -diagonal also has a small diagonal. This fact can be worked out quite easily based on the definitions. The opposite direction is a totally different matter. In fact, the question of whether having a small diagonal implies having a
-diagonal also has a small diagonal. This fact can be worked out quite easily based on the definitions. The opposite direction is a totally different matter. In fact, the question of whether having a small diagonal implies having a  -diagonal is related to a longstanding open question.
-diagonal is related to a longstanding open question.
Let’s focus on compact spaces. A classic metrization theorem for compact spaces states that any compact space with a  -diagonal is metrizable (see here). A natural question is: if a compact space has a small diagonal, must it be metrizable? Indeed this is a well known open problem, a longstanding problem that has not completely resolved completely. Before discussion the open problem, we look at the three examples indicated above.
-diagonal is metrizable (see here). A natural question is: if a compact space has a small diagonal, must it be metrizable? Indeed this is a well known open problem, a longstanding problem that has not completely resolved completely. Before discussion the open problem, we look at the three examples indicated above.
The three examples are all non-metrizable compact spaces and thus do not have a  -diagonal. We show that they also not have a small diagonal. To appreciate the definition of small diagonal, it is helpful to look spaces that do not have a small diagonal.
-diagonal. We show that they also not have a small diagonal. To appreciate the definition of small diagonal, it is helpful to look spaces that do not have a small diagonal.
Example 1
Consider 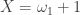 with the order topology. Using interval notion,
with the order topology. Using interval notion, ![X=[0,\omega_1]](https://s0.wp.com/latex.php?latex=X%3D%5B0%2C%5Comega_1%5D&bg=ffffff&fg=333333&s=0&c=20201002) . This is the space of all countable ordinals
. This is the space of all countable ordinals  plus the point
plus the point  at the end. This is a compact space that is not metrizable. For example, any compact metrizable space would be separable. The last point
at the end. This is a compact space that is not metrizable. For example, any compact metrizable space would be separable. The last point  cannot be in the closure of any countable subset. According to the classic theorem mentioned above,
cannot be in the closure of any countable subset. According to the classic theorem mentioned above, ![X=[0,\omega_1]](https://s0.wp.com/latex.php?latex=X%3D%5B0%2C%5Comega_1%5D&bg=ffffff&fg=333333&s=0&c=20201002) cannot have a
cannot have a  -diagonal. We show that it does have a small diagonal too.
-diagonal. We show that it does have a small diagonal too.
Let 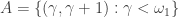 . Note that any open set of the form
. Note that any open set of the form ![(\alpha, \omega_1] \times (\alpha, \omega_1]](https://s0.wp.com/latex.php?latex=%28%5Calpha%2C+%5Comega_1%5D+%5Ctimes+%28%5Calpha%2C+%5Comega_1%5D&bg=ffffff&fg=333333&s=0&c=20201002) contains the point
contains the point  and contains all but countably many points of
and contains all but countably many points of  . As a result, any open set containing the diagonal
. As a result, any open set containing the diagonal  contains all but countably many points of
contains all but countably many points of  . This violates the definition of having a small diagonal. Thus the space
. This violates the definition of having a small diagonal. Thus the space ![X=[0,\omega_1]](https://s0.wp.com/latex.php?latex=X%3D%5B0%2C%5Comega_1%5D&bg=ffffff&fg=333333&s=0&c=20201002) does not have a small diagonal.
does not have a small diagonal.
More on the Definition
Example 1 suggests a different angle in looking at the definition. The set 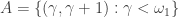 is a
is a  -length sequence convergent to the diagonal, meaning that any open set containing the diagonal contains a tail of the sequence (in this case containing all but countably many elements in the sequence). The convergent sequence view point is the way Husek defined small diagonal [7].
-length sequence convergent to the diagonal, meaning that any open set containing the diagonal contains a tail of the sequence (in this case containing all but countably many elements in the sequence). The convergent sequence view point is the way Husek defined small diagonal [7].
In [7],  is said to have an
is said to have an  -accessible diagonal if there is an
-accessible diagonal if there is an  -length sequence
-length sequence  that converges to the diagonal
that converges to the diagonal  , meaning that any open set containing
, meaning that any open set containing  contains all but countably many terms in the sequence. This is exactly what is occurring in the space
contains all but countably many terms in the sequence. This is exactly what is occurring in the space ![X=[0,\omega_1]](https://s0.wp.com/latex.php?latex=X%3D%5B0%2C%5Comega_1%5D&bg=ffffff&fg=333333&s=0&c=20201002) . The set
. The set 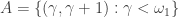 is precisely a convergent sequence converging to the diagonal. The space
is precisely a convergent sequence converging to the diagonal. The space ![X=[0,\omega_1]](https://s0.wp.com/latex.php?latex=X%3D%5B0%2C%5Comega_1%5D&bg=ffffff&fg=333333&s=0&c=20201002) has an
has an  -accessible diagonal.
-accessible diagonal.
Seen in this light, spaces with a small diagonal are the the spaces that do not have an  -accessible diagonal (or spaces that have an
-accessible diagonal (or spaces that have an  -inaccessible diagonal). Though the definition of Husek is more descriptive, the term small diagonal, suggested by E. van Douwen, has become more popular. The small diagonal defined above is more positive sounding. For example, we say the space
-inaccessible diagonal). Though the definition of Husek is more descriptive, the term small diagonal, suggested by E. van Douwen, has become more popular. The small diagonal defined above is more positive sounding. For example, we say the space  has a small diagonal. In Husek [7], the spaces of interest would be the spaces without an
has a small diagonal. In Husek [7], the spaces of interest would be the spaces without an  -accessible diagonal. This definition is a negative one (defined by the lack of certain thing) and takes more syllables to express. Personally speaking, we prefer the term small diagonal though we understand that
-accessible diagonal. This definition is a negative one (defined by the lack of certain thing) and takes more syllables to express. Personally speaking, we prefer the term small diagonal though we understand that  -accessible diagonal is more descriptive.
-accessible diagonal is more descriptive.
A slightly different (but equivalent) way of stating the definition of a space with a small diagonal: a space  has a small diagonal if for any uncountable
has a small diagonal if for any uncountable  , there is an uncountable
, there is an uncountable  such that
such that  . In the literature, the definition of a space with a small diagonal is usually either this one or the one given at the beginning of this post.
. In the literature, the definition of a space with a small diagonal is usually either this one or the one given at the beginning of this post.
Example 2
Now consider the space 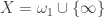 where points in
where points in  are isolated and open neighborhoods of the point
are isolated and open neighborhoods of the point  are of the form
are of the form 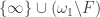 with
with  being any finite subset of
being any finite subset of  . This is usually called the one-point compactification of a discrete space (in this case of size
. This is usually called the one-point compactification of a discrete space (in this case of size  ). This space is compact. It is also non-metrizable since it has an uncountable discrete subset. Thus it cannot have a
). This space is compact. It is also non-metrizable since it has an uncountable discrete subset. Thus it cannot have a  -diagonal. The weight of
-diagonal. The weight of  here is
here is  . Any compact space whose weight is
. Any compact space whose weight is  cannot have a small diagonal. This is Fact 1 below.
cannot have a small diagonal. This is Fact 1 below.
Some Basic Results
Fact 1
Let  any compact space with
any compact space with 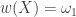 . Then
. Then  does not have a small diagonal.
does not have a small diagonal.
Proof of Fact 1
Let 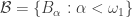 be a base for
be a base for  . Let
. Let 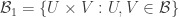 , which is a base for
, which is a base for 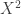 . Define
. Define  . Since
. Since  is compact, the diagonal
is compact, the diagonal  is compact. As a result,
is compact. As a result,  . Furthermore,
. Furthermore, 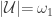 .
.
We claim that  is a base for the diagonal
is a base for the diagonal  . To show this, let
. To show this, let  be an open subset of
be an open subset of 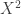 such that
such that 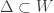 . We can assume that
. We can assume that  is the union of elements of the base
is the union of elements of the base  . Let
. Let 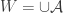 for some
for some 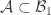 . Since
. Since  is compact,
is compact,  for some finite
for some finite 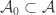 . Note that
. Note that  and that
and that  .
.
Enumerate  as
as  . Since
. Since  is compact and has uncountable weight,
is compact and has uncountable weight,  is not metrizable. Hence the diagonal
is not metrizable. Hence the diagonal  is not a
is not a  -set. As a result, for each
-set. As a result, for each  ,
, 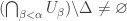 . Furthermore, for any countable
. Furthermore, for any countable 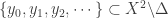 ,
, ![[(\bigcap_{\beta<\alpha} U_\beta) \cap (\bigcap_{n \in \omega} X^2 \backslash \{ y_n \}) ]\backslash \Delta \ne \varnothing](https://s0.wp.com/latex.php?latex=%5B%28%5Cbigcap_%7B%5Cbeta%3C%5Calpha%7D+U_%5Cbeta%29+%5Ccap+%28%5Cbigcap_%7Bn+%5Cin+%5Comega%7D+X%5E2+%5Cbackslash+%5C%7B+y_n+%5C%7D%29+%5D%5Cbackslash+%5CDelta+%5Cne+%5Cvarnothing&bg=ffffff&fg=333333&s=0&c=20201002) .
.
Pick 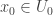 . For any
. For any  with
with  , choose
, choose  .
.
Then the sequence  converges to the diagonal
converges to the diagonal  . To see this, fix
. To see this, fix 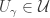 . From the way the sequence is chosen,
. From the way the sequence is chosen,  for all
for all  . This concludes the proof that
. This concludes the proof that  does not have a small diagonal.
does not have a small diagonal. 
Fact 2
Let  any compact space with
any compact space with  . Then if
. Then if  has a small diagonal, then
has a small diagonal, then  and thus
and thus  is metrizable.
is metrizable.
Fact 2 is an easy corollary of Fact 1. Fact 2 says that any compact space with “small” weight (no more than  ) is metrizable if it has a small diagonal. Both Example 1 and Example 2 are compact non-metrizable spaces with small weight. Therefore they do not have small diagonal. The following basic fact is also useful.
) is metrizable if it has a small diagonal. Both Example 1 and Example 2 are compact non-metrizable spaces with small weight. Therefore they do not have small diagonal. The following basic fact is also useful.
Fact 3
Let  any compact space. Then if
any compact space. Then if  has a small diagonal, then
has a small diagonal, then 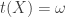 , i.e.
, i.e.  is countably tight.
is countably tight.
Proof of Fact 3
Suppose  is uncountably tight. We show that it does not have a small diagonal. A sequence of points
is uncountably tight. We show that it does not have a small diagonal. A sequence of points  is a free sequence of length
is a free sequence of length  if for each
if for each 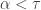 ,
,  . For any compact space with tightness at least
. For any compact space with tightness at least  , there exists a free sequence of length
, there exists a free sequence of length  (see Lemma 2 here). Thus in the space
(see Lemma 2 here). Thus in the space  in question, there exists a free sequence
in question, there exists a free sequence 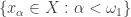 .
.
The main result in [9] says that if a compact space contains a free sequence of length  , then it contains a free sequence of the same length that is convergent. We now assume that the above free sequence
, then it contains a free sequence of the same length that is convergent. We now assume that the above free sequence 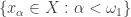 is also convergent, i.e. it converges to some point
is also convergent, i.e. it converges to some point 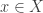 . Thus every open set containing
. Thus every open set containing  contains all but countably many
contains all but countably many 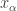 . Consider the sequence
. Consider the sequence 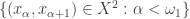 . Observe that every open set in
. Observe that every open set in 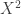 containing the point
containing the point  contains all but countably pairs
contains all but countably pairs  . This implies that every open set containing the diagonal
. This implies that every open set containing the diagonal  contains all but countably many points in the sequence. This shows that the compact
contains all but countably many points in the sequence. This shows that the compact  does not have a small diagonal.
does not have a small diagonal. 
According to Fact 3, the compact ordinal ![\omega_1+1=[0, \omega_1]](https://s0.wp.com/latex.php?latex=%5Comega_1%2B1%3D%5B0%2C+%5Comega_1%5D&bg=ffffff&fg=333333&s=0&c=20201002) does not have a small diagonal since it is uncountably tight at the last point
does not have a small diagonal since it is uncountably tight at the last point  .
.
Example 3
We now consider the double arrow space. Let ![D=[0,1] \times \{0, 1 \}](https://s0.wp.com/latex.php?latex=D%3D%5B0%2C1%5D+%5Ctimes+%5C%7B0%2C+1+%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) . The space
. The space  consists of two copies of the unit interval, an upper one and a lower one. See the first two diagrams in this previous post. For
consists of two copies of the unit interval, an upper one and a lower one. See the first two diagrams in this previous post. For 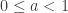 , a basic open set containing the point
, a basic open set containing the point  in the upper interval is of the form
in the upper interval is of the form 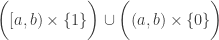 . For
. For 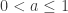 , a basic open set containing the point
, a basic open set containing the point  in the lower interval is of the form
in the lower interval is of the form ![\biggl( (c,a) \times \{ 1 \} \biggr) \cup \biggl( (c,a] \times \{0 \} \biggr)](https://s0.wp.com/latex.php?latex=%5Cbiggl%28+%28c%2Ca%29+%5Ctimes+%5C%7B+1+%5C%7D+%5Cbiggr%29+%5Ccup+%5Cbiggl%28+%28c%2Ca%5D+%5Ctimes+%5C%7B0+%5C%7D+%5Cbiggr%29&bg=ffffff&fg=333333&s=0&c=20201002) . The rightmost point in the upper interval
. The rightmost point in the upper interval  and the leftmost point in the lower interval
and the leftmost point in the lower interval 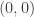 are made isolated points.
are made isolated points.
The double arrow space  is compact, perfectly normal and not metrizable (discussed here). Thus
is compact, perfectly normal and not metrizable (discussed here). Thus  does not have a
does not have a  -diagonal. We do not have a direct way of showing that it does not have a small diagonal. We rely on a result from [5], which says that every compact metrizably fibered space with a small diagonal is metrizable. In light of this result, we only need to show that the double arrow space
-diagonal. We do not have a direct way of showing that it does not have a small diagonal. We rely on a result from [5], which says that every compact metrizably fibered space with a small diagonal is metrizable. In light of this result, we only need to show that the double arrow space  is metrizably fibered. A space
is metrizably fibered. A space  is metrizably fibered if there is a continuous map from
is metrizably fibered if there is a continuous map from  onto some metrizable space
onto some metrizable space  such that each point inverse is metrizable.
such that each point inverse is metrizable.
Starting with the double arrow space  , let
, let ![f:D \rightarrow [0,1]](https://s0.wp.com/latex.php?latex=f%3AD+%5Crightarrow+%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) be defined by
be defined by 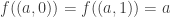 for each
for each 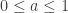 . This is a two-to-one continuous map from the double arrow space
. This is a two-to-one continuous map from the double arrow space  onto the unit interval. The map
onto the unit interval. The map  is essentially a quotient map, the result of identifying
is essentially a quotient map, the result of identifying 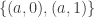 as one point
as one point  . By the result in [5], the double arrow space
. By the result in [5], the double arrow space  cannot have a small diagonal.
cannot have a small diagonal.
The Open Problem
As mentioned earlier, what makes the property of small diagonal is a related longstanding open problem. The statement “every compact space with a  -diagonal is metrizable” is true in ZFC. What about the following statement?
-diagonal is metrizable” is true in ZFC. What about the following statement?
(*) Every compact space with a small diagonal is metrizable.
This question whether this statement is true was raised in Husek [7]. As of the writing of this article, the problem is still unsolved. There are partial results, some consistent results and some ZFC results.
Assuming CH, the answer to Hesek’s question is positive. Husek [7] showed that under CH, every compact space  with a small diagonal such that the tightness of
with a small diagonal such that the tightness of  is countable is metrizable. Fact 3 from above states that every compact space with a small diagonal has countble tightness. Combining the two results, it follows that under CH any compact space with a small diagonal is metrizable. Fact 3 followed from a result by Juhasz and Szentmikloss [9]. Dow and Pavlov [3] showed that under PFA, every compact space with a small diagonal is metrizable.
is countable is metrizable. Fact 3 from above states that every compact space with a small diagonal has countble tightness. Combining the two results, it follows that under CH any compact space with a small diagonal is metrizable. Fact 3 followed from a result by Juhasz and Szentmikloss [9]. Dow and Pavlov [3] showed that under PFA, every compact space with a small diagonal is metrizable.
There are partial answers in ZFC. We mention three results. The first one is Fact 2 discussed above, which is that compact spaces with small diagonal are metrizable if there is a weight restriction (weight no more than  ). If there exists a non-metrizable compact space with a small diagonal, its weight would have to be greater than
). If there exists a non-metrizable compact space with a small diagonal, its weight would have to be greater than  .
.
Gruenhage [5] showed that every compact metrizably fibered space with a small diagonal is metrizable (this result is discussed in Example 3 above). Dow and Hart [2] showed that every compact space with a small diagonal that is weight  fibered is metrizable. The notion of weight
fibered is metrizable. The notion of weight  fibered is a generalization of metrizably fibered. A space
fibered is a generalization of metrizably fibered. A space  is weight
is weight  fibered if there is a continuous surjection
fibered if there is a continuous surjection 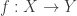 such that
such that  and each point inverse
and each point inverse 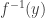 have weight at most
have weight at most  .
.
The statement “every countably compact space with a  -diagonal is metrizable” is a true statement in ZFC (see here). How about the statement “every countably compact space with a small diagonal is metrizable”, the statement (*) above with compact replaced by countably compact? Gruenhage [5] showed that this statement is consistent with and independent of ZFC. To prove or disprove this statement extra set theory assumptions beyond ZFC are required. This provides an interesting contrast between compact and countably compact with respect to the open problem. By broadening Husek’s question from compact to countably compact, the statement cannot be settled in ZFC. Dow and Pavlov [3] provided two consistent examples of “countably compact non-metrizable with small diagonal” that are improvements upon examples from Gruenhage.
-diagonal is metrizable” is a true statement in ZFC (see here). How about the statement “every countably compact space with a small diagonal is metrizable”, the statement (*) above with compact replaced by countably compact? Gruenhage [5] showed that this statement is consistent with and independent of ZFC. To prove or disprove this statement extra set theory assumptions beyond ZFC are required. This provides an interesting contrast between compact and countably compact with respect to the open problem. By broadening Husek’s question from compact to countably compact, the statement cannot be settled in ZFC. Dow and Pavlov [3] provided two consistent examples of “countably compact non-metrizable with small diagonal” that are improvements upon examples from Gruenhage.
Now consider the statement “Lindelof space with a small diagonal must have a  -diagonal.” Dow and Pavlov [3] provided a consistent negative answer, an example of a Lindelof space with a small diagonal that does not have a
-diagonal.” Dow and Pavlov [3] provided a consistent negative answer, an example of a Lindelof space with a small diagonal that does not have a  -diagonal (under negation of CH).
-diagonal (under negation of CH).
Another broad natural question is: what do compact spaces with small diagonal look like? The main problem is, of course, trying to see if these spaces are metrizable. There have been attempts to explore this general question of what these spaces look like. According to Juhasz and Szentmikloss [9], these spaces have countable tightness (Fact 2 above). However, it is not known if compact spaces with small diagonal have points of countable character. Dow and Hart [2] uncovered a surprising connection that if there is a subset of the real line that is a Luzin set, every compact space with a small diagonal does have points of countable character. Dow and Hart in the same paper also showed that in every compact space with a small diagonal, CCC subspaces have countable  -weight.
-weight.
This is a brief walk through of the open problem based on the statement (*) indicated above. To find out more, consult with the references listed below. Beyond the main open problem, there are many angles to be explored.
Reference
- Arhangelskii, A., Bella, A., Few observations on topological spaces with small diagonal, Zb. Rad. Filoz. Fak. Nisu, 6, No. 2, 211-213, 1992.
- Dow, A., Hart, P. Elementary chains and compact spaces with a small diagonal, Indagationes Mathematicae, 23, No. 3, 438-447, 2012.
- Dow, A., Pavlov, O. More about spaces with a small diagonal, Fund. Math., 191, No. 1, 67-80, 2006.
- Dow, A., Pavlov, O. Perfect preimages and small diagonal, Topology Proc., 31, No. 1, 89-95, 2007.
- Gruenhage, G., Spaces having a small diagonal, Topology Appl., 22, 183-200, 2002.
- Gruenhage, G., Generalized metrizable spaces, Recent Progress in General Topology III (K.P. Hart, J. van Mill, and P. Simon, eds.), Atlantis Press 2014.
- Husek, M., Topological spaces without
 -accessible diagonal, Comment. Math. Univ. Carolin., 18, No. 4, 777-788, 1977.
-accessible diagonal, Comment. Math. Univ. Carolin., 18, No. 4, 777-788, 1977.
- Juhasz, I., Cardinals Functions II, Handbook of Set-Theoretic Topology (K. Kunen and J. E. Vaughan, eds), Elsevier Science Publishers B. V., Amsterdam, 63-109, 1984.
- Juhasz, I., Szentmikloss, Z. Convergent free sequences in compact spaces, Proc. Amer. Math. Soc., 116, No. 4, 1153-1160, 1992.
- Zhou, H. X., On The Small Diagonals, Topology Appl., 13, 283-293, 1982.
Dan Ma topology
Daniel Ma topology
Dan Ma math
Daniel Ma mathematics
 2021 Dan Ma
2021 Dan Ma
be a mapping from a topological space
onto a topological space
. If
is a perfect map and
is a Lindelof space, then so is
. If
is a closed map and
is a paracompact space, then so is
. In other words, the pre-image of a Lindelof space under a perfect map is always a Lindelof space. Likewise, the pre-image of a paracompact space under a closed map is always a paracompact space. After proving these two facts, we show that for any compact space
, the product
is Lindelof (paracompact) for any Lindelof (paracompact) space
. All spaces under consideration are Hausdorff.
if the following holds: for any mapping
belonging to
, if
has the property, then so does
. In contrast, a topological property is an invariance of a class of mappings
if for any mapping
belonging to
, if
has the property, then so does
.
, where
, is a closed map if for any closed subset
of
,
is closed in
. A mapping
, where
, is a perfect map if
is a closed map and that the point inverse
is compact for each
.
be a closed map with
. Let
be an open subset of
. Define
. Then the set
is open in
and that
.
be a perfect map with
. Suppose
is Lindelof. Let
be an open cover of
. Without loss of generality, we can assume that
is closed under finite unions. For each
, define
. By Lemma 3, each
is an open subset of
. We claim that
is an open cover of
. To this end, let
. Since
is a perfect map, the point inverse
is compact. As a result, we can find a finite
such that
. Since
is closed under finite unions,
. It follows that
. Since
is Lindelof, there exists a countable
such that
. For each
,
for some
. We claim that
is a cover of
. To this end, let
. Then for some
,
. This implies that
. Thus, the open cover
has a countable subcover. This concludes the proof of Theorem 1.
be a perfect map with
. Suppose
is paracompact. Let
be an open cover of
. For each
, define
as in Lemma 3. By Lemma 3, each
is an open subset of
. Let
. As shown in the proof of Theorem 1,
is an open cover of
. Since
is paracompact, there exists a locally finite open refinement
of
. Let
.
. (1) It is an open cover of
. (2) It is a locally finite collection in
. (3) It is a refinement of
. To see (1), note that
is an open cover of
. As a result,
is an open cover of
. To see (2), let
. We find an open
such that
and such that
intersects only finitely many elements of
. Since
is locally finite in
, there exists an open
such that
and such that
intersects only finitely many elements of
, say,
. Let
. Clearly,
. It can be verified that the only elements of
having non-empty intersections with
are
,
,
. To see (3), let
where
. Then
for some
and some
. We claim that
. Let
. Then
. This implies that
. It follows that
is a locally finite open refinement of the open cover
. This completes the proof of Theorem 2.
is productively paramcompact if
is paracompact for every paracompact space
. The definition for productively Lindelof can be stated in a similar way. For some reason, the term “productively paracompact” is not used in the literature but is a topic that had been extensively studied. It is also a topic found in this site. The following four classes of spaces are productively paracompact (see here and here).
-compact spaces
-locally compact spaces
any compact space. Then
is Lindelof for every Lindelof space
.
any compact space. Then
is paracompact for every paracompact space
.
is compact. Then the projection map from
onto
is a closed map. The paracompactness of
follows whenever
is paracompact. The projection map is also perfect since the point inverses are compact due to the compactness of the factor
. Then the Lindelofness of
follows whenever
is Lindelof.
2023 – Dan Ma
