A little corner in the world of set-theoretic topology

Posted on October 15, 2018 by Dan Ma

This post puts a spot light on a little corner in the world of set-theoretic topology. There lies in this corner a simple topological statement that opens a door to the esoteric world of independence results. In this post, we give a proof of this basic fact and discuss its ramifications. This basic result is an excellent entry point to the study of S and L spaces.

The following paragraph is found in the paper called Gently killing S-spaces by Todd Eisworth, Peter Nyikos and Saharon Shelah [1]. The basic fact in question is highlighted in blue.

A simultaneous generalization of hereditarily separable and hereditarily Lindelof spaces is the class of spaces of countable spread – those spaces in which every discrete subspace is countable. One of the basic facts in this little corner of set-theoretic topology is that if a regular space of countable spread is not hereditarily separable, it contains an L-space, and if it is not hereditarily Lindelof, it contains an S-space. [1]

The same basic fact is also mentioned in the paper called The spread of regular spaces by Judith Roitman [2].

It is also well known that a regular space of countable spread which is not hereditarily separable contains an L-space and a regular space of countable spread which is not hereditarily Lindelof contains an S-space. Thus an absolute example of a space satisfying (Statement) A would contain a proof of the existence of S and L space – a consummation which some may devoutly wish, but which this paper does not attempt. [2]

Statement A in [2] is: There exists a 0-dimensional Hausdorff space of countable spread that is not the union of a hereditarily separable and a hereditarily Lindelof space. Statement A would mean the existence of a regular space of countable spread that is not hereditarily separable and that is also not hereditarily Lindelof. By the well known fact just mentioned, statement A would imply the existence of a space that is simultaneously an S-space and an L-space!

Let’s unpack the preceding section. First some basic definitions. A space $X$ is of countable spread (has countable spread) if every discrete subspace of $X$ is countable. A space $X$ is hereditarily separable if every subspace of $X$ is separable. A space $X$ is hereditarily Lindelof if every subspace of $X$ is Lindelof. A space is an S-space if it is hereditarily separable but not Lindelof. A space is an L-space if it is hereditarily Lindelof but not separable. See [3] for a basic discussion of S and L spaces.

Hereditarily separable but not Lindelof spaces as well as hereditarily Lindelof but not separable spaces can be easily defined in ZFC [3]. However, such examples are not regular. For the notions of S and L-spaces to be interesting, the definitions must include regularity. Thus in the discussion that follows, all spaces are assumed to be Hausdorff and regular.

One amazing aspect about set-theoretic topology is that one sometimes does not have to stray far from basic topological notions to encounter pathological objects such as S-spaces and L-spaces. The definition of a topological space is of course a basic definition. Separable spaces and Lindelof spaces are basic notions that are not far from the definition of topological spaces. The same can be said about hereditarily separable and hereditarily Lindelof spaces. Out of these basic ingredients come the notion of S-spaces and L-spaces, the existence of which is one of the key motivating questions in set-theoretic topology in the twentieth century. The study of S and L-spaces is a body of mathematics that had been developed for nearly a century. It is a fruitful area of research at the boundary of topology and axiomatic set theory.

The existence of an S-space is independent of ZFC (as a result of the work by Todorcevic in early 1980s). This means that there is a model of set theory in which an S-space exists and there is also a model of set theory in which S-spaces cannot exist. One half of the basic result mentioned in the preceding section is intimately tied to the existence of S-spaces and thus has interesting set-theoretic implications. The other half of the basic result involves the existence of L-spaces, which are shown to exist without using extra set theory axioms beyond ZFC by Justin Moore in 2005, which went against the common expectation that the existence of L-spaces would be independent of ZFC as well.

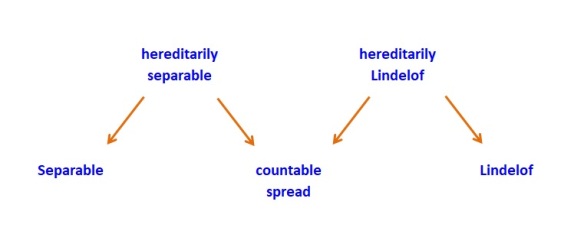
Let’s examine the basic notions in a little more details. The following diagram shows the properties surrounding the notion of countable spread.

Diagram 1 – Properties surrounding countable spread

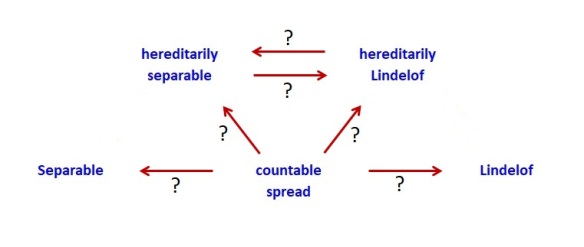
The implications (the arrows) in Diagram 1 can be verified easily. Central to the discussion at hand, both hereditarily separable and hereditarily Lindelof imply countable spread. The best way to see this is that if a space has an uncountable discrete subspace, that subspace is simultaneously a non-separable subspace and a non-Lindelof subspace. A natural question is whether these implications can be reversed. Another question is whether the properties in Diagram 1 can be related in other ways. The following diagram attempts to ask these questions.

Diagram 2 – Reverse implications surrounding countable spread

Not shown in Diagram 2 are these four facts: separable $\not \rightarrow$ hereditarily separable, Lindelof $\not \rightarrow$ hereditarily Lindelof, separable $\not \rightarrow$ countable spread and Lindelof $\not \rightarrow$ countable spread. The examples supporting these facts are not set-theoretic in nature and are not discussed here.

Let’s focus on each question mark in Diagram 2. The two horizontal arrows with question marks at the top are about S-space and L-space. If $X$ is hereditarily separable, then is $X$ hereditarily Lindelof? A “no” answer would mean there is an S-space. A “yes” answer would mean there exists no S-space. So the top arrow from left to right is independent of ZFC. Since an L-space can be constructed within ZFC, the question mark in the top arrow in Diagram 2 from right to left has a “no” answer.

Now focus on the arrows emanating from countable spread in Diagram 2. These arrows are about the basic fact discussed earlier. From Diagram 1, we know that hereditarily separable implies countable spread. Can the implication be reversed? Any L-space would be an example showing that the implication cannot be reversed. Note that any L-space is of countable spread and is not separable and hence not hereditarily separable. Since L-space exists in ZFC, the question mark in the arrow from countable spread to hereditarily separable has a “no” answer. The same is true for the question mark in the arrow from countable spread to separable

We know that hereditarily Lindelof implies countable spread. Can the implication be reversed? According to the basic fact mentioned earlier, if the implication cannot be reversed, there exists an S-space. Thus if S-space does not exist, the implication can be reversed. Any S-space is an example showing that the implication cannot be reversed. Thus the question in the arrow from countable spread to hereditarily Lindelof cannot be answered without assuming axioms beyond ZFC. The same is true for the question mark for the arrow from countable spread to Lindelf.

Diagram 2 is set-theoretic in nature. The diagram is remarkable in that the properties in the diagram are basic notions that are only brief steps away from the definition of a topological space. Thus the basic highlighted here is a quick route to the world of independence results.

We now give a proof of the basic result, which is stated in the following theorem.

Theorem 1
Let $X$ is regular and Hausdorff space. Then the following is true.

If $X$ is of countable spread and is not a hereditarily separable space, then $X$ contains an L-space.
If $X$ is of countable spread and is not a hereditarily Lindelof space, then $X$ contains an S-space.

To that end, we use the concepts of right separated space and left separated space. Recall that an initial segment of a well-ordered set $(X,<)$ is a set of the form $\{y \in X: y<x \}$ where $x \in X$ . A space $X$ is a right separated space if $X$ can be well-ordered in such a way that every initial segment is open. A right separated space is in type $\kappa$ if the well-ordering is of type $\kappa$ . A space $X$ is a left separated space if $X$ can be well-ordered in such a way that every initial segment is closed. A left separated space is in type $\kappa$ if the well-ordering is of type $\kappa$ . The following results are used in proving Theorem 1.

Theorem A
Let $X$ is regular and Hausdorff space. Then the following is true.

The space $X$ is hereditarily separable space if and only if $X$ has no uncountable left separated subspace.
The space $X$ is hereditarily Lindelof space if and only if $X$ has no uncountable right separated subspace.

Proof of Theorem A
$\Longrightarrow$ of the first bullet point.
Suppose $Y \subset X$ is an uncountable left separated subspace. Suppose that the well-ordering of $Y$ is of type $\kappa$ where $\kappa>\omega$ . Further suppose that $Y=\{ x_\alpha: \alpha<\kappa \}$ such that for each $\alpha<\kappa$ , $C_\alpha=\{ x_\beta: \beta<\alpha \}$ is a closed subset of $Y$ . Since $\kappa$ is uncountable, the well-ordering has an initial segment of type $\omega_1$ . So we might as well assume $\kappa=\omega_1$ . Note that for any countable $A \subset Y$ , $A \subset C_\alpha$ for some $\alpha<\omega_1$ . It follows that $Y$ is not separable. This means that $X$ is not hereditarily separable.

$\Longleftarrow$ of the first bullet point.
Suppose that $X$ is not hereditarily separable. Let $Y \subset X$ be a subspace that is not separable. We now inductively derive an uncountable left separated subspace of $Y$ . Choose $y_0 \in Y$ . For each $\alpha<\omega_1$ , let $A_\alpha=\{ y_\beta \in Y: \beta <\alpha \}$ . The set $A_\alpha$ is the set of all the points of $Y$ chosen before the step at $\alpha<\omega_1$ . Since $A_\alpha$ is countable, its closure in $Y$ is not the entire space $Y$ . Choose $y_\alpha \in Y-\overline{A_\alpha}=O_\alpha$ .

Let $Y_L=\{ y_\alpha: \alpha<\omega_1 \}$ . We claim that $Y_L$ is a left separated space. To this end, we need to show that each initial segment $A_\alpha$ is a closed subset of $Y_L$ . Note that for each $\gamma \ge \alpha$ , $O_\gamma=Y-\overline{A_\gamma}$ is an open subset of $Y$ with $y_\gamma \in O_\gamma$ such that $O_\gamma \cap \overline{A_\gamma}=\varnothing$ and thus $O_\gamma \cap \overline{A_\alpha}=\varnothing$ (closure in $Y$ ). Then $U_\gamma=O_\gamma \cap Y_L$ is an open subset of $Y_L$ containing $y_\gamma$ such that $U_\gamma \cap A_\alpha=\varnothing$ . It follows that $Y-A_\alpha$ is open in $Y_L$ and that $A_\alpha$ is a closed subset of $Y_L$ .

$\Longrightarrow$ of the second bullet point.
Suppose $Y \subset X$ is an uncountable right separated subspace. Suppose that the well-ordering of $Y$ is of type $\kappa$ where $\kappa>\omega$ . Further suppose that $Y=\{ x_\alpha: \alpha<\kappa \}$ such that for each $\alpha<\kappa$ , $U_\alpha=\{ x_\beta: \beta<\alpha \}$ is an open subset of $Y$ .

Since $\kappa$ is uncountable, the well-ordering has an initial segment of type $\omega_1$ . So we might as well assume $\kappa=\omega_1$ . Note that $\{ U_\alpha: \alpha<\omega_1 \}$ is an open cover of $Y$ that has no countable subcover. It follows that $Y$ is not Lindelof. This means that $X$ is not hereditarily Lindelof.

$\Longleftarrow$ of the second bullet point.
Suppose that $X$ is not hereditarily Lindelof. Let $Y \subset X$ be a subspace that is not Lindelof. Let $\mathcal{U}$ be an open cover of $Y$ that has no countable subcover. We now inductively derive a right separated subspace of $Y$ of type $\omega_1$ .

Choose $U_0 \in \mathcal{U}$ and choose $y_0 \in U_0$ . Choose $y_1 \in Y-U_0$ and choose $U_1 \in \mathcal{U}$ such that $y_1 \in U_1$ . Let $\alpha<\omega_1$ . Suppose that points $y_\beta$ and open sets $U_\beta$ , $\beta<\alpha$ , have been chosen such that $y_\beta \in Y-\bigcup_{\delta<\beta} U_\delta$ and $y_\beta \in U_\beta$ . The countably many chosen open sets $U_\beta$ , $\beta<\alpha$ , cannot cover $Y$ . Choose $y_\alpha \in Y-\bigcup_{\beta<\alpha} U_\beta$ . Choose $U_\alpha \in \mathcal{U}$ such that $y_\alpha \in U_\alpha$ .

Let $Y_R=\{ y_\alpha: \alpha<\omega_1 \}$ . It follows that $Y_R$ is a right separated space. Note that for each $\alpha<\omega_1$ , $\{ y_\beta: \beta<\alpha \} \subset \bigcup_{\beta<\alpha} U_\beta$ and the open set $\bigcup_{\beta<\alpha} U_\beta$ does not contain $y_\gamma$ for any $\gamma \ge \alpha$ . This means that the initial segment $\{ y_\beta: \beta<\alpha \}$ is open in $Y_L$ . $\square$

Lemma B
Let $X$ be a space that is a right separated space and also a left separated space based on the same well ordering. Then $X$ is a discrete space.

Proof of Lemma B
Let $X=\{ w_\alpha: \alpha<\kappa \}$ such that the well-ordering is given by the ordinals in the subscripts, i.e. $w_\beta<w_\gamma$ if and only if $\beta<\gamma$ . Suppose that $X$ with this well-ordering is both a right separated space and a left separated space. We claim that every point is a discrete point, i.e. $\{ x_\alpha \}$ is open for any $\alpha<\kappa$ .

To see this, fix $\alpha<\kappa$ . The initial segment $A_\alpha=\{ w_\beta: \beta<\alpha \}$ is closed in $X$ since $X$ is a left separated space. On the other hand, the initial segment $\{ w_\beta: \beta < \alpha+1 \}$ is open in $X$ since $X$ is a right separated space. Then $B_{\alpha}=\{ w_\beta: \beta \ge \alpha+1 \}$ is closed in $X$ . It follows that $\{ x_\alpha \}$ must be open since $X=A_\alpha \cup B_\alpha \cup \{ w_\alpha \}$ . $\square$

Theorem C
Let $X$ is regular and Hausdorff space. Then the following is true.

Suppose the space $X$ is right separated space of type $\omega_1$ . Then if $X$ has no uncountable discrete subspaces, then $X$ is an S-space or $X$ contains an S-space.
Suppose the space $X$ is left separated space of type $\omega_1$ . Then if $X$ has no uncountable discrete subspaces, then $X$ is an L-space or $X$ contains an L-space.

Proof of Theorem C
For the first bullet point, suppose the space $X$ is right separated space of type $\omega_1$ . Then by Theorem A, $X$ is not hereditarily Lindelof. If $X$ is hereditarily separable, then $X$ is an S-space (if $X$ is not Lindelof) or $X$ contains an S-space (a non-Lindelof subspace of $X$ ). Suppose $X$ is not hereditarily separable. By Theorem A, $X$ has an uncountable left separated subspace of type $\omega_1$ .

Let $X=\{ x_\alpha: \alpha<\omega_1 \}$ such that the well-ordering represented by the ordinals in the subscripts is a right separated space. Let $<_R$ be the symbol for the right separated well-ordering, i.e. $x_\beta <_R \ x_\delta$ if and only if $\beta<\delta$ . As indicated in the preceding paragraph, $X$ has an uncountable left separated subspace. Let $Y=\{ y_\alpha \in X: \alpha<\omega_1 \}$ be this left separated subspace. Let $<_L$ be the symbol for the left separated well-ordering. The well-ordering $<_R$ may be different from the well-ordering $<_L$ . However, we can obtain an uncountable subset of $Y$ such that the two well-orderings coincide on this subset.

To start, pick any $y_\gamma$ in $Y$ and relabel it $t_0$ . The final segment $\{y_\beta \in Y: t_0 <_L \ y_\beta \}$ must intersect the final segment $\{x_\beta \in X: t_0 <_R \ x_\beta \}$ in uncountably many points. Choose the least such point (according to $<_R$ ) and call it $t_1$ . It is clear how $t_{\delta+1}$ is chosen if $t_\delta$ has been chosen.

Suppose $\alpha<\omega_1$ is a limit ordinal and that $t_\beta$ has been chosen for all $\beta<\alpha$ . Then the set $\{y_\tau: \forall \ \beta<\alpha, t_\beta <_L \ y_\tau \}$ and the set $\{x_\tau: \forall \ \beta<\alpha, t_\beta <_R \ x_\tau \}$ must intersect in uncountably many points. Choose the least such point and call it $t_\alpha$ (according to $<_R$ ). As a result, we have obtained $T=\{ t_\alpha: \alpha<\omega_1 \}$ . It follows that T with the well-ordering represented by the ordinals in the subscript is a subset of $(X,<_R)$ and a subset of $(Y,<_L)$ . Thus $T$ is both right separated and left separated.

By Lemma B, $T$ is a discrete subspace of $X$ . However, $X$ is assumed to have no uncountable discrete subspace. Thus if $X$ has no uncountable discrete subspace, then $X$ must be hereditarily separable and as a result, must be an S-space or must contain an S-space.

The proof for the second bullet point is analogous to that of the first bullet point. $\square$

We are now ready to prove Theorem 1.

Proof of Theorem 1
Suppose that $X$ is of countable spread and that $X$ is not hereditarily separable. By Theorem A, $X$ has an uncountable left separated subspace $Y$ (assume it is of type $\omega_1$ ). The property of countable spread is hereditary. So $Y$ is of countable spread. By Theorem C, $Y$ is an L-space or $Y$ contains an L-space. In either way, $X$ contains an L-space.

Suppose that $X$ is of countable spread and that $X$ is not hereditarily Lindelof. By Theorem A, $X$ has an uncountable right separated subspace $Y$ (assume it is of type $\omega_1$ ). By Theorem C, $Y$ is an S-space or $Y$ contains an S-space. In either way, $X$ contains an S-space.

Reference

Eisworth T., Nyikos P., Shelah S., Gently killing S-spaces, Israel Journal of Mathmatics, 136, 189-220, 2003.
Roitman J., The spread of regular spaces, General Topology and Its Applications, 8, 85-91, 1978.
Roitman, J., Basic S and L, Handbook of Set-Theoretic Topology, (K. Kunen and J. E. Vaughan, eds), Elsevier Science Publishers B. V., Amsterdam, 295-326, 1984.
Tatch-Moore J., A solution to the L space problem, Journal of the American Mathematical Society, 19, 717-736, 2006.

$\text{ }$

Dan Ma math

Daniel Ma mathematics

$\copyright$ 2018 – Dan Ma

Equivalent conditions for hereditarily Lindelof spaces

Posted on May 3, 2014 by Dan Ma

A topological space $X$ is Lindelof if every open cover $X$ has a countable subcollection that also is a cover of $X$ . A topological space $X$ is hereditarily Lindelof if every subspace of $X$ , with respect to the subspace topology, is a Lindelof space. In this post, we prove a theorem that gives two equivalent conditions for the hereditarily Lindelof property. We consider the following theorem.

Theorem 1
Let $X$ be a topological space. The following conditions are equivalent.

The space $X$ is a hereditarily Lindelof space.
Every open subspace of $X$ is Lindelof.
For every uncountable subspace $Y$ of $X$ , there exists a point $y \in Y$ such that every open subset of $X$ containing $y$ contains uncountably many points of $Y$ .

This is an excellent exercise for the hereditarily Lindelof property and for transfinite induction (for one of the directions). The equivalence $1 \longleftrightarrow 3$ is the exercise 3.12.7(d) on page 224 of [1]. The equivalence of the 3 conditions of Theorem 1 is mentioned on page 182 (chapter d-8) of [2].

Proof of Theorem 1
The direction $1 \longrightarrow 2$ is immediate. The direction $2 \longrightarrow 3$ is straightforward.

$3 \longrightarrow 1$
We show $\text{not } 1 \longrightarrow \text{not } 3$ . Suppose $T$ is a non-Lindelof subspace of $X$ . Let $\mathcal{U}$ be an open cover of $T$ such that no countable subcollection of $\mathcal{U}$ can cover $T$ . By a transfinite inductive process, choose a set of points $\left\{t_\alpha \in T: \alpha < \omega_1 \right\}$ and a collection of open sets $\left\{U_\alpha \in \mathcal{U}: \alpha < \omega_1 \right\}$ such that for each $\alpha < \omega_1$ , $t_\alpha \in U_\alpha$ and $t_\alpha \notin \cup \left\{U_\beta: \beta<\alpha \right\}$ . The inductive process is possible since no countable subcollection of $\mathcal{U}$ can cover $T$ . Now let $Y=\left\{t_\alpha: \alpha<\omega_1 \right\}$ . Note that each $U_\alpha$ can at most contain countably many points of $Y$ , namely the points in $\left\{t_\beta: \beta \le \alpha \right\}$ .

For each $\alpha$ , let $V_\alpha$ be an open subset of $X$ such that $U_\alpha=V_\alpha \cap Y$ . We can now conclude: for every point $t_\alpha$ of $Y$ , there exists an open set $V_\alpha$ containing $t_\alpha$ such that $V_\alpha$ contains only countably many points of $Y$ . This is the negation of condition 3. $\blacksquare$

____________________________________________________________________

Remarks

Condition 3 indicates that every uncountable set has a certain special type of limit points. Let $p \in X$ . We say $p$ is a limit point of the set $Y \subset X$ if every open set containing $p$ contains a point of $Y$ different from $p$ . Being a limit point of $Y$ , we only know that each open set containing $p$ contain infinitely many points of $Y$ (assuming a $T_1$ space). Thus the limit points indicated in condition 3 are a special type of limit points. According to the terminology of [1], if $p$ is a limit point of $Y$ satisfying condition 3, then $p$ is said to be a condensation point of $Y$ . According to Theorem 1, existence of condensation point in every uncountable set is a strong topological property (being equivalent to the hereditarily property). It is easy to see that of condition 3 holds, all but countably many points of any uncountable set $Y$ is a condensation point of $Y$ .

In some situations, we may not need the full strength of condition 3. In such situations, the following corollary may be sufficient.

Corollary 2
If the space $X$ is hereditarily Lindelof, then every uncountable subspace $Y$ of $X$ contains one of its limit points.

As noted earlier, if every uncountable set contains one of its limits, then all but countably many points of any uncountable set are limit points. To contrast the hereditarily Lindelof property with the Lindelof property, consider the following theorem.

Theorem 3
If the space $X$ is Lindelof, then every uncountable subspace $Y$ of $X$ has a limit point.

The condition “every uncountable subspace $Y$ of $X$ has a limit point” has another name. When a space satisfies this condition, it is said to have countable extent. The ideas in Corollary 2 and Theorem 3 are also discussed in this previous post.

____________________________________________________________________

Reference

Engelking, R., General Topology, Revised and Completed edition, Heldermann Verlag, Berlin, 1989.
Hart, K. P., Nagata J. I., Vaughan, J. E., editors, Encyclopedia of General Topology, First Edition, Elsevier Science Publishers B. V, Amsterdam, 2003.

____________________________________________________________________

$\copyright \ 2014 \text{ by Dan Ma}$

Cp(X) where X is a separable metric space

Posted on April 3, 2014 by Dan Ma

Let $\tau$ be an uncountable cardinal. Let $\prod_{\alpha < \tau} \mathbb{R}=\mathbb{R}^{\tau}$ be the Cartesian product of $\tau$ many copies of the real line. This product space is not normal since it contains $\prod_{\alpha \in \omega_1} \omega=\omega^{\omega_1}$ as a closed subspace. However, there are dense subspaces of $\mathbb{R}^{\tau}$ are normal. For example, the $\Sigma$ -product of $\tau$ copies of the real line is normal, i.e., the subspace of $\mathbb{R}^{\tau}$ consisting of points which have at most countably many non-zero coordinates (see this post). In this post, we look for more normal spaces among the subspaces of $\mathbb{R}^{\tau}$ that are function spaces. In particular, we look at spaces of continuous real-valued functions defined on a separable metrizable space, i.e., the function space $C_p(X)$ where $X$ is a separable metrizable space.

For definitions of basic open sets and other background information on the function space $C_p(X)$ , see this previous post.

____________________________________________________________________

$C_p(X)$ when $X$ is a separable metric space

In the remainder of the post, $X$ denotes a separable metrizable space. Then, $C_p(X)$ is more than normal. The function space $C_p(X)$ has the following properties:

normal,
Lindelof (hence paracompact and collectionwise normal),
hereditarily Lindelof (hence hereditarily normal),
hereditarily separable,
perfectly normal.

All such properties stem from the fact that $C_p(X)$ has a countable network whenever $X$ is a separable metrizable space.

Let $L$ be a topological space. A collection $\mathcal{N}$ of subsets of $L$ is said to be a network for $L$ if for each $x \in L$ and for each open $O \subset L$ with $x \in O$ , there exists some $A \in \mathcal{N}$ such that $x \in A \subset O$ . A countable network is a network that has only countably many elements. The property of having a countable network is a very strong property, e.g., having all the properties listed above. For a basic discussion of this property, see this previous post and this previous post.

To define a countable network for $C_p(X)$ , let $\mathcal{B}$ be a countable base for the domain space $X$ . For each $B \subset \mathcal{B}$ and for any open interval $(a,b)$ in the real line with rational endpoints, consider the following set:

$[B,(a,b)]=\left\{f \in C(X): f(B) \subset (a,b) \right\}$

There are only countably many sets of the form $[B,(a,b)]$ . Let $\mathcal{N}$ be the collection of sets, each of which is the intersection of finitely many sets of the form $[B,(a,b)]$ . Then $\mathcal{N}$ is a network for the function space $C_p(X)$ . To see this, let $f \in O$ where $O=\bigcap_{x \in F} [x,O_x]$ is a basic open set in $C_p(X)$ where $F \subset X$ is finite and each $O_x$ is an open interval with rational endpoints. For each point $x \in F$ , choose $B_x \in \mathcal{B}$ with $x \in B_x$ such that $f(B_x) \subset O_x$ . Clearly $f \in \bigcap_{x \in F} \ [B_x,O_x]$ . It follows that $\bigcap_{x \in F} \ [B_x,O_x] \subset O$ .

Examples include $C_p(\mathbb{R})$ , $C_p([0,1])$ and $C_p(\mathbb{R}^\omega)$ . All three can be considered subspaces of the product space $\mathbb{R}^c$ where $c$ is the cardinality of the continuum. This is true for any separable metrizable $X$ . Note that any separable metrizable $X$ can be embedded in the product space $\mathbb{R}^\omega$ . The product space $\mathbb{R}^\omega$ has cardinality $c$ . Thus the cardinality of any separable metrizable space $X$ is at most continuum. So $C_p(X)$ is the subspace of a product space of $\le$ continuum many copies of the real lines, hence can be regarded as a subspace of $\mathbb{R}^c$ .

A space $L$ has countable extent if every closed and discrete subset of $L$ is countable. The $\Sigma$ -product $\Sigma_{\alpha \in A} X_\alpha$ of the separable metric spaces $\left\{X_\alpha: \alpha \in A \right\}$ is a dense and normal subspace of the product space $\prod_{\alpha \in A} X_\alpha$ . The normal space $\Sigma_{\alpha \in A} X_\alpha$ has countable extent (hence collectionwise normal). The examples of $C_p(X)$ discussed here are Lindelof and hence have countable extent. Many, though not all, dense normal subspaces of products of separable metric spaces have countable extent. For a dense normal subspace of a product of separable metric spaces, one interesting problem is to find out whether it has countable extent.

____________________________________________________________________

$\copyright \ 2014 \text{ by Dan Ma}$

Pixley-Roy hyperspaces

Posted on February 16, 2014 by Dan Ma

In this post, we introduce a class of hyperspaces called Pixley-Roy spaces. This is a well-known and well studied set of topological spaces. Our goal here is not to be comprehensive but rather to present some selected basic results to give a sense of what Pixley-Roy spaces are like.

A hyperspace refers to a space in which the points are subsets of a given “ground” space. There are more than one way to define a hyperspace. Pixley-Roy spaces were first described by Carl Pixley and Prabir Roy in 1969 (see [5]). In such a space, the points are the non-empty finite subsets of a given ground space. More precisely, let $X$ be a $T_1$ space (i.e. finite sets are closed). Let $\mathcal{F}[X]$ be the set of all non-empty finite subsets of $X$ . For each $F \in \mathcal{F}[X]$ and for each open subset $U$ of $X$ with $F \subset U$ , we define:

$[F,U]=\left\{B \in \mathcal{F}[X]: F \subset B \subset U \right\}$

The sets $[F,U]$ over all possible $F$ and $U$ form a base for a topology on $\mathcal{F}[X]$ . This topology is called the Pixley-Roy topology (or Pixley-Roy hyperspace topology). The set $\mathcal{F}[X]$ with this topology is called a Pixley-Roy space.

The hyperspace as defined above was first defined by Pixley and Roy on the real line (see [5]) and was later generalized by van Douwen (see [7]). These spaces are easy to define and is useful for constructing various kinds of counterexamples. Pixley-Roy played an important part in answering the normal Moore space conjecture. Pixley-Roy spaces have also been studied in their own right. Over the years, many authors have investigated when the Pixley-Roy spaces are metrizable, normal, collectionwise Hausdorff, CCC and homogeneous. For a small sample of such investigations, see the references listed at the end of the post. Our goal here is not to discuss the results in these references. Instead, we discuss some basic properties of Pixley-Roy to solidify the definition as well as to give a sense of what these spaces are like. Good survey articles of Pixley-Roy are [3] and [7].

____________________________________________________________________

Basic Discussion

In this section, we focus on properties that are always possessed by a Pixley-Roy space given that the ground space is at least $T_1$ . Let $X$ be a $T_1$ space. We discuss the following points:

The topology defined above is a legitimate one, i.e., the sets $[F,U]$ indeed form a base for a topology on $\mathcal{F}[X]$ .
$\mathcal{F}[X]$ is a Hausdorff space.
$\mathcal{F}[X]$ is a zero-dimensional space.
$\mathcal{F}[X]$ is a completely regular space.
$\mathcal{F}[X]$ is a hereditarily metacompact space.

Let $\mathcal{B}=\left\{[F,U]: F \in \mathcal{F}[X] \text{ and } U \text{ is open in } X \right\}$ . Note that every finite set $F$ belongs to at least one set in $\mathcal{B}$ , namely $[F,X]$ . So $\mathcal{B}$ is a cover of $\mathcal{F}[X]$ . For $A \in [F_1,U_1] \cap [F_2,U_2]$ , we have $A \in [A,U_1 \cap U_2] \subset [F_1,U_1] \cap [F_2,U_2]$ . So $\mathcal{B}$ is indeed a base for a topology on $\mathcal{F}[X]$ .

To show $\mathcal{F}[X]$ is Hausdorff, let $A$ and $B$ be finite subsets of $X$ where $A \ne B$ . Then one of the two sets has a point that is not in the other one. Assume we have $x \in A-B$ . Since $X$ is $T_1$ , we can find open sets $U, V \subset X$ such that $x \in U$ , $x \notin V$ and $A \cup B-\left\{ x \right\} \subset V$ . Then $[A,U \cup V]$ and $[B,V]$ are disjoint open sets containing $A$ and $B$ respectively.

To see that $\mathcal{F}[X]$ is a zero-dimensional space, we show that $\mathcal{B}$ is a base consisting of closed and open sets. To see that $[F,U]$ is closed, let $C \notin [F,U]$ . Either $F \not \subset C$ or $C \not \subset U$ . In either case, we can choose open $V \subset X$ with $C \subset V$ such that $[C,V] \cap [F,U]=\varnothing$ .

The fact that $\mathcal{F}[X]$ is completely regular follows from the fact that it is zero-dimensional.

To show that $\mathcal{F}[X]$ is metacompact, let $\mathcal{G}$ be an open cover of $\mathcal{F}[X]$ . For each $F \in \mathcal{F}[X]$ , choose $G_F \in \mathcal{G}$ such that $F \in G_F$ and let $V_F=[F,X] \cap G_F$ . Then $\mathcal{V}=\left\{V_F: F \in \mathcal{F}[X] \right\}$ is a point-finite open refinement of $\mathcal{G}$ . For each $A \in \mathcal{F}[X]$ , $A$ can only possibly belong to $V_F$ for the finitely many $F \subset A$ .

A similar argument show that $\mathcal{F}[X]$ is hereditarily metacompact. Let $Y \subset \mathcal{F}[X]$ . Let $\mathcal{H}$ be an open cover of $Y$ . For each $F \in Y$ , choose $H_F \in \mathcal{H}$ such that $F \in H_F$ and let $W_F=([F,X] \cap Y) \cap H_F$ . Then $\mathcal{W}=\left\{W_F: F \in Y \right\}$ is a point-finite open refinement of $\mathcal{H}$ . For each $A \in Y$ , $A$ can only possibly belong to $W_F$ for the finitely many $F \subset A$ such that $F \in Y$ .

____________________________________________________________________

More Basic Results

We now discuss various basic topological properties of $\mathcal{F}[X]$ . We first note that $\mathcal{F}[X]$ is a discrete space if and only if the ground space $X$ is discrete. Though we do not need to make this explicit, it makes sense to focus on non-discrete spaces $X$ when we look at topological properties of $\mathcal{F}[X]$ . We discuss the following points:

If $X$ is uncountable, then $\mathcal{F}[X]$ is not separable.
If $X$ is uncountable, then every uncountable subspace of $\mathcal{F}[X]$ is not separable.
If $\mathcal{F}[X]$ is Lindelof, then $X$ is countable.
If $\mathcal{F}[X]$ is Baire space, then $X$ is discrete.
If $\mathcal{F}[X]$ has the CCC, then $X$ has the CCC.
If $\mathcal{F}[X]$ has the CCC, then $X$ has no uncountable discrete subspaces,i.e., $X$ has countable spread, which of course implies CCC.
If $\mathcal{F}[X]$ has the CCC, then $X$ is hereditarily Lindelof.
If $\mathcal{F}[X]$ has the CCC, then $X$ is hereditarily separable.
If $X$ has a countable network, then $\mathcal{F}[X]$ has the CCC.
The Pixley-Roy space of the Sorgenfrey line does not have the CCC.
If $X$ is a first countable space, then $\mathcal{F}[X]$ is a Moore space.

Bullet points 6 to 9 refer to properties that are never possessed by Pixley-Roy spaces except in trivial cases. Bullet points 6 to 8 indicate that $\mathcal{F}[X]$ can never be separable and Lindelof as long as the ground space $X$ is uncountable. Note that $\mathcal{F}[X]$ is discrete if and only if $X$ is discrete. Bullet point 9 indicates that any non-discrete $\mathcal{F}[X]$ can never be a Baire space. Bullet points 10 to 13 give some necessary conditions for $\mathcal{F}[X]$ to be CCC. Bullet 14 gives a sufficient condition for $\mathcal{F}[X]$ to have the CCC. Bullet 15 indicates that the hereditary separability and the hereditary Lindelof property are not sufficient conditions for the CCC of Pixley-Roy space (though they are necessary conditions). Bullet 16 indicates that the first countability of the ground space is a strong condition, making $\mathcal{F}[X]$ a Moore space.

__________________________________

To see bullet point 6, let $X$ be an uncountable space. Let $\left\{F_1,F_2,F_3,\cdots \right\}$ be any countable subset of $\mathcal{F}[X]$ . Choose a point $x \in X$ that is not in any $F_n$ . Then none of the sets $F_i$ belongs to the basic open set $[\left\{x \right\} ,X]$ . Thus $\mathcal{F}[X]$ can never be separable if $X$ is uncountable.

__________________________________

To see bullet point 7, let $Y \subset \mathcal{F}[X]$ be uncountable. Let $W=\cup \left\{F: F \in Y \right\}$ . Let $\left\{F_1,F_2,F_3,\cdots \right\}$ be any countable subset of $Y$ . We can choose a point $x \in W$ that is not in any $F_n$ . Choose some $A \in Y$ such that $x \in A$ . Then none of the sets $F_n$ belongs to the open set $[A ,X] \cap Y$ . So not only $\mathcal{F}[X]$ is not separable, no uncountable subset of $\mathcal{F}[X]$ is separable if $X$ is uncountable.

__________________________________

To see bullet point 8, note that $\mathcal{F}[X]$ has no countable open cover consisting of basic open sets, assuming that $X$ is uncountable. Consider the open collection $\left\{[F_1,U_1],[F_2,U_2],[F_3,U_3],\cdots \right\}$ . Choose $x \in X$ that is not in any of the sets $F_n$ . Then $\left\{ x \right\}$ cannot belong to $[F_n,U_n]$ for any $n$ . Thus $\mathcal{F}[X]$ can never be Lindelof if $X$ is uncountable.

__________________________________

For an elementary discussion on Baire spaces, see this previous post.

To see bullet point 9, let $X$ be a non-discrete space. To show $\mathcal{F}[X]$ is not Baire, we produce an open subset that is of first category (i.e. the union of countably many closed nowhere dense sets). Let $x \in X$ a limit point (i.e. an non-isolated point). We claim that the basic open set $V=[\left\{ x \right\},X]$ is a desired open set. Note that $V=\bigcup \limits_{n=1}^\infty H_n$ where

$H_n=\left\{F \in \mathcal{F}[X]: x \in F \text{ and } \lvert F \lvert \le n \right\}$

We show that each $H_n$ is closed and nowhere dense in the open subspace $V$ . To see that it is closed, let $A \notin H_n$ with $x \in A$ . We have $\lvert A \lvert>n$ . Then $[A,X]$ is open and every point of $[A,X]$ has more than $n$ points of the space $X$ . To see that $H_n$ is nowhere dense in $V$ , let $[B,U]$ be open with $[B,U] \subset V$ . It is clear that $x \in B \subset U$ where $U$ is open in the ground space $X$ . Since the point $x$ is not an isolated point in the space $X$ , $U$ contains infinitely many points of $X$ . So choose an finite set $C$ with at least $2 \times n$ points such that $B \subset C \subset U$ . For the the open set $[C,U]$ , we have $[C,U] \subset [B,U]$ and $[C,U]$ contains no point of $H_n$ . With the open set $V$ being a union of countably many closed and nowhere dense sets in $V$ , the open set $V$ is not of second category. We complete the proof that $\mathcal{F}[X]$ is not a Baire space.

__________________________________

To see bullet point 10, let $\mathcal{O}$ be an uncountable and pairwise disjoint collection of open subsets of $X$ . For each $O \in \mathcal{O}$ , choose a point $x_O \in O$ . Then $\left\{[\left\{ x_O \right\},O]: O \in \mathcal{O} \right\}$ is an uncountable and pairwise disjoint collection of open subsets of $\mathcal{F}[X]$ . Thus if $\mathcal{F}[X]$ is CCC then $X$ must have the CCC.

__________________________________

To see bullet point 11, let $Y \subset X$ be uncountable such that $Y$ as a space is discrete. This means that for each $y \in Y$ , there exists an open $O_y \subset X$ such that $y \in O_y$ and $O_y$ contains no point of $Y$ other than $y$ . Then $\left\{[\left\{y \right\},O_y]: y \in Y \right\}$ is an uncountable and pairwise disjoint collection of open subsets of $\mathcal{F}[X]$ . Thus if $\mathcal{F}[X]$ has the CCC, then the ground space $X$ has no uncountable discrete subspace (such a space is said to have countable spread).

__________________________________

To see bullet point 12, let $Y \subset X$ be uncountable such that $Y$ is not Lindelof. Then there exists an open cover $\mathcal{U}$ of $Y$ such that no countable subcollection of $\mathcal{U}$ can cover $Y$ . We can assume that sets in $\mathcal{U}$ are open subsets of $X$ . Also by considering a subcollection of $\mathcal{U}$ if necessary, we can assume that cardinality of $\mathcal{U}$ is $\aleph_1$ or $\omega_1$ . Now by doing a transfinite induction we can choose the following sequence of points and the following sequence of open sets:

$\left\{x_\alpha \in Y: \alpha < \omega_1 \right\}$

$\left\{U_\alpha \in \mathcal{U}: \alpha < \omega_1 \right\}$

such that $x_\beta \ne x_\gamma$ if $\beta \ne \gamma$ , $x_\alpha \in U_\alpha$ and $x_\alpha \notin \bigcup \limits_{\beta < \alpha} U_\beta$ for each $\alpha < \omega_1$ . At each step $\alpha$ , all the previously chosen open sets cannot cover $Y$ . So we can always choose another point $x_\alpha$ of $Y$ and then choose an open set in $\mathcal{U}$ that contains $x_\alpha$ .

Then $\left\{[\left\{x_\alpha \right\},U_\alpha]: \alpha < \omega_1 \right\}$ is a pairwise disjoint collection of open subsets of $\mathcal{F}[X]$ . Thus if $\mathcal{F}[X]$ has the CCC, then $X$ must be hereditarily Lindelof.

__________________________________

To see bullet point 13, let $Y \subset X$ . Consider open sets $[A,U]$ where $A$ ranges over all finite subsets of $Y$ and $U$ ranges over all open subsets of $X$ with $A \subset U$ . Let $\mathcal{G}$ be a collection of such $[A,U]$ such that $\mathcal{G}$ is pairwise disjoint and $\mathcal{G}$ is maximal (i.e. by adding one more open set, the collection will no longer be pairwise disjoint). We can apply a Zorn lemma argument to obtain such a maximal collection. Let $D$ be the following subset of $Y$ .

$D=\bigcup \left\{A: [A,U] \in \mathcal{G} \text{ for some open } U \right\}$

We claim that the set $D$ is dense in $Y$ . Suppose that there is some open set $W \subset X$ such that $W \cap Y \ne \varnothing$ and $W \cap D=\varnothing$ . Let $y \in W \cap Y$ . Then $[\left\{y \right\},W] \cap [A,U]=\varnothing$ for all $[A,U] \in \mathcal{G}$ . So adding $[\left\{y \right\},W]$ to $\mathcal{G}$ , we still get a pairwise disjoint collection of open sets, contradicting that $\mathcal{G}$ is maximal. So $D$ is dense in $Y$ .

If $\mathcal{F}[X]$ has the CCC, then $\mathcal{G}$ is countable and $D$ is a countable dense subset of $Y$ . Thus if $\mathcal{F}[X]$ has the CCC, the ground space $X$ is hereditarily separable.

__________________________________

A collection $\mathcal{N}$ of subsets of a space $Y$ is said to be a network for the space $Y$ if any non-empty open subset of $Y$ is the union of elements of $\mathcal{N}$ , equivalently, for each $y \in Y$ and for each open $U \subset Y$ with $y \in U$ , there is some $A \in \mathcal{N}$ with $x \in A \subset U$ . Note that a network works like a base but the elements of a network do not have to be open. The concept of network and spaces with countable network are discussed in these previous posts Network Weight of Topological Spaces – I and Network Weight of Topological Spaces – II.

To see bullet point 14, let $\mathcal{N}$ be a network for the ground space $X$ such that $\mathcal{N}$ is also countable. Assume that $\mathcal{N}$ is closed under finite unions (for example, adding all the finite unions if necessary). Let $\left\{[A_\alpha,U_\alpha]: \alpha < \omega_1 \right\}$ be a collection of basic open sets in $\mathcal{F}[X]$ . Then for each $\alpha$ , find $B_\alpha \in \mathcal{N}$ such that $A_\alpha \subset B_\alpha \subset U_\alpha$ . Since $\mathcal{N}$ is countable, there is some $B \in \mathcal{N}$ such that $M=\left\{\alpha< \omega_1: B=B_\alpha \right\}$ is uncountable. It follows that for any finite $E \subset M$ , $\bigcap \limits_{\alpha \in E} [A_\alpha,U_\alpha] \ne \varnothing$ .

Thus if the ground space $X$ has a countable network, then $\mathcal{F}[X]$ has the CCC.

__________________________________

The implications in bullet points 12 and 13 cannot be reversed. Hereditarily Lindelof property and hereditarily separability are not sufficient conditions for $\mathcal{F}[X]$ to have the CCC. See [4] for a study of the CCC property of the Pixley-Roy spaces.

To see bullet point 15, let $S$ be the Sorgenfrey line, i.e. the real line $\mathbb{R}$ with the topology generated by the half closed intervals of the form $[a,b)$ . For each $x \in S$ , let $U_x=[x,x+1)$ . Then $\left\{[ \left\{ x \right\},U_x]: x \in S \right\}$ is a collection of pairwise disjoint open sets in $\mathcal{F}[S]$ .

__________________________________

A Moore space is a space with a development. For the definition, see this previous post.

To see bullet point 16, for each $x \in X$ , let $\left\{B_n(x): n=1,2,3,\cdots \right\}$ be a decreasing local base at $x$ . We define a development for the space $\mathcal{F}[X]$ .

For each finite $F \subset X$ and for each $n$ , let $B_n(F)=\bigcup \limits_{x \in F} B_n(x)$ . Clearly, the sets $B_n(F)$ form a decreasing local base at the finite set $F$ . For each $n$ , let $\mathcal{H}_n$ be the following collection:

$\mathcal{H}_n=\left\{[F,B_n(F)]: F \in \mathcal{F}[X] \right\}$

We claim that $\left\{\mathcal{H}_n: n=1,2,3,\cdots \right\}$ is a development for $\mathcal{F}[X]$ . To this end, let $V$ be open in $\mathcal{F}[X]$ with $F \in V$ . If we make $n$ large enough, we have $[F,B_n(F)] \subset V$ .

For each non-empty proper $G \subset F$ , choose an integer $f(G)$ such that $[F,B_{f(G)}(F)] \subset V$ and $F \not \subset B_{f(G)}(G)$ . Let $m$ be defined by:

$m=\text{max} \left\{f(G): G \ne \varnothing \text{ and } G \subset F \text{ and } G \text{ is proper} \right\}$

We have $F \not \subset B_{m}(G)$ for all non-empty proper $G \subset F$ . Thus $F \notin [G,B_m(G)]$ for all non-empty proper $G \subset F$ . But in $\mathcal{H}_m$ , the only sets that contain $F$ are $[F,B_m(F)]$ and $[G,B_m(G)]$ for all non-empty proper $G \subset F$ . So $[F,B_m(F)]$ is the only set in $\mathcal{H}_m$ that contains $F$ , and clearly $[F,B_m(F)] \subset V$ .

We have shown that for each open $V$ in $\mathcal{F}[X]$ with $F \in V$ , there exists an $m$ such that any open set in $\mathcal{H}_m$ that contains $F$ must be a subset of $V$ . This shows that the $\mathcal{H}_n$ defined above form a development for $\mathcal{F}[X]$ .

____________________________________________________________________

Examples

In the original construction of Pixley and Roy, the example was $\mathcal{F}[\mathbb{R}]$ . Based on the above discussion, $\mathcal{F}[\mathbb{R}]$ is a non-separable CCC Moore space. Because the density (greater than $\omega$ for not separable) and the cellularity ( $=\omega$ for CCC) do not agree, $\mathcal{F}[\mathbb{R}]$ is not metrizable. In fact, it does not even have a dense metrizable subspace. Note that countable subspaces of $\mathcal{F}[\mathbb{R}]$ are metrizable but are not dense. Any uncountable dense subspace of $\mathcal{F}[\mathbb{R}]$ is not separable but has the CCC. Not only $\mathcal{F}[\mathbb{R}]$ is not metrizable, it is not normal. The problem of finding $X \subset \mathbb{R}$ for which $\mathcal{F}[X]$ is normal requires extra set-theoretic axioms beyond ZFC (see [6]). In fact, Pixley-Roy spaces played a large role in the normal Moore space conjecture. Assuming some extra set theory beyond ZFC, there is a subset $M \subset \mathbb{R}$ such that $\mathcal{F}[M]$ is a CCC metacompact normal Moore space that is not metrizable (see Example I in [8]).

On the other hand, Pixley-Roy space of the Sorgenfrey line and the Pixley-Roy space of $\omega_1$ (the first uncountable ordinal with the order topology) are metrizable (see [3]).

The Sorgenfrey line and the first uncountable ordinal are classic examples of topological spaces that demonstrate that topological spaces in general are not as well behaved like metrizable spaces. Yet their Pixley-Roy spaces are nice. The real line and other separable metric spaces are nice spaces that behave well. Yet their Pixley-Roy spaces are very much unlike the ground spaces. This inverse relation between the ground space and the Pixley-Roy space was noted by van Douwen (see [3] and [7]) and is one reason that Pixley-Roy hyperspaces are a good source of counterexamples.

____________________________________________________________________

Reference

Bennett, H. R., Fleissner, W. G., Lutzer, D. J., Metrizability of certain Pixley-Roy spaces, Fund. Math. 110, 51-61, 1980.
Daniels, P, Pixley-Roy Spaces Over Subsets of the Reals, Topology Appl. 29, 93-106, 1988.
Lutzer, D. J., Pixley-Roy topology, Topology Proc. 3, 139-158, 1978.
Hajnal, A., Juahasz, I., When is a Pixley-Roy Hyperspace CCC?, Topology Appl. 13, 33-41, 1982.
Pixley, C., Roy, P., Uncompletable Moore spaces, Proc. Auburn Univ. Conf. Auburn, AL, 1969.
Przymusinski, T., Normality and paracompactness of Pixley-Roy hyperspaces, Fund. Math. 113, 291-297, 1981.
van Douwen, E. K., The Pixley-Roy topology on spaces of subsets, Set-theoretic Topology, Academic Press, New York, 111-134, 1977.
Tall, F. D., Normality versus Collectionwise Normality, Handbook of Set-Theoretic Topology (K. Kunen and J. E. Vaughan, eds), Elsevier Science Publishers B. V., Amsterdam, 685-732, 1984.
Tanaka, H, Normality and hereditary countable paracompactness of Pixley-Roy hyperspaces, Fund. Math. 126, 201-208, 1986.

____________________________________________________________________

$\copyright \ 2014 \text{ by Dan Ma}$

Cartesian Products of Two Paracompact Spaces – Continued

Posted on November 11, 2012 by Dan Ma

Consider the real line $\mathbb{R}$ with a topology finer than the usual topology obtained by isolating each point in $\mathbb{P}$ where $\mathbb{P}$ is the set of all irrational numbers. The real line with this finer topology is called the Michael line and we use $\mathbb{M}$ to denote this topological space. It is a classic result that $\mathbb{M} \times \mathbb{P}$ is not normal (see “Michael Line Basics”). Even though the Michael line $\mathbb{M}$ is paracompact (it is in fact hereditarily paracompact), $\mathbb{M}$ is not perfectly normal. Result 3 below will imply that the Michael line cannot be perfectly normal. Otherwise $\mathbb{M} \times \mathbb{P}$ would be paracompact (hence normal). Result 3 is the statement that if $X$ is paracompact and perfectly normal and Y is a metric space then $X \times Y$ is paracompact and perfectly normal. We also use this result to show that if $X$ is hereditarily Lindelof and $Y$ is a separable metric space, then $X \times Y$ is hereditarily Lindelof (see Result 4 below).

This post is a continuation of the post “Cartesian Products of Two Paracompact Spaces”. In that post, four results are listed. They are:

Result 1

$X$

$Y$

$X \times Y$

Result 2

$X$

$Y$

$\sigma$

$X \times Y$

Result 3

$X$

$Y$

$X \times Y$

Result 4

$X$

$Y$

$X \times Y$

Result 1 and Result 2 are proved in the previous post “Cartesian Products of Two Paracompact Spaces”. Result 3 and Result 4 are proved in this post. All spaces are assumed to be regular.

___________________________________________________________________________________

Paracompact Spaces, Lindelof Spaces and Other Information

A paracompact space is one in which every open cover has a locally finite open refinement. The previous post “Cartesian Products of Two Paracompact Spaces” has a basic discussion on paracompact spaces. For the sake of completeness, we repeat here some of the results discussed in that post. A proof of Proposition 1 can be found in [1] (Theorem 5.1.11 in page 302) or in [2] (Theorem 20.7 in page 146).. For a proof of Proposition 2, see Theorem 3 in the previous post “Cartesian Products of Two Paracompact Spaces”. We provide a proof for Proposition 3.

Proposition 1
Let $X$ be a regular space. Then $X$ is paracompact if and only if every open cover $\mathcal{U}$ of $X$ has a $\sigma$ -locally finite open refinement.

Proposition 2
Every $F_\sigma$ -subset of a paracompact space is paracompact.

Proposition 3
Any paracompact space with a dense Lindelof subspace is Lindelof.

Proof of Proposition 3
Let $L$ be a paracompact space. Let $M \subset L$ be a dense Lindelof subspace. Let $\mathcal{U}$ be an open cover of $L$ . Since we are working with a regular space, let $\mathcal{V}$ be an open cover of $L$ such that $\left\{\overline{V}: V \in \mathcal{V} \right\}$ refines $\mathcal{U}$ . Let $\mathcal{W}$ be a locally finite open refinement of $\mathcal{V}$ . Choose $\left\{W_1,W_2,W_3,\cdots \right\} \subset \mathcal{W}$ such that it is a cover of $M$ . Since $M \subset \bigcup \limits_{i=1}^\infty W_i$ , $\overline{\bigcup \limits_{i=1}^\infty W_i}=L$ .

Since the sets $W_i$ come from a locally finite collection, they are closure preserving. Hence we have:

$\overline{\bigcup \limits_{i=1}^\infty W_i}=\bigcup \limits_{i=1}^\infty \overline{W_i}=L$

For each $i$ , choose some $U_i \in \mathcal{U}$ such that $\overline{W_i} \subset U_i$ . Then $\left\{U_1,U_2,U_3,\cdots \right\}$ is a countable subcollection of $\mathcal{U}$ covering the space $L$ . $\blacksquare$

A space is said to be a perfectly normal if it is a normal space with the additional property that every closed subset is a $G_\delta$ -set in the space (equivalently every open subset is an $F_\sigma$ -set). We need two basic results about hereditarily Lindelof spaces. A space is Lindelof if every open cover of that space has a countable subcover. A space is hereditarily Lindelof if every subspace of that space is Lindelof. Proposition 4 below, stated without proof, shows that to prove a space is hereditarily Lindelof, we only need to show that every open subspace is Lindelof.

Proposition 4
Let $L$ be a space. Then $L$ is hereditarily Lindelof if and only if every open subspace of $L$ is Lindelof.

Proposition 5
Let $L$ be a Lindelof space. Then $L$ is hereditarily Lindelof if and only if $L$ is perfectly normal.

Proof of Proposition 5
$\Rightarrow$ Suppose $L$ is hereditarily Lindelof. It is well known that regular Lindelof space is normal. Thus $L$ is normal. It remains to show that every open subset of $L$ is $F_\sigma$ . Let $U \subset L$ be an non-empty open set. For each $x \in U$ , let $V_x$ be open such that $x \in V_x$ and $\overline{V_x} \subset U$ (the space is assumed to be regular). By assumption, the open set $U$ is Lindelof. The open sets $V_x$ form an open cover of $U$ . Thus $U$ is the union of countably many $\overline{V}_x$ .

$\Leftarrow$ Suppose $L$ is perfectly normal. To show that $L$ is hereditarily Lindelof, it suffices to show that every open subset of $L$ is Lindelof (by Proposition 4). Let $U \subset L$ be non-empty open. By assumption, $U=\bigcup \limits_{i=1}^\infty F_i$ where each $F_i$ is a closed set in $L$ . Since the Lindelof property is hereditary with respect to closed subsets, $U$ is Lindelof. $\blacksquare$

Another important piece of information that we need is the following metrization theorem. It shows that being a metrizable space is equivalent to have a base that is $\sigma$ -locally finite. In proving Result 3, we will assume that the metric factor has such a base. This is a classic metrization theorem (see [1] or [2] or any other standard topology text).

Theorem 6
Let $X$ be a space. Then $X$ is metrizable if and only if $X$ has a $\sigma$ -locally finite base.

___________________________________________________________________________________

Result 3

Result 3 is the statement that:

$X$

$X \times Y$

Result 3 follows from the following two lemmas.

Lemma 7
If the following two conditions hold:

every open subset of $X$ is an $F_\sigma$ -set in $X$ ,
$Y$ is a metric space,

then every open subset of $X \times Y$ is an $F_\sigma$ -set in $X \times Y$ .

Proof of Lemma 7
Let $U$ be a open subset of $X \times Y$ . If $U=\varnothing$ , then $U$ is certainly the union of countably many closed sets. So assume $U \ne \varnothing$ . Let $\mathcal{B}=\bigcup \limits_{i=1}^\infty \mathcal{B}_i$ be a base for $Y$ such that each $\mathcal{B}_i$ is locally finite in $Y$ (by Theorem 6, such a base exists since $Y$ is metrizable).

Consider all non-empty $B \in \mathcal{B}$ such that we can choose nonempty open set $W_B \subset X$ with $W_B \times \overline{B} \subset U$ . Since $U$ is non-empty open, such pairs $(B, W_B)$ exist. Let $\mathcal{B}^*$ be the collection of all non-empty $B \in \mathcal{B}$ for which there is a matching non-empty $W_B$ . For each $i$ , let $\mathcal{B}_i^*=\mathcal{B}^* \cap \mathcal{B}_i$ . Of course, each $\mathcal{B}_i^*$ is still locally finite.

Since every open subset of $X$ is an $F_\sigma$ -set in $X$ , for each $W_B$ , we can write $W_B$ as

$W_B=\bigcup \limits_{j=1}^\infty W_{B,j}$

where each $W_{B,i}$ is closed in $X$ .

For each $i=1,2,3,\cdots$ and each $j=1,2,3,\cdots$ , consider the following collection:

$\mathcal{V}_{i,j}=\left\{W_{B,j} \times \overline{B}: B \in \mathcal{B}_i^* \right\}$

Each element of $\mathcal{V}_{i,j}$ is a closed set in $X \times Y$ . Since $\mathcal{B}_i^*$ is a locally finite collection in $Y$ , $\mathcal{V}_{i,j}$ is a locally finite collection in $X \times Y$ . Define $V_{i,j}=\bigcup \mathcal{V}_{i,j}$ . The set $V_{i,j}$ is a union of closed sets. In general, the union of closed sets needs not be closed. However, $V_{i,j}$ is still a closed set in $X \times Y$ since $\mathcal{V}_{i,j}$ is a locally finite collection of closed sets. This is because a locally finite collection of sets is closure preserving. Note the following:

$\overline{V_{i,j}}=\overline{\bigcup \mathcal{V}_{i,j}}=\overline{\bigcup \left\{W_{B,j} \times \overline{B}: B \in \mathcal{B}_i^* \right\}}=\bigcup \left\{\overline{W_{B,j} \times \overline{B}}: B \in \mathcal{B}_i^* \right\}$

$=\bigcup \left\{W_{B,j} \times \overline{B}: B \in \mathcal{B}_i^* \right\}=V_{i,j}$

Finally, we have $U=\bigcup \limits_{i=1}^\infty \bigcup \limits_{j=1}^\infty V_{i,j}$ , which is the union of countably many closed sets. $\blacksquare$

Lemma 8
If $X$ is a paracompact space satisfying the following two conditions:

every open subset of $X$ is an $F_\sigma$ -set in $X$ ,
$Y$ is a metric space,

then $X \times Y$ is paracompact.

Proof of Lemma 8
As in the proof of the above lemma, let $\mathcal{B}=\bigcup \limits_{i=1}^\infty \mathcal{B}_i$ be a base for $Y$ such that each $\mathcal{B}_i$ is locally finite in $Y$ . Let $\mathcal{U}$ be an open cover of $X \times Y$ . Assume that elements of $\mathcal{U}$ are of the form $A \times B$ where $A$ is open in $X$ and $B \in \mathcal{B}$ .

For each $B \in \mathcal{B}$ , consider the following two items:

$\mathcal{W}_B=\left\{A: A \times B \in \mathcal{U} \right\}$

$W_B=\bigcup \mathcal{W}_B$

To simplify matter, we only consider $B \in \mathcal{B}$ such that $\mathcal{W}_B \ne \varnothing$ . Each $W_B$ is open in $X$ and hence by assumption an $F_\sigma$ -set in $X$ . Thus by Proposition 2, each $W_B$ is paracompact. Note that $\mathcal{W}_B$ is an open cover of $W_B$ . Let $\mathcal{H}_B$ be a locally finite open refinement of $\mathcal{W}_B$ . Consider the following two items:

$j=1,2,3,\cdots$

$\mathcal{V}_j=\left\{A \times B: A \in \mathcal{H}_B \text{ and } B \in \mathcal{B}_j \right\}$

$\mathcal{V}=\bigcup \limits_{j=1}^\infty \mathcal{V}_j$

We observe that $\mathcal{V}$ is an open cover of $X \times Y$ and that $\mathcal{V}$ refines $\mathcal{U}$ . Furthermore each $\mathcal{V}_j$ is a locally finite collection. The open cover $\mathcal{U}$ we start with has a $\sigma$ -locally finite open refinement. Thus $X \times Y$ is paracompact. $\blacksquare$

___________________________________________________________________________________

Result 4

Result 4 is the statement that:

$X$

$Y$

$X \times Y$

Proof of Result 4
Suppose $X$ is hereditarily Lindelof and that $Y$ is a separable metric space. It is well known that regular Lindelof spaces are paracompact. Thus $X$ is paracompact. By Proposition 5, $X$ is perfectly normal. By Result 3, $X \times Y$ is paracompact and perfectly normal.

Let $D$ be a countable dense subset of $Y$ . We can think of $D$ as a $\sigma$ -compact space. The product of any Lindelof space with a $\sigma$ -compact space is Lindelof (see Corollary 3 in the post “The Tube Lemma”). Thus $X \times D$ is Lindelof. Furthermore $X \times D$ is a dense Lindelof subspace of $X \times Y$ . By Proposition 3, $X \times Y$ is Lindelof. By Proposition 5, $X \times Y$ is hereditarily Lindelof. $\blacksquare$

Remark
In the previous post “Bernstein Sets and the Michael Line”, a non-normal product space where one factor is Lindelof and the other factor is a separable metric space is presented. That Lindelof space is not hereditarily Lindelof (it has uncountably many isolated points). Note that by Result 4, for any such non-normal product space, the Lindelof factor cannot be hereditarily Lindelof.

___________________________________________________________________________________

Reference

Engelking, R., General Topology, Revised and Completed edition, Heldermann Verlag, Berlin, 1989.
Willard, S., General Topology, Addison-Wesley Publishing Company, 1970.

___________________________________________________________________________________

$\copyright \ \ 2012$

Cartesian Products of Two Paracompact Spaces

Posted on November 8, 2012 by Dan Ma

In some previous posts we discuss examples surrounding the Michael line showing that the product of a paracompact space and a complete metric space needs not be normal (see “Michael Line Basics”) and that the product of a Lindelof space and a separable metric space need not be normal (see “Bernstein Sets and the Michael Line”). These examples are classic counterexamples demonstrating that both paracompactness and Lindelofness are not preserved by taking two-factor cartesian products even when one of the factors is nice (complete metric space in the first example and separable metric space in the second example). We now show some positive results. Of course, these results require additional conditions on one or both of the factors. We prove the following results.

Result 1

$X$

$Y$

$X \times Y$

Result 2

$X$

$Y$

$\sigma$

$X \times Y$

Result 3

$X$

$Y$

$X \times Y$

Result 4

$X$

$Y$

$X \times Y$

With Results 1 and 2, compact spaces and $\sigma$ -compact spaces can be called productively paracompact since the product of each of these spaces with any paracompact space is paracompact. We prove Result 1 and Result 2 below.

Result 3 and Result 4 are proved in another post Cartesian Products of Two Paracompact Spaces – Continued.

___________________________________________________________________________________

Paracompact Spaces

First, recall some definitions. All spaces are at least regular (to us regular implies Hausdorff). Let $X$ be a space. A collection $\mathcal{A}$ of subsets of $X$ is said to be a cover of $X$ if $X=\bigcup \mathcal{A}$ (in words every point of the space belongs to one set in the collection). Furthermore, $\mathcal{A}$ is an open cover of $X$ is it is a cover of $X$ consisting of open subsets of $X$ .

Let $\mathcal{A}$ and $\mathcal{B}$ be covers of the space $X$ . The cover $\mathcal{B}$ is said to be a refinement of $\mathcal{A}$ ( $\mathcal{B}$ is said to refine $\mathcal{A}$ ) if for every $B \in \mathcal{B}$ , there is some $A \in \mathcal{A}$ such that $B \subset A$ . The cover $\mathcal{B}$ is said to be an open refinement of $\mathcal{A}$ if $\mathcal{B}$ refines $\mathcal{A}$ and $\mathcal{B}$ is an open cover.

A collection $\mathcal{A}$ of subsets of $X$ is said to be a locally finite collection if for each point $x \in X$ , there is a non-empty open subset $V$ of $X$ such that $x \in V$ and $V$ has non-empty intersection with at most finitely many sets in $\mathcal{A}$ . An open cover $\mathcal{A}$ of $X$ is said to have a locally finite open refinement if there exists an open cover $\mathcal{C}$ of $X$ such that $\mathcal{C}$ refines $\mathcal{A}$ and $\mathcal{C}$ is a locally finite collection. We have the following definition.

Definition

$X$

A collection $\mathcal{U}$ of subsets of the space $X$ is said to be a $\sigma$ -locally finite collection if $\mathcal{U}=\bigcup \limits_{i=1}^\infty \mathcal{U}_i$ such that each $\mathcal{U}_i$ is a locally finite collection of subsets of $X$ . Consider the property that every open cover of $X$ has a $\sigma$ -locally finite open refinement. This on the surface is a stronger property than paracompactness. However, Theorem 1 below shows that it is actually equivalent to paracompactness. The proof of Theorem 1 can be found in [1] (Theorem 5.1.11 in page 302) or in [2] (Theorem 20.7 in page 146).

Theorem 1
Let $X$ be a regular space. Then $X$ is paracompact if and only if every open cover $\mathcal{U}$ of $X$ has a $\sigma$ -locally finite open refinement.

Theorem 2 below is another characterization of paracompactness that is useful. For a proof of Theorem 2, see “Finite and Countable Products of the Michael Line”.

Theorem 2
Let $X$ be a regular space. Then $X$ is paracompact if and only if the following holds:

$\left\{U_t: t \in T \right\}$

$X$

$\left\{V_t: t \in T \right\}$

$\overline{V_t} \subset U_t$

$t \in T$

Theorem 3 below shows that paracompactness is hereditary with respect to $F_\sigma$ -subsets.

Theorem 3
Every $F_\sigma$ -subset of a paracompact space is paracompact.

Proof of Theorem 3
Let $X$ be paracompact. Let $Y \subset X$ such that $Y=\bigcup \limits_{i=1}^\infty Y_i$ where each $Y_i$ is a closed subset of $X$ . Let $\mathcal{U}$ be an open cover of $Y$ . For each $U \in \mathcal{U}$ , let $U^*$ be open in $X$ such that $U^* \cap Y=U$ .

For each $i$ , let $\mathcal{U}_i^*$ be the set of all $U^*$ such that $U \cap Y_i \ne \varnothing$ . Let $\mathcal{V}_i^*$ be a locally finite refinement of $\mathcal{U}_i^* \cup \left\{X-Y_i \right\}$ . Let $\mathcal{V}_i$ be the following:

$\mathcal{V}_i=\left\{V \cap Y: V \in \mathcal{V}_i^* \text{ and } V \cap Y_i \ne \varnothing \right\}$

It is clear that each $\mathcal{V}_i$ is a locally finite collection of open set in $Y$ covering $Y_i$ . All the $\mathcal{V}_i$ together form a refinement of $\mathcal{U}$ . Thus $\mathcal{V}=\bigcup \limits_{i=1}^\infty \mathcal{V}_i$ is a $\sigma$ -locally finite open refinement of $\mathcal{U}$ . By Theorem 1, the $F_\sigma$ -set $Y$ is paracompact. $\blacksquare$
___________________________________________________________________________________

Result 1

Result 1 is the statement that:

$X$

$Y$

$X \times Y$

To prove Result 1, we use the Tube lemma (for a proof, see “The Tube Lemma”).

The Tube Lemma
Let $X$ be any space and $Y$ be compact. For each $x \in X$ and for each open set $U \subset X \times Y$ such that $\left\{x \right\} \times Y \subset U$ , there is an open set $O \subset X$ such that $\left\{x \right\} \times Y \subset O \times Y \subset U$ .

Proof of Result 1
Let $\mathcal{U}$ be an open cover of $X \times Y$ . For each $x \in X$ , choose a finite $\mathcal{U}_x \subset \mathcal{U}$ such that $\mathcal{U}_x$ is a cover of $\left\{x \right\} \times Y$ . By the Tube Lemma, for each $x \in X$ , there is an open set $O_x \subset X$ such that $\left\{x \right\} \times Y \subset O_x \times Y \subset \cup \mathcal{U}_x$ . Since $X$ is paracompact, by Theorem 2, let $\left\{W_x: x \in X \right\}$ be a locally finite open refinement of $\left\{O_x: x \in X \right\}$ such that $W_x \subset O_x$ for each $x \in X$ .

Let $\mathcal{W}=\left\{(W_x \times Y) \cap U: x \in X, U \in \mathcal{U}_x \right\}$ . We claim that $\mathcal{W}$ is a locally finite open refinement of $\mathcal{U}$ . First, this is an open cover of $X \times Y$ . To see this, let $(a,b) \in X \times Y$ . Then $a \in W_x$ for some $x \in X$ . Furthermore, $a \in O_x$ and $(a,b) \in \cup \mathcal{U}_x$ . Thus, $(a,b) \in (W_x \times Y) \cap U$ for some $U \in \mathcal{U}_x$ . Secondly, it is clear that $\mathcal{W}$ is a refinement of the original cover $\mathcal{U}$ .

It remains to show that $\mathcal{W}$ is locally finite. To see this, let $(a,b) \in X \times Y$ . Then there is an open $V$ in $X$ such that $x \in V$ and $V$ can meets only finitely many $W_x$ . Then $V \times Y$ can meet only finitely many sets in $\mathcal{W}$ . $\blacksquare$

___________________________________________________________________________________

Result 2

Result 2 is the statement that:

$X$

$Y$

$\sigma$

$X \times Y$

Proof of Result 2
Note that the $\sigma$ -compact space $Y$ is Lindelof. Since regular Lindelof are normal, $Y$ is normal and is thus completely regular. So we can embed $Y$ into a compact space $K$ . For example, we can let $K=\beta Y$ , which is the Stone-Cech compactification of $Y$ (see “Embedding Completely Regular Spaces into a Cube”). For our purpose here, any compact space containing $Y$ will do. By Result 1, $X \times K$ is paracompact. Note that $X \times Y$ can be regarded as a subspace of $X \times K$ .

Let $Y=\bigcup \limits_{i=1}^\infty Y_i$ where each $Y_i$ is compact in $Y$ . Note that $X \times Y=\bigcup \limits_{i=1}^\infty X \times Y_i$ and each $X \times Y_i$ is a closed subset of $X \times K$ . Thus the product $X \times Y$ is an $F_\sigma$ -subset of $X \times K$ . According to Theorem 3, $F_\sigma$ -subsets of any paracompact space is paracompact space. Thus $X \times Y$ is paracompact. $\blacksquare$

___________________________________________________________________________________

Reference

Engelking, R., General Topology, Revised and Completed edition, Heldermann Verlag, Berlin, 1989.
Willard, S., General Topology, Addison-Wesley Publishing Company, 1970.

___________________________________________________________________________________

$\copyright \ \ 2012$

Alexandroff Double Circle

Posted on October 13, 2012 by Dan Ma

We discuss the Alexandroff double circle, which is a compact and non-metrizable space. A theorem about the hereditarily normality of a product space $Y_1 \times Y_2$ is also discussed.

Let $C_1$ and $C_2$ be the two concentric circles centered at the origin with radii 1 and 2, respectively. Specifically $C_i=\left\{(x,y) \in \mathbb{R}^2: x^2 + y^2 =i \right\}$ where $i=1,2$ . Let $X=C_1 \cup C_2$ . Furthermore let $f:C_1 \rightarrow C_2$ be the natural homeomorphism. Figure 1 below shows the underlying set.

_______________________________________________________________
Figure 1 – Underlying Set

_______________________________________________________________

We define a topology on $X$ as follows:

Points in $C_2$ are isolated.
For each and for each positive integer , let be the open arc in whose center contains and has length (in the Euclidean topology on ). For each , an open neighborhood is of the form where
The following figure shows an open neighborhood at point in $C_1$ .

_______________________________________________________________
Figure 2 – Open Neighborhood

___________________________________________________________________________________

A List of Results

It can be verified that the open neighborhoods defined above form a base for a topology on $X$ . We discuss the following points about the Alexandroff double circle.

$X$ is a Hausdorff space.
$X$ is not separable.
$X$ is not hereditarily Lindelof.
$X$ is compact.
$X$ is sequentially compact.
$X$ is not metrizable.
$X$ is not perfectly normal.
$X$ is completely normal (and thus hereditarily normal).
$X \times X$ is not hereditarily normal.

The proof that $X \times X$ is not hereditarily normal can be generalized. We discuss this theorem after presenting the proof of Result 9.
___________________________________________________________________________________

Results 1, 2, 3

It is clear that the Alexandroff double circle is a Hausdorff space. It is not separable since the outer circle $C_2$ consists of uncountably many singleton open subsets. For the same reason, $C_2$ is a non-Lindelof subspace, making the Alexandroff double circle not hereditarily Lindelof. $\blacksquare$

___________________________________________________________________________________

Result 4

The property that $X$ is compact is closely tied to the compactness of the inner circle $C_1$ in the Euclidean topology. Note that the subspace topology of the Alexandroff double circle on $C_1$ is simply the Euclidean topology. Let $\mathcal{U}$ be an open cover of $X$ consisting of open sets as defined above. Then there are finitely many basic open sets $B(x_1,j_1)$ , $B(x_2,j_2)$ , $\cdots$ , $B(x_n,j_n)$ from $\mathcal{U}$ covering $C_1$ . These open sets cover the entire space except for the points $f(x_1), f(x_2), \cdots,f(x_n)$ , which can be covered by finitely many open sets in $\mathcal{U}$ . $\blacksquare$

___________________________________________________________________________________

Result 5

A space $W$ is sequentially compact if every sequence of points of $W$ has a subsequence that converges to a point in $W$ . The notion of sequentially compactness and compactness coincide for the class of metric spaces. However, in general these two notions are distinct.

The sequentially compactness of the Alexandroff double circle $X$ hinges on the sequentially compactness of $C_1$ and $C_2$ in the Euclidean topology. Let $\left\{x_n \right\}$ be a sequence of points in $X$ . If the set $\left\{x_n: n=1,2,3,\cdots \right\}$ is a finite set, then $\left\{x_n: n>m \right\}$ is a constant sequence for some large enough integer $m$ . So assume that $A=\left\{x_n: n=1,2,3,\cdots \right\}$ is an infinite set. Either $A \cap C_1$ is infinite or $A \cap C_2$ is infinite. If $A \cap C_1$ is infinite, then some subsequence of $\left\{x_n \right\}$ converges in $C_1$ in the Euclidean topology (hence in the Alexandroff double circle topology). If $A \cap C_2$ is infinite, then some subsequence of $\left\{x_n \right\}$ converges to $x \in C_2$ in the Euclidean topology. Then this same subsequence converges to $f^{-1}(x)$ in the Alexandroff double circle topology. $\blacksquare$

___________________________________________________________________________________

Result 6

Note that any compact metrizable space satisfies a long list of properties, which include separable, Lindelof, hereditarily Lindelof. $\blacksquare$

___________________________________________________________________________________

Result 7

A space is perfectly normal if it is normal with the additional property that every closed set is a $G_\delta$ -set. For the Alexandroff double circle, the inner circle $C_1$ is not a $G_\delta$ -set, or equivalently the outer circle $C_2$ is not an $F_\sigma$ -set. To see this, suppose that $C_2$ is the union of countably many sets, we show that the closure of at least one of the sets goes across to the inner circle $C_1$ . Let $C_2=\bigcup \limits_{i=1}^\infty T_n$ . At least one of the sets is uncountable. Let $T_j$ be one such. Consider $f^{-1}(T_j)$ , which is also uncountable and has a limit point in $C_1$ (in the Euclidean topology). Let $t$ be one such point (i.e. every Euclidean open set containing $t$ contains points of $f^{-1}(T_j)$ ). Then the point $t$ is a member of the closure of $T_j$ (Alexandroff double circle topology). $\blacksquare$

___________________________________________________________________________________

Result 8

We first discuss the notion of separated sets. Let $T$ be a Hausdorff space. Let $E \subset T$ and $F \subset T$ . The sets $E$ and $F$ are said to be separated (are separated sets) if $E \cap \overline{F}=\varnothing$ and $F \cap \overline{E}=\varnothing$ . In other words, two sets are separated if each one does not meet the closure of the other set. In particular, any two disjoint closed sets are separated. The space $T$ is said to be completely normal if $T$ satisfies the property that for any two sets $E$ and $F$ that are separated, there are disjoint open sets $U$ and $V$ with $E \subset U$ and $F \subset V$ . Thus completely normality implies normality.

It is a well know fact that if a space is completely normal, it is hereditarily normal (actually the two notions are equivalent). Note that any metric space is completely normal. In particular, any Euclidean space is completely normal.

To show that the Alexandroff double circle $X$ is completely normal, let $E \subset X$ and $F \subset X$ be separated sets. Thus we have $E \cap \overline{F}=\varnothing$ and $F \cap \overline{E}=\varnothing$ . Note that $E \cap C_1$ and $F \cap C_1$ are separated sets in the Euclidean space $C_1$ . Let $G_1$ and $G_2$ be disjoint Euclidean open subsets of $C_1$ with $E \cap C_1 \subset G_1$ and $F \cap C_1 \subset G_2$ .

For each $x \in E \cap C_1$ , choose open $U_x$ (Alexandroff double circle open) with $x \in U_x$ , $U_x \cap C_1 \subset G_1$ and $U_x \cap \overline{F}=\varnothing$ . Likewise, for each $y \in F \cap C_1$ , choose open $V_y$ (Alexandroff double circle open) with $y \in V_y$ , $V_y \cap C_1 \subset G_2$ and $V_y \cap \overline{E}=\varnothing$ . Then let $U$ and $V$ be defined by the following:

$U=\biggl(\bigcup \limits_{x \in E \cap C_1} U_x \biggr) \cup \biggl(E \cap C_2 \biggr)$

$\text{ }$

$V= \biggl(\bigcup \limits_{y \in F \cap C_1} V_y \biggr) \cup \biggl(F \cap C_2 \biggr)$

Because $G_1 \cap G_2 =\varnothing$ , the open sets $U_x$ and $V_y$ are disjoint. As a result, $U$ and $V$ are disjoint open sets in the Alexandroff double circle with $E \subset U$ and $F \subset V$ .

For the sake of completeness, we show that any completely normal space is hereditarily normal. Let $T$ be completely normal. Let $Y \subset T$ . Let $H \subset Y$ and $K \subset Y$ be disjoint closed subsets of $Y$ . Then in the space $T$ , $H$ and $K$ are separated. Note that $H \cap cl_T(K)=\varnothing$ and $K \cap cl_T(H)=\varnothing$ (where $cl_T$ gives the closure in $T$ ). Then there are disjoint open subsets $O_1$ and $O_2$ of $T$ such that $H \subset O_1$ and $K \subset O_2$ . Now, $O_1 \cap Y$ and $O_2 \cap Y$ are disjoint open sets in $Y$ such that $H \subset O_1 \cap Y$ and $K \subset O_2 \cap Y$ .

Thus we have established that the Alexandroff double circle is hereditarily normal. $\blacksquare$

For the proof that a space is completely normal if and only if it is hereditarily normal, see Theorem 2.1.7 in page 69 of [1],
___________________________________________________________________________________

Result 9

We produce a subspace $Y \subset X \times X$ that is not normal. To this end, let $D=\left\{d_n:n=1,2,3,\cdots \right\}$ be a countable subset of $X$ such that $\overline{D}-D\ne \varnothing$ . Let $y \in \overline{D}-D$ . Let $Y=X \times X-C_1 \times \left\{y \right\}$ . We show that $Y$ is not normal.

Let $H=C_1 \times (X-\left\{y \right\})$ and $K=C_2 \times \left\{y \right\}$ . These are two disjoint closed sets in $Y$ . Let $U$ and $V$ be open in $Y$ such that $H \subset U$ and $K \subset V$ . We show that $U \cap V \ne \varnothing$ .

For each integer $j$ , let $U_j=\left\{x \in X: (x,d_j) \in U \right\}$ . We claim that each $U_j$ is open in $X$ . To see this, pick $x \in U_j$ . We know $(x,d_j) \in U$ . There exist open $A$ and $B$ (open in $X$ ) such that $(x,d_j) \in A \times B \subset U$ . It is clear that $x \in A \subset U_j$ . Thus each $U_j$ is open.

Furthermore, we have $C_1 \subset U_j$ for each $j$ . Based in Result 7, $C_1$ is not a $G_\delta$ -set. So we have $C_1 \subset \bigcap \limits_{j=1}^\infty U_j$ but $C_1 \ne \bigcap \limits_{j=1}^\infty U_j$ . There exists $t \in \bigcap \limits_{j=1}^\infty U_j$ but $t \notin C_1$ . Thus $t \in C_2$ and $\left\{t \right\}$ is open.

Since $(t,y) \in K$ , we have $(t,y) \in V$ . Choose an open neighborhood $B(y,k)$ of $y$ such that $\left\{t \right\} \times B(y,k) \subset V$ . since $y \in \overline{D}$ , there exists some $d_j$ such that $(t,d_j) \in \left\{t \right\} \times B(y,k)$ . Hence $(t,d_j) \in V$ . Since $t \in U_j$ , $(t,d_j) \in U$ . Thus $U \cap V \ne \varnothing$ . $\blacksquare$

___________________________________________________________________________________

Generalizing the Proof of Result 9

The proof of Result 9 requires that one of the factors has a countable set that is not discrete and the other factor has a closed set that is not a $G_\delta$ -set. Once these two requirements are in place, we can walk through the same proof and show that the cross product is not hereditarily normal. Thus, the statement that is proved in Result 9 is the following.

Theorem
If $Y_1$ has a countable subset that is not closed and discrete and if $Y_2$ has a closed set that is not a $G_\delta$ -set then $Y_1 \times Y_2$ has a subspace that is not normal.

The theorem can be restated as:

Theorem
If $Y_1 \times Y_2$ is hereditarily normal, then either every countable subset of $Y_1$ is closed and discrete or $Y_2$ is perfectly normal.

The above theorem is due to Katetov and can be found in [2]. It shows that the hereditarily normality of a cross product imposes quite strong restrictions on the factors. As a quick example, if both $Y_1$ and $Y_2$ are compact, for $Y_1 \times Y_2$ to be hereditarily normal, both $Y_1$ and $Y_2$ must be perfectly normal.

Another example. Let $W=\omega_1+1$ , the succesor of the first uncountable ordinal with the order topology. Note that $W$ is not perfectly normal since the point $\omega_1$ is not a $G_\delta$ point. Then for any compact space $Y$ , $W \times Y$ is not hereditarily normal. Let $C=\omega+1$ , the successor of the first infinite ordinal with the order topology (essentially a convergent sequence with the limit point). The product $W \times C$ is the Tychonoff plank and based on the discussion here is not hereditarily normal. Usually the Tychonoff plank is shown to be not hereditarily normal by removing the cornor point $(\omega_1,\omega)$ . The resulting space is the deleted Tychonoff plank and is not normal (see The Tychonoff Plank).

___________________________________________________________________________________

Reference

Engelking, R., General Topology, Revised and Completed edition, Heldermann Verlag, Berlin, 1989.
Przymusinski, T. C., Handbook of Set-Theoretic Topology (K. Kunen and J. E. Vaughan, eds), Elsevier Science Publishers B. V., Amsterdam, 781-826, 1984.
Willard, S., General Topology, Addison-Wesley Publishing Company, 1970.

___________________________________________________________________________________

Sorgenfrey Line is not a Moore Space

Posted on September 18, 2012 by Dan Ma

We found an incorrect statement about the Sorgenfrey line in an entry in Wikipedia about Moore space (link). This statement opens up a discussion on the question of whether the Sorgenfrey line is a Moore space as well as a discussion on Moore space. The following is the incorrect statement found in Wikipedia by the author.

5. Neither the Sorgenfrey line nor the Sorgenfrey plane are Moore spaces because they are normal and not second countable

The Sorgenfrey line is the space whose underlying set is the real line $S=\mathbb{R}$ where the topology is generated by a base consisting the half open intervals of the form $[a,b)$ . The Sorgenfrey plane is the square $S \times S$ .

Even though the Sorgenfrey line is normal, the Sorgenfrey plane is not normal. In fact, the Sorgenfrey line is the classic example of a normal space whose square is not normal. Both the Sorgenfrey line and the Sorgenfrey plane are not Moore space but not for the reason given. The statement seems to suggest that any normal Moore space is second countable. But this flies in the face of all the profound mathematics surrounding the normal Moore space conjecture, which is also discussed in the Wikipedia entry.

The statement indicated above is only a lead-in to a discussion of Moore space. We are certain that it will be corrected. We always appreciate readers who kindly alert us to errors found in this blog.

______________________________________________________________________________

Moore Spaces

Let $X$ be a regular space. A development for $X$ is a sequence $\mathcal{G}_1,\mathcal{G}_2,\mathcal{G}_3,\cdots$ of open covers of $X$ such that for each $x \in X$ , and for each open subset $U$ of $X$ with $x \in U$ , there exists one cover $\mathcal{G}_n$ satisfying the condition that for any open set $V \in \mathcal{G}_n$ , $x \in V \Rightarrow V \subset U$ . When $X$ has a development, $X$ is said to be a Moore space (also called developable space). A Note On The Sorgenfrey Line is an introductory note on the Sorgenfrey line.

Moore spaces can be viewed as a generalization of metrizable spaces. Moore spaces are first countable (having a countable base at each point). For a development $\mathcal{G}_1,\mathcal{G}_2,\mathcal{G}_3,\cdots$ , the open sets in $\mathcal{G}_n$ are considered “smaller” as the index $n$ increases. In fact, this is how a development is defined for a metric space, where $\mathcal{G}_n$ consists of all open balls with diameters less than $\frac{1}{n}$ . Thus metric spaces are developable. There are plenty of non-metrizable Moore space. One example is the Niemytzki’s Tangent Disc space.

In a Moore space, every closed set is a $G_\delta$ -set. Thus if a Moore space is normal, it is perfectly normal. Any Moore space has a $G_\delta$ -diagonal (the diagonal $\Delta=\left\{(x,x): x \in X \right\}$ is a $G_\delta$ -set in $X \times X$ ). It is a well known theorem that every compact space with a $G_\delta$ -diagonal is metrizable. Thus any compact Moore space is metrizable.

The last statement can be shown more directly. Suppose that $X$ is compact and has a development $\mathcal{G}_1,\mathcal{G}_2,\mathcal{G}_3,\cdots$ . Then each $\mathcal{G}_n$ has a finite subcover $\mathcal{H}_n$ . Then $\bigcup_{n=1}^\infty \mathcal{H}_n$ is a countable base for $X$ . Thus any compact Moore space is second countable and hence metrizable.

What about paracompact Moore space? Suppose that $X$ is paracompact and has a development $\mathcal{G}_1,\mathcal{G}_2,\mathcal{G}_3,\cdots$ . Then each $\mathcal{G}_n$ has a locally finite open refinement $\mathcal{H}_n$ . Then $\bigcup_{n=1}^\infty \mathcal{H}_n$ is a $\sigma$ -locally finite base for $X$ . The Smirnov-Nagata metrization theorem states that a space is metrizable if and only if it has a $\sigma$ -locally finite base (see Theorem 23.9 on page 170 of [2]). Thus any paracompact Moore space has a $\sigma$ -locally finite base and is thus metrizable (after using the big gun of the Smirnov-Nagata metrization theorem).

______________________________________________________________________________

Sorgenfrey Line

The Sorgenfrey line is regular and Lindelof. Hence it is paracompact. Since the Sorgenfrey line is not metrizable, by the above discussion it cannot be a Moore space. The Sorgenfrey plane is also not a Moore space. Note that being a Moore space is a hereditary property. So if the Sorgenfrey plane is a Moore space, then every subspace of the Sorgenfrey plane (including the Sorgenfrey line) is a Moore space.

The following theorem is another way to show that the Sorgenfrey line is not a Moore space.

Bing’s Metrization Theorem

Every paracompact space is collectionwise normal (see Theorem 5.1.18, p.305 of [1]). Thus the Sorgenfrey line is collectionwise normal and hence cannot be a Moore space. A space $X$ is said to be collectionwise normal if $X$ is a $T_1$ -space and for every discrete collection $\left\{W_\alpha: \alpha \in A \right\}$ of closed sets in $X$ , there exists a discrete collection $\left\{V_\alpha: \alpha \in A \right\}$ of open subsets of $X$ such that $W_\alpha \subset V_\alpha$ . For a proof of Bing’s metrization theorem, see page 329 of [1].

______________________________________________________________________________

Remark

The normal Moore space conjecture is the statement that every normal Moore space is metrizable. This conjecture had been one of the key motivating questions for many set theorists and topologists during a large part of the twentieth century. The bottom line is that this statement cannot not be decided just on the basis of the set of generally accepted axioms called Zermelo–Fraenkel set theory with the axiom of choice, commonly abbreviated ZFC. But Bing’s metrization theorem states that if we strengthen normality to collectionwise normality, we have a definite answer.

______________________________________________________________________________

Reference

Engelking, R., General Topology, Revised and Completed edition, Heldermann Verlag, Berlin, 1989.
Willard, S., General Topology, Addison-Wesley Publishing Company, 1970.

______________________________________________________________________________

One way to get CCC spaces that are not separable

Posted on September 14, 2012 by Dan Ma

A space $X$ is said to have countable chain condition (ccc) if every disjoint collection of open subsets of $X$ is countable. For convenience, we refer to spaces that have countable chain condition as ccc spaces. It is easy to verify that separable spaces are ccc spaces. We present a specific way of generating spaces that always have ccc but are not separable. These spaces are the sigma products of separable spaces.

The product of separable spaces always have ccc (see Product of Spaces with Countable Chain Condition). However, the product of separable spaces is not separable when the number of factors is greater than continuum. Thus one way to get an example of ccc but not separable space is to take the product of more than continuum many separable spaces. For example, if $c$ is the cardinality of continuum, $\left\{0,1 \right\}^{2^c}$ , the product of $2^c$ many copies of $\left\{0,1 \right\}$ , is a space that has ccc but is not separable.

________________________________________________________________________

Another example is obtained from taking sigma product of separable spaces. Let $\left\{X_\alpha: \alpha \in A \right\}$ be a collection of spaces where $A$ is some index set. Consider the product space $\prod \limits_{\alpha \in A} X_\alpha$ . Fix a point $p$ in the product. The sigma-product about the point $p$ is denoted by $\sum \limits_{\alpha \in A} X_\alpha$ and is the following subspace of the product space $\prod \limits_{\alpha \in A} X_\alpha$ :

$\sum \limits_{\alpha \in A} X_\alpha=\left\{x \in \prod \limits_{\alpha \in A} X_\alpha: x(\alpha) \ne p(\alpha) \text{ for at most countably many } \alpha \right\}$

To obtain the desired example, let $A$ be an uncountable index set and let each $X_\alpha$ be separable. The product space $\prod \limits_{\alpha \in A} X_\alpha$ has ccc. Note that $\sum \limits_{\alpha \in A} X_\alpha$ is always dense in the product space $\prod \limits_{\alpha \in A} X_\alpha$ . Thus the sigma-product $\sum \limits_{\alpha \in A} X_\alpha$ has ccc since it is a dense subspace of a ccc space. On the other hand, $\sum \limits_{\alpha \in A} X_\alpha$ is never separable as long as there are uncountably many spaces $X_\alpha$ .

As specific example, take $X_\alpha=\left\{0,1 \right\}$ for each $\alpha < \omega_1$ and let the fixed point $p$ be such that $p(\alpha)=0$ for all $\alpha < \omega_1$ . The resulting $\sum \limits_{\alpha < \omega_1} \left\{0,1 \right\}$ is a ccc space that is not separable. Of course, $\sum \limits_{\alpha < \omega_1} X_\alpha$ in this case is the set of all $x \in \left\{0,1 \right\}^{\omega_1}$ such that $x(\alpha) \ne 0$ for at most countably many $\alpha < \omega_1$ .

One interesting note about the sigma-product $\sum \limits_{\alpha < \omega_1} \left\{0,1 \right\}$ is that the overall product space $\left\{0,1 \right\}^{\omega_1}$ is an example of a separable but not hereditarily separable space. Another interesting point is that $\sum \limits_{\alpha < \omega_1} \left\{0,1 \right\}$ is a countably compact non-compact space (see A note about sigma-product of compact spaces).

________________________________________________________________________

Previous discussion of CCC spaces in this blog:

Product of Spaces with Countable Chain Condition

Some basic properties spaces with countable chain condition

________________________________________________________________________

Reference

Engelking, R., General Topology, Revised and Completed edition, Heldermann Verlag, Berlin, 1989.
Willard, S., General Topology, Addison-Wesley Publishing Company, 1970.

________________________________________________________________________

Some basic properties of spaces with countable chain condition

Posted on September 8, 2012 by Dan Ma

A space $X$ is said to have countable chain condition (ccc) if every disjoint collection of open subsets of $X$ is countable. When a space has ccc, for convenience we also say that it is a ccc space. We present some basic results about ccc space as well as an equivalent condition for ccc in terms of relatively locally finite open collection. A corollary of this equivalent condition is that in the class of ccc spaces, paracompactness coincides with the Lindelof property.

____________________________________________________________________________

Basic Properties

Let $X$ be a space. We have the following simple results about ccc spaces.

If $X$ is separable, then $X$ has ccc.
If $X$ is hereditarily Lindelof, then $X$ has ccc.
The property ccc is hereditary with respect to open subspaces.
Let $Y$ be a dense subspace of $X$ . Then $Y$ has ccc if and only if $X$ has ccc.

We only prove result 4.

Proof of 4
Let $Y$ be a dense subspace of the space $X$ . Suppose that $X$ does not have ccc. Then there is an uncountable disjoint collection $\mathcal{U}$ of open subsets of $X$ . Assuming that $Y$ is an uncountable set, the collection of all $U \cap Y$ (where $U \in \mathcal{U}$ ) is an uncountable disjoint collection of open subsets of $Y$ . It follows that $Y$ does not have ccc. Thus $Y$ has ccc implies $X$ has ccc.

Suppose that $Y$ does not have ccc. Then there is an uncountable disjoint collection $\mathcal{V}$ of open subsets of $Y$ . For each $V \in \mathcal{V}$ , there is some $V^*$ , open subset of $X$ , such that $V=V^* \cap Y$ . Let $\mathcal{V}^*$ be the collection of all $V^*$ . Note that $\mathcal{V}^*$ is uncountable and is a disjoint collection of open subsets of $X$ . It follows that $X$ does not have ccc. Thus $X$ has ccc implies $Y$ has ccc. $\blacksquare$

Theorem 1 and Corollary 2 (stated below) are discussed in a previous post (Product of Spaces with Countable Chain Condition). Theorem 1 implies that if the ccc property is preserved by taking product of any finite number of factors, then the ccc property is preserved by taking product of any number of factors. As a corollary, it follows that the product of any number of separable spaces has ccc.

Theorem 1
Suppose that $\left\{X_\alpha: \alpha \in T \right\}$ is a family of spaces such that $\prod \limits_{\alpha \in F} X_\alpha$ has countable chain condition for every finite $F \subset T$ . Then $\prod \limits_{\alpha \in T} X_\alpha$ has countable chain condition.

Corollary 2
Suppose that $\left\{X_\alpha: \alpha \in T \right\}$ is a family of separable spaces. Then $\prod \limits_{\alpha \in T} X_\alpha$ has countable chain condition.

____________________________________________________________________________

An Equivalent Condition for Countable Chain Condition

The next theorem is an alternative way of looking at countable chain condition. Corollary 3 is an application of this equivalent condition.

Theorem 3
Let $X$ be a space. Then the following conditions are equivalent.

If $\mathcal{U}$ is a collection of open subsets of $X$ such that $\mathcal{U}$ is locally countable in the open subspace $\bigcup \mathcal{U}$ , then $\mathcal{U}$ is countable.
If $\mathcal{U}$ is a collection of open subsets of $X$ such that $\mathcal{U}$ is locally finite in the open subspace $\bigcup \mathcal{U}$ , then $\mathcal{U}$ is countable.
$X$ has ccc.

Note that when an open collection $\mathcal{U}$ is locally finite (locally countable) in the open subspace $\bigcup \mathcal{U}$ , $\mathcal{U}$ is said to be a relatively locally finite (locally countable) open collection.

Proof
The directions $1 \Rightarrow 2$ and $2 \Rightarrow 3$ are clear.

$3 \Rightarrow 1$
Suppose that $X$ has ccc. Let $\mathcal{U}$ be a collection of open subsets of $X$ such that $\mathcal{U}$ is locally countable in the open subspace $\bigcup \mathcal{U}$ . For each $U \in \mathcal{U}$ , choose a non-empty open set $f(U) \subset U$ such that $f(U) \cap O \ne \varnothing$ for at most countably many $O \in \mathcal{U}$ . Let $\mathcal{U}_f$ be the collection of all $f(U)$ (over all $U \in \mathcal{U}$ ). Note that $f$ is a countable-to-one mapping from $\mathcal{U}$ into $\mathcal{U}_f$ .

For $H,K \in \mathcal{U}_f$ , a chain from $H$ to $K$ is any finite collection

$\left\{A_1,A_2,\cdots,A_n \right\} \subset \mathcal{U}_f$

such that $H=A_1$ , $K=A_n$ , and for $1 \le j < n$ , $A_j \cap A_{j+1} \ne \varnothing$ . For each $V \in \mathcal{U}_f$ , let $\mathcal{C}(V)$ be the following:

$\mathcal{C}(V)=\left\{W \in \mathcal{U}_f: \text{ there exists a chain from } V \text{ to } W \right\}$

Note that every $V \in \mathcal{U}_f$ meets only countably many sets in $\mathcal{U}$ . Thus every $V \in \mathcal{U}_f$ meets only countably many sets in $\mathcal{U}_f$ . As a result, each $\mathcal{C}(V)$ is countable. For each $V \in \mathcal{U}_f$ , let $\mathcal{E}(V)=\bigcup \mathcal{C}(V)$ . For $V_1,V_2 \in \mathcal{U}_f$ , if $\mathcal{E}(V_1) \cap \mathcal{E}(V_2) \ne \varnothing$ , $\mathcal{C}(V_1)=\mathcal{C}(V_2)$ , and as a result $\mathcal{E}(V_1)=\mathcal{E}(V_2)$ . Thus the collection of all distinct $\mathcal{E}(V)$ is a collection of disjoint open sets in $X$ . Since $X$ has ccc, there can be only countably many $\mathcal{E}(V)$ .

Each $\mathcal{E}(V)$ is the union of countably many open sets, namely the open sets in $\mathcal{C}(V)$ , which is countable. Each set $f(U) \in \mathcal{C}(V)$ is traced back to at most countably many sets in open sets $U$ in the original collection $\mathcal{U}$ . Since the mapping $f$ is a countable-to-one map from $\mathcal{U}$ to $\mathcal{U}_f$ , $\mathcal{U}$ is countable. $\blacksquare$

Corollary 4
Let $X$ be a space with countable chain condition. Then $X$ is a paracompact space if and only if $X$ is a Lindelof space.

Proof
The direction $\Leftarrow$ is the theorem that every regular Lindelof space is paracompact. See Theorem 3.8.11 and Theorem 5.1.2 in [1]. Also see Corollary 20.8 in [2].

$\Rightarrow$
This direction is a corollary of Theorem 3. Since $X$ is paracompact, every open cover of the space $X$ has a locally finite open refinement. By Theorem 3, the locally finite open refinement must be countable. $\blacksquare$

____________________________________________________________________________

Reference

Engelking, R., General Topology, Revised and Completed edition, Heldermann Verlag, Berlin, 1989.
Willard, S., General Topology, Addison-Wesley Publishing Company, 1970.

____________________________________________________________________________

Dan Ma's Topology Blog

Expository Articles In General Topology

Tag Archives: Hereditarily lindelof

A little corner in the world of set-theoretic topology

Equivalent conditions for hereditarily Lindelof spaces

Cp(X) where X is a separable metric space

Pixley-Roy hyperspaces

Cartesian Products of Two Paracompact Spaces – Continued

Cartesian Products of Two Paracompact Spaces

Alexandroff Double Circle

Sorgenfrey Line is not a Moore Space

One way to get CCC spaces that are not separable

Some basic properties of spaces with countable chain condition