The evaluation map is a useful tool for embedding a space into a product space and plays an important role in many theorems and problems in topology. See here for a previous discussion. In this post, we present the evaluation map with the perspective that the map can be used for embedding a space into a function space of continuous functions. This post will be useful background for subsequent posts on 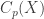 . In this post, we take a leisurely approach in setting up the scene. Once the map is defined properly, we show what additional conditions will make the evaluation map a homeomorphism. Then a function space perspective is presented as indicated above. After presenting an application, we conclude with some special cases for evaluation maps.
. In this post, we take a leisurely approach in setting up the scene. Once the map is defined properly, we show what additional conditions will make the evaluation map a homeomorphism. Then a function space perspective is presented as indicated above. After presenting an application, we conclude with some special cases for evaluation maps.
____________________________________________________________________
The general setting
Let  be a set (later we will add a topology). Let
be a set (later we will add a topology). Let  be a set of real-valued functions defined on
be a set of real-valued functions defined on  . Another way to view
. Another way to view  is that it is a subspace of the product space
is that it is a subspace of the product space 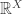 . For each
. For each 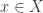 , consider the map
, consider the map 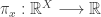 defined by
defined by 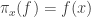 for all
for all  . One way to look at
. One way to look at  is that it is the projection map from the product space
is that it is the projection map from the product space 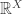 to one of the factors. Thus
to one of the factors. Thus  is continuous when
is continuous when 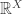 has the product topology. In fact, the product topology is the smallest topology that can be defined on
has the product topology. In fact, the product topology is the smallest topology that can be defined on 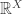 that would make the
that would make the  continuous. When we restrict the map
continuous. When we restrict the map  to the subspace
to the subspace  , the map
, the map  is still continuous.
is still continuous.
One more comment before defining the evaluation map. The set  of functions is a subspace of the product space
of functions is a subspace of the product space 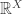 . Therefore the set
. Therefore the set  inherits the subspace topology from the product space. It makes sense to consider the function space
inherits the subspace topology from the product space. It makes sense to consider the function space  , the space of all continuous real-valued functions defined on
, the space of all continuous real-valued functions defined on  endowed with the pointwise convergence topology. Thus we can write
endowed with the pointwise convergence topology. Thus we can write  .
.
We now define the evaluation map. Define the map  by letting
by letting 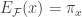 for each
for each 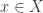 , or more explicitly, by letting, for each
, or more explicitly, by letting, for each 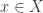 ,
,  be the map such that
be the map such that  for all
for all  .
.
The map 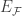 is called the evaluation map defined by the family
is called the evaluation map defined by the family  . When the set
. When the set  is understood, we can omit the subscript and denote the evaluation map by
is understood, we can omit the subscript and denote the evaluation map by  . We say
. We say 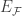 is the canonical evaluation map.
is the canonical evaluation map.
____________________________________________________________________
What makes the evaluation map works
The goal of the evaluation map is that it be a homeomorphism. For that to happen, we need to make a few more additional assumptions. In defining the evaluation map above, the functions in the family  are not required to be continuous. In fact, the set
are not required to be continuous. In fact, the set  is just a set in the above section. Now we require that
is just a set in the above section. Now we require that  is a topological space (it must be a completely regular space) and that all functions in
is a topological space (it must be a completely regular space) and that all functions in  are continuous. Thus we have
are continuous. Thus we have 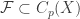 . With this assumption, the evaluation map is then a continuous function. We have the following theorem.
. With this assumption, the evaluation map is then a continuous function. We have the following theorem.
Theorem 1
Let  be a space. Let
be a space. Let 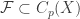 . Then the evaluation map
. Then the evaluation map  is always continuous.
is always continuous.
Proof of Theorem 1
Let 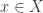 . Let
. Let  be open in
be open in  with
with 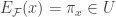 such that
such that
where 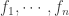 are arbitrary points of
are arbitrary points of  and each
and each 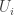 is an open interval of
is an open interval of 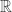 . For each
. For each 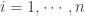 ,
, 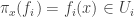 . Let
. Let 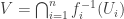 , which is open in
, which is open in  since each
since each 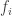 is a continuous function. We show that
is a continuous function. We show that 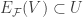 . For each
. For each  and for each
and for each 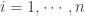 ,
,  . This means that for each
. This means that for each  ,
, 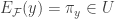 . The continuity of the evaluation map is established.
. The continuity of the evaluation map is established. 
In order to make the evaluation map a homeomorphism, we consider two more definitions. A family 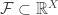 is said to separate points of
is said to separate points of  if for any
if for any 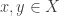 with
with  , there exists an
, there exists an  such that
such that 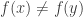 . A family
. A family 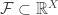 is said to separate points from closed subsets of
is said to separate points from closed subsets of  if for each
if for each 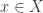 and for each closed subset
and for each closed subset  of
of  with
with 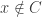 , there exists an
, there exists an  such that
such that 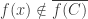 . We have the following theorem.
. We have the following theorem.
Theorem 2
Let  be a space. Let
be a space. Let 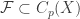 . Then the following are true about the evaluation map
. Then the following are true about the evaluation map  .
.
- If
 separates the points of
separates the points of  , then the evaluation map
, then the evaluation map  is a one-to-one.
is a one-to-one.
- If
 separates the points from closed subsets of
separates the points from closed subsets of  , then the evaluation map
, then the evaluation map  is a homeomorphism.
is a homeomorphism.
Proof of Theorem 2
To prove the bullet point 1, suppose that  separates the points of
separates the points of  . Let
. Let 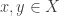 with
with  . Then there is some
. Then there is some  such that
such that 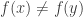 . It follows that the functions
. It follows that the functions 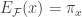 and
and 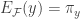 differ at the point
differ at the point  . This completes the proof for the bullet 1 of Theorem 2.
. This completes the proof for the bullet 1 of Theorem 2.
To prove the bullet point 2, suppose that the family  separates the points from closed subsets of
separates the points from closed subsets of  . It suffices to show that the evaluation map
. It suffices to show that the evaluation map 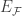 is an open map. Let
is an open map. Let 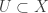 be a non-empty open set. We show that
be a non-empty open set. We show that 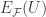 is open in image
is open in image  . Let
. Let 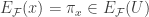 where
where 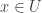 . Since
. Since  separates the points from closed subsets of
separates the points from closed subsets of  , there exists an
, there exists an  such that
such that 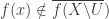 . Let
. Let 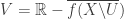 . Consider the following open set.
. Consider the following open set.
Clearly 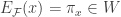 . We show that
. We show that 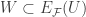 . Choose
. Choose 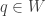 . Then
. Then 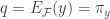 for some
for some  . It is also the case that
. It is also the case that  . Thus
. Thus  . This means that
. This means that 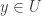 and that
and that 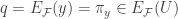 . This completes the proof for the bullet 2 of Theorem 2.
. This completes the proof for the bullet 2 of Theorem 2. 
____________________________________________________________________
Embedding every space into a function space
In defining the evaluation map, we start with a space  . Then take a family of continuous maps
. Then take a family of continuous maps 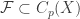 . As long as the family of functions
. As long as the family of functions  separates points from closed sets, we know for sure that the evaluation map is a homeomorphism from
separates points from closed sets, we know for sure that the evaluation map is a homeomorphism from  into a subspace of
into a subspace of  . We now look at some choices for
. We now look at some choices for  . One is that
. One is that 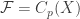 . Then we have the following corollary.
. Then we have the following corollary.
Corollary 3a
Any space  is homeomorphic to a subspace of the function space
is homeomorphic to a subspace of the function space  .
.
Because  is a completely regular space, the family
is a completely regular space, the family 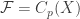 clearly separates points from closed sets. Thus Corollary 3a is valid. In fact, the complete regularity of
clearly separates points from closed sets. Thus Corollary 3a is valid. In fact, the complete regularity of  only requires that we use
only requires that we use  , the set of all continuous functions from
, the set of all continuous functions from  into
into  where
where ![I=[0,1]](https://s0.wp.com/latex.php?latex=I%3D%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) . We have the following corollary.
. We have the following corollary.
Corollary 3b
Any space  is homeomorphic to a subspace of the function space
is homeomorphic to a subspace of the function space 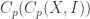 .
.
We can also let 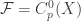 , the set of all bounded real-valued continuous functions defined on
, the set of all bounded real-valued continuous functions defined on  . It is clear that
. It is clear that  separates points from closed sets. So we also have:
separates points from closed sets. So we also have:
Corollary 3c
Any space  is homeomorphic to a subspace of the function space
is homeomorphic to a subspace of the function space  .
.
____________________________________________________________________
One application
We demonstrate one application of Corollary 3a. When  is a separable metric space,
is a separable metric space, 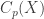 has a countable network (see this previous post). It is natural to ask whether every space with a countable network can be embedded in a
has a countable network (see this previous post). It is natural to ask whether every space with a countable network can be embedded in a  for some separable metric space
for some separable metric space  ? The answer is yes. We have the following theorem. One direction of the theorem is Theorem III.1.13 in [1].
? The answer is yes. We have the following theorem. One direction of the theorem is Theorem III.1.13 in [1].
Theorem 4
Let  be a space. Then the following conditions are equivalent.
be a space. Then the following conditions are equivalent.
- The space
 has a countable network.
has a countable network.
- The space
 can be embedded in a
can be embedded in a  for some separable metric space
for some separable metric space  .
.
Proof of Theorem 4
The direction  is clear. As shown here,
is clear. As shown here,  has a countable network whenever
has a countable network whenever  has a countable base. Having a countable network carries over to subspaces. The direction
has a countable base. Having a countable network carries over to subspaces. The direction  is the one that uses evaluation map.
is the one that uses evaluation map.

Suppose that 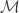 is a countable network for
is a countable network for  . Then
. Then 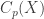 has a countable network, e.g., the set of all
has a countable network, e.g., the set of all ![[M,V]](https://s0.wp.com/latex.php?latex=%5BM%2CV%5D&bg=ffffff&fg=333333&s=0&c=20201002) where
where  ,
,  is any open interval with rational endpoints and
is any open interval with rational endpoints and ![[M,V]](https://s0.wp.com/latex.php?latex=%5BM%2CV%5D&bg=ffffff&fg=333333&s=0&c=20201002) is the set of all
is the set of all 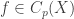 such that
such that  .
.
Any space with a countable network is the continuous image of a separable metric space. Thus there exists a separable metric space  such that
such that 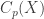 is the continuous image of
is the continuous image of  . Let
. Let 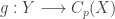 be a continuous surjection. Then
be a continuous surjection. Then  can be embedded into
can be embedded into  . The embedding
. The embedding 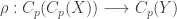 is defined by
is defined by 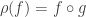 .
.
By Corollary 3a,  is embedded into
is embedded into  . Then
. Then  is embedded into
is embedded into  .
. 
____________________________________________________________________
More on the evaluation map
In this section, we consider some special cases. As shown in Theorem 2, what makes the evaluation map a one-to-one map is that the family 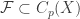 separates points of
separates points of  (for short, the family is point separating). What makes the evaluation map a homeomorphism is that the family
(for short, the family is point separating). What makes the evaluation map a homeomorphism is that the family  separates points from closed subsets of
separates points from closed subsets of  . In this section, we present one property that implies the property of separating points from closed sets. It is clear that if
. In this section, we present one property that implies the property of separating points from closed sets. It is clear that if  is dense in
is dense in 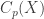 , then
, then  separates points of
separates points of  . In general, the fact that
. In general, the fact that  is point separating does not mean it separates point from closed sets. We show that whenever
is point separating does not mean it separates point from closed sets. We show that whenever  is compact, the fact that
is compact, the fact that  is dense in
is dense in 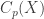 does imply that
does imply that  separates points from closed sets.
separates points from closed sets.
The family 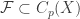 is said to be a generating set of functions if it determines the topology of
is said to be a generating set of functions if it determines the topology of  , i.e., the following set is a base for the topology of
, i.e., the following set is a base for the topology of  .
.
Since  is assumed to be a completely regular space, we observe that if
is assumed to be a completely regular space, we observe that if  is a base for
is a base for  , then the family
, then the family  separates points from closed subsets of
separates points from closed subsets of  . The following theorem captures the observations we make.
. The following theorem captures the observations we make.
Theorem 5
Let  be a space. Let
be a space. Let 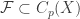 . Then if
. Then if  is a generating set of functions, then
is a generating set of functions, then  separates points from closed subsets of
separates points from closed subsets of  , hence the evaluation map
, hence the evaluation map  as defined above is a homeomorphism.
as defined above is a homeomorphism.
We now show that if  is compact and if
is compact and if  is dense in
is dense in 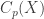 , then
, then  separates points from closed subsets of
separates points from closed subsets of  , making the evaluation map a homeomorphism.
, making the evaluation map a homeomorphism.
First one definition. Let  be a space. For any finite
be a space. For any finite  consisting of functions in
consisting of functions in 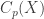 , define the maximum of
, define the maximum of  to be the function
to be the function 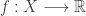 such that for each
such that for each 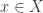 ,
, 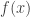 is the maximum of the real values in
is the maximum of the real values in 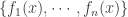 . In other words, the maximum of
. In other words, the maximum of  is the pointwise maximum of the functions in
is the pointwise maximum of the functions in  . It is not too difficult to show that the pointwise maximum of finitely many continuous real-valued functions is also continuous. We have the following lemma and corollary.
. It is not too difficult to show that the pointwise maximum of finitely many continuous real-valued functions is also continuous. We have the following lemma and corollary.
Lemma 6
Let the space  be compact. Suppose the family
be compact. Suppose the family  is dense in
is dense in 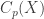 such that the pointwise maximum of any finite set of functions in
such that the pointwise maximum of any finite set of functions in  is also in
is also in  . Then
. Then  separates points from closed subsets of
separates points from closed subsets of  .
.
Proof of Lemma 6
Let 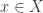 and let
and let  be a closed subset of
be a closed subset of  such that
such that 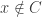 . For each
. For each 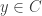 , consider the open set:
, consider the open set:
where 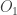 is the open interval
is the open interval 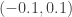 and
and  is the open interval
is the open interval 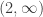 . For each
. For each 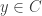 , choose
, choose  . The set of all
. The set of all 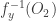 is an open cover of the compact set
is an open cover of the compact set  . Choose
. Choose 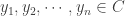 such that
such that 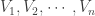 cover
cover  where each
where each 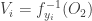 . Let
. Let 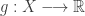 be the pointwise maximum of
be the pointwise maximum of 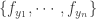 . By assumption,
. By assumption, 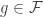 . It is clear that for all
. It is clear that for all 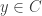 ,
, 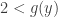 . Thus
. Thus 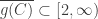 .
.
Let 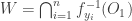 . It is also clear that
. It is also clear that  for all
for all  , implying
, implying  . Thus
. Thus  . Thus completes the proof that
. Thus completes the proof that  separates points from closed subsets of
separates points from closed subsets of  .
. 
Corollary 7
Let the space  be compact. If
be compact. If  is a dense subspace of
is a dense subspace of 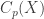 , then the evaluation map
, then the evaluation map  as defined above is a one-to-one map.
as defined above is a one-to-one map.
In Corollary 7, even if  is not closed under taking pointwise maximum of finitely many functions, then throw all pointwise maxima of all finite subsets of
is not closed under taking pointwise maximum of finitely many functions, then throw all pointwise maxima of all finite subsets of  into
into  and then apply Lemma 6. Throwing in all pointwise maxima will not increase the cardinality of
and then apply Lemma 6. Throwing in all pointwise maxima will not increase the cardinality of  . For example, suppose that
. For example, suppose that  is compact,
is compact, 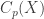 is separable and
is separable and  is a countable dense subspace of
is a countable dense subspace of 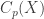 . Even if
. Even if  does not contain all the pointwise maxima of finite subspaces, we can then throw in all pointwise maxima and the subspace
does not contain all the pointwise maxima of finite subspaces, we can then throw in all pointwise maxima and the subspace  is still countable. Then the compact space
is still countable. Then the compact space  is homeomorphic to a subspace of
is homeomorphic to a subspace of  . Since
. Since  ,
,  is separable and metrizable. Thus the compact space
is separable and metrizable. Thus the compact space  is separable and metrizable. The following corollary captures this observation.
is separable and metrizable. The following corollary captures this observation.
Corollary 8
If  is a compact space and the function space
is a compact space and the function space 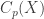 is separable, then
is separable, then  is metrizable.
is metrizable.
____________________________________________________________________
Reference
- Arkhangelskii, A. V., Topological Function Spaces, Mathematics and Its Applications Series, Kluwer Academic Publishers, Dordrecht, 1992.
____________________________________________________________________

be the first uncountable ordinal, and let
be the successor ordinal to
. Furthermore consider these ordinals as topological spaces endowed with the order topology. It is a well known fact that any continuous real-valued function
defined on either
or
is eventually constant, i.e., there exists some
such that the function
is constant on the ordinals beyond
. Now consider the function spaces
and
. Thus individually, elements of these two function spaces appear identical. Any
matches a function
where
is the result of adding the point
to
where
is the eventual constant real value of
. This fact may give the impression that the function spaces
and
are identical topologically. The goal in this post is to demonstrate that this is not the case. We compare the two function spaces with respect to some convergence properties (countably tightness and Frechet-Urysohn property) as well as normality.
and
is that of tightness. The function space
is countably tight, while
is not countably tight.
be a space. The tightness of
, denoted by
, is the least infinite cardinal
such that for any
and for any
with
, there exists
for which
and
. When
, we say that
has countable tightness or is countably tight. When
, we say that
has uncountable tightness or is uncountably tight.
is greater than
. For each
, define
such that
for all
and
for all
. Let
be the function that is identically zero. Then
where
is defined by
. It is clear that for any countable
,
. Thus
cannot be countably tight.
is a compact space. The fact that
is countably tight follows from the following theorem.
be a completely regular space. Then the function space
is countably tight if and only if
is Lindelof for each
.
.
has a property that is stronger than countable tightness. The function space
is a Frechet-Urysohn space (see this previous post). Of course,
not being countably tight means that it is not a Frechet-Urysohn space.
is not normal. If
is normal, then
would have countable extent. However, there exists an uncountable closed and discrete subset of
(see this previous post). On the other hand,
is Lindelof. The fact that
is Lindelof is highly non-trivial and follows from [2]. The author in [2] showed that if
is a space consisting of ordinals such that
is first countable and countably compact, then
is Lindelof.
and
are very different topologically. However, one of them can be embedded into the other one. The space
is the continuous image of
. Let
be a continuous surjection. Define a map
by letting
. It is shown in this previous post that
is a homeomorphism. Thus
is homeomorphic to the image
in
. The map
is also defined in this previous post.
tells us that the function space
, though Lindelof, is not hereditarily normal.
cannot be embedded in
. Note that
is countably tight, which is a hereditary property.
is associated with
which is obtained by appending the point
to
where
is the eventual constant real value of
. It may be tempting to think of the mapping
as a candidate for a homeomorphism between the two function spaces. The discussion in this post shows that this particular map is not a homeomorphism. In fact, no other one-to-one map from one of these function spaces onto the other function space can be a homeomorphism.
‘s, Comment. Math. Univ. Carolinae, 45 (1), 145-151, 2004.
